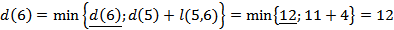В задаче необходимо найти кратчайшие расстояния по сети от каждой точки ко всем остальным.
Алгоритм Дейкстры.
1. Рассматриваем исходную вершину 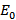 . Принимаем её в качестве текущей
. Принимаем её в качестве текущей 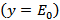 , начиная с которой будем производить расчёты кратчайших расстояний ко всем остальным вершинам сети. Расстояние к данной вершине принимаем равным нулю:
, начиная с которой будем производить расчёты кратчайших расстояний ко всем остальным вершинам сети. Расстояние к данной вершине принимаем равным нулю: 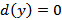 . Расстояния ко всем остальным вершинам равны
. Расстояния ко всем остальным вершинам равны 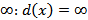 .
.
2. Используя формулу: 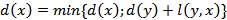 , где
, где 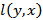 - расстояние от текущей вершины
- расстояние от текущей вершины 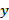 к заданной
к заданной 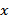 , находим кратчайшие расстояния ко всем вершинам от текущей, взятой в качестве исходной на данном этапе расчётов.
, находим кратчайшие расстояния ко всем вершинам от текущей, взятой в качестве исходной на данном этапе расчётов.
Если между вершинами нет связи, то соответствующие 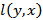 принимаем равными бесконечности
принимаем равными бесконечности 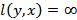 .
.
3. Среди найденных значений 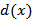 выбираем наименьшее и соответствующую вершину
выбираем наименьшее и соответствующую вершину 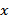 принимаем в качестве текущей:
принимаем в качестве текущей: 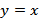 . Минимальное расстояние к новой текущей вершине от исходной принимаем равным
. Минимальное расстояние к новой текущей вершине от исходной принимаем равным 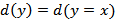 .
.
4. Проверяем условие 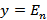 , где
, где 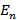 - завершающая сеть. Если условие выполняется, то расчёт окончен, если нет, то возвращаемся к шагу 2, и процесс решения продолжается.
- завершающая сеть. Если условие выполняется, то расчёт окончен, если нет, то возвращаемся к шагу 2, и процесс решения продолжается.
На каждой итерации вершина, к которой было найдено кратчайшее расстояние, выделяется на сети. Выделяется также ребро, соответствующее данному кратчайшему расстоянию.
Для иллюстрации алгоритма рассмотрим пример.
Пусть задана сеть
Для данной сети необходимо найти кратчайшее расстояние от вершины 1 к вершине 6, а также ко всем остальным.
Решение
1) Выбираем в качестве текущей вершины исходную 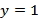 . Кратчайшее расстояние до данной вершины равно нулю
. Кратчайшее расстояние до данной вершины равно нулю 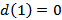 . К остальным вершинам кратчайшие расстояния от текущей ещё не найдены. Принимаем их равными бесконечности
. К остальным вершинам кратчайшие расстояния от текущей ещё не найдены. Принимаем их равными бесконечности 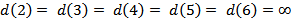 .
.
2) Рассчитываем кратчайшие расстояния от текущей вершины 1 к вершинам 2, 3, 4, 5 и 6, используя формулу 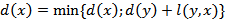
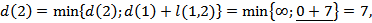
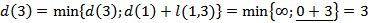
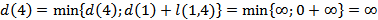
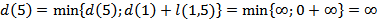
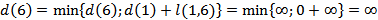
3) Выбираем наименьшую из полученных величин
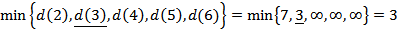
Вершина 3 принимается в качестве новой текущей вершины, то есть 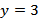 . Она будет теперь рассматриваться как отправная точка для расчёта кратчайших расстояний от исходной к оставшимся вершинам: 2, 4, 5 и 6.
. Она будет теперь рассматриваться как отправная точка для расчёта кратчайших расстояний от исходной к оставшимся вершинам: 2, 4, 5 и 6.
Выделяем на сети вершину 3 и ребро, соединяющее исходную вершину с данной
4) Проверяем условие 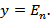 Так как вершина 3 не является завершающей (3¹6), то возвращаемся к шагу 2.
Так как вершина 3 не является завершающей (3¹6), то возвращаемся к шагу 2.
Дальнейшие расчёты произведём без обозначения номера шага.
Рассчитываем кратчайшие расстояния от исходной вершины к вершине 2, 4, 5 и 6, рассматривая в качестве текущей вершину 3
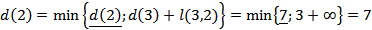
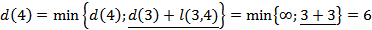
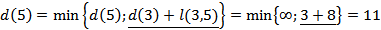
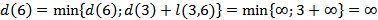
Выбираем наименьшую из полученных вершин
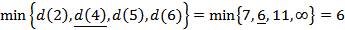
Вершина 4 становится новой текущей вершиной 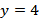 и
и 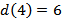 .
.
Выделяем на сети вершину 4 и ребро (3,4)
Проверяем условие 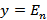 . Так как вершина 4 не является завершающей (4¹6), то повторяем расчёты.
. Так как вершина 4 не является завершающей (4¹6), то повторяем расчёты.
Рассчитываем кратчайшие расстояния от исходной вершины к вершинам 2, 5 и 6, рассматривая в качестве текущей вершину 4
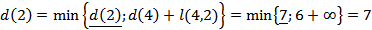
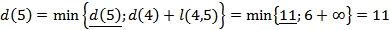
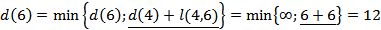
Выбираем наименьшую из полученных величин
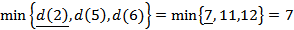
Вершина 2 становится новой текущей вершиной 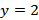 и
и 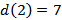 .
.
Выделяем на сети вершину 2 и ребро (1,2)
Проверяем условие 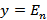 . Вершина 2 не является завершающей (2¹6), поэтому продолжаем расчёты.
. Вершина 2 не является завершающей (2¹6), поэтому продолжаем расчёты.
Рассчитываем кратчайшие расстояния от исходной вершины к вершинам 5 и 6, рассматривая в качестве текущей вершину 2
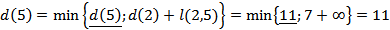
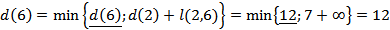
Выбираем наименьшую из полученных величин
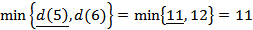
В качестве текущей выбирается вершина 5 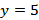 и
и 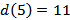 .
.
Выделяем на сети вершину 5 и ребро (3,5)
Остаётся произвести расчёты для вершины 6
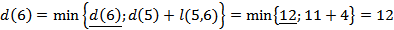
Итак, кратчайшее расстояние от исходной вершины 1 к завершающей 6 составляет 12 единиц.
Выделяем вершину 6 и дугу (4,6)
Результаты расчётов сведены в таблицу
| Вершина
| Кратчайшее расстояние
| Путь
|
| 2
| 7
| 1 – 2
|
| 3
| 3
| 1 – 3
|
| 4
| 6
| 1 – 3 – 4
|
| 5
| 11
| 1 – 3 – 5
|
| 6
| 12
| 1 – 3 – 4 – 6
|
3. Потоки в сетях.
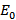 . Принимаем её в качестве текущей
. Принимаем её в качестве текущей 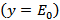 , начиная с которой будем производить расчёты кратчайших расстояний ко всем остальным вершинам сети. Расстояние к данной вершине принимаем равным нулю:
, начиная с которой будем производить расчёты кратчайших расстояний ко всем остальным вершинам сети. Расстояние к данной вершине принимаем равным нулю: 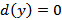 . Расстояния ко всем остальным вершинам равны
. Расстояния ко всем остальным вершинам равны 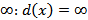 .
.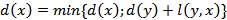 , где
, где 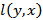 - расстояние от текущей вершины
- расстояние от текущей вершины 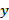 к заданной
к заданной 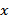 , находим кратчайшие расстояния ко всем вершинам от текущей, взятой в качестве исходной на данном этапе расчётов.
, находим кратчайшие расстояния ко всем вершинам от текущей, взятой в качестве исходной на данном этапе расчётов.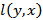 принимаем равными бесконечности
принимаем равными бесконечности 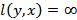 .
.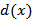 выбираем наименьшее и соответствующую вершину
выбираем наименьшее и соответствующую вершину 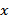 принимаем в качестве текущей:
принимаем в качестве текущей: 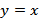 . Минимальное расстояние к новой текущей вершине от исходной принимаем равным
. Минимальное расстояние к новой текущей вершине от исходной принимаем равным 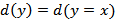 .
.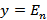 , где
, где 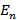 - завершающая сеть. Если условие выполняется, то расчёт окончен, если нет, то возвращаемся к шагу 2, и процесс решения продолжается.
- завершающая сеть. Если условие выполняется, то расчёт окончен, если нет, то возвращаемся к шагу 2, и процесс решения продолжается.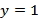 . Кратчайшее расстояние до данной вершины равно нулю
. Кратчайшее расстояние до данной вершины равно нулю 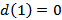 . К остальным вершинам кратчайшие расстояния от текущей ещё не найдены. Принимаем их равными бесконечности
. К остальным вершинам кратчайшие расстояния от текущей ещё не найдены. Принимаем их равными бесконечности 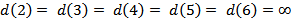 .
.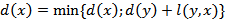
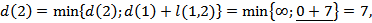
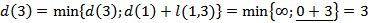
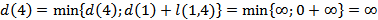
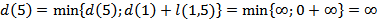
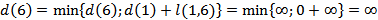
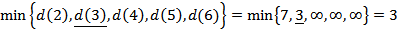
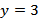 . Она будет теперь рассматриваться как отправная точка для расчёта кратчайших расстояний от исходной к оставшимся вершинам: 2, 4, 5 и 6.
. Она будет теперь рассматриваться как отправная точка для расчёта кратчайших расстояний от исходной к оставшимся вершинам: 2, 4, 5 и 6.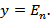 Так как вершина 3 не является завершающей (3¹6), то возвращаемся к шагу 2.
Так как вершина 3 не является завершающей (3¹6), то возвращаемся к шагу 2.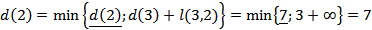
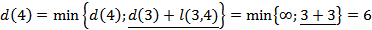
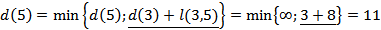
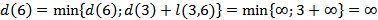
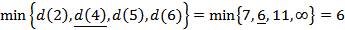
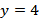 и
и 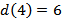 .
.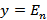 . Так как вершина 4 не является завершающей (4¹6), то повторяем расчёты.
. Так как вершина 4 не является завершающей (4¹6), то повторяем расчёты.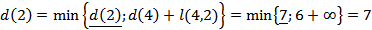
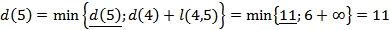
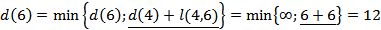
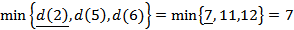
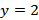 и
и 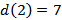 .
.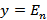 . Вершина 2 не является завершающей (2¹6), поэтому продолжаем расчёты.
. Вершина 2 не является завершающей (2¹6), поэтому продолжаем расчёты.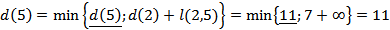
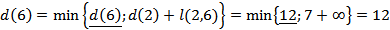
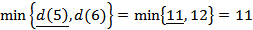
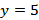 и
и 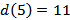 .
.