Математически конечным графом ( G ) называется пара , где – непустое конечное множество вершин, а – конечное (возможно пустое) множество дуг или рёбер. Обозначается граф через .
ПЛАН ЗАНЯТИЯ
Дисциплина: ОП.10 Математические методы
Преподаватель: Старченко Е.А
Курс: 3
Группа: 1 ПКС-20
Специальность: Программирование в компьютерных системах
Дата: 14.12.22
Время проведения: 13-30 – 15-00, 4 пара
Тема: Основные понятия теории графов. Кратчайший путь на графе.
Цель занятия:
дидактическая: познакомиться с основными понятиями теории игр; методами определения кратчайшего пути на графе;
развивающая: развивать логическое мышление, внимание
Вид занятия лекция
Литература
Ходыкин В.Ф., ПреображенскийА.А. Сборник задач по математическому программированию, стр. 108
Интернет-ресурсы:
видео https://youtu.be/4TscCFj3REk
Задание: законспектировать лекцию и ответить на вопросы. Убедительная просьба писать аккуратно и разборчиво, страницы нумеровать. Ответы в электронном варианте отправить в личные сообщения для проверки
КОНСПЕКТ ЛЕКЦИИ
1. Основные понятия теории графов.
2. Кратчайший путь на графе. Алгоритм Дейкстры.
3. Потоки в сетях.
1. Основные понятия теории графов.
Задачи на сетях представляют собой один из довольно часто применяемых в практике разделов исследования операций. Среди сетевых задач могут быть рассмотрены как детерминированные, так и задачи с вероятностными характеристиками. Элементы теории графов рассматриваются в данной теме в качестве основы методов сетевого моделирования.
Понятие графа исключительно наглядно: это совокупность точек, соединённых линиями. В теории ещё не сложились чёткие определения и стандарты, поэтому в некоторых источниках граф называют сетью.
| Еi |
Существуют принятые обозначения вершин и рёбер, изображённые ниже.
Обозначение вершин
Обозначения рёбер
Рассмотрим геометрическое изображение графа:
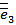
|
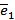
|
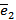
|
| Е2 |
| Е3 |
| Е1 |
или
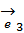
|
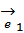
|
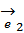
|
| Е2 |
| Е3 |
| Е1 |
и дадим его определение с математической точки зрения.
Математически конечным графом ( G ) называется пара 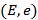 , где
, где 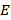 – непустое конечное множество вершин, а
– непустое конечное множество вершин, а 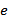 – конечное (возможно пустое) множество дуг или рёбер.
– конечное (возможно пустое) множество дуг или рёбер.
Обозначается граф через 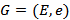 .
.
Частными случаями являются:
а) нуль-граф (множество 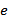 – пустое)
– пустое)
| Е2 |
| Е3 |
| Е1 |
б) полный граф (все вершины связаны между собой)
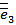
|
|
|
| Е2 |
| Е3 |
| Е1 |
Дугой называется ориентированная пара 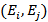 вершин, где
вершин, где 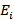 – начальная вершина дуги, а
– начальная вершина дуги, а 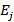 – конечная. Дуга на графе всегда имеет стрелку, которая показывает порядок вершин и обозначается буквой с индексом
– конечная. Дуга на графе всегда имеет стрелку, которая показывает порядок вершин и обозначается буквой с индексом 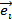 .
.
Дуга вида 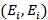 называется петлёй.
называется петлёй.
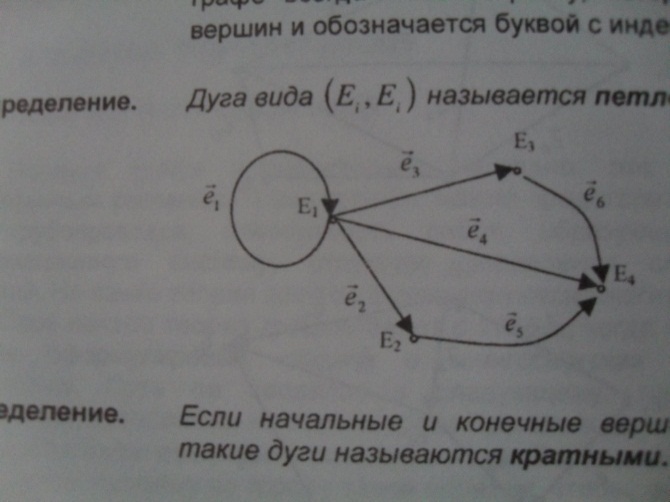
Иногда две дуги с одинаковыми вершинами, но противоположной ориентацией объединяют. Данное объединение называют ребром.
Неориентированная пара 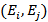 вершин графа называется ребром и обозначается
вершин графа называется ребром и обозначается 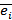 или
или 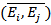 .
.
Если две дуги или ребра имеют хотя бы одну общую вершину, то они называются смежными.
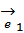
|
|
| Е2 |
| Е3 |
| Е1 |
Различают три типа графов:
- ориентированный;
- неориентированный;
- смешанный.
Если все связи между вершинами графа заданы дугами, то такой граф называется ориентированным (или орграфом).
Орграф обозначается 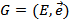 , где
, где 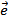 - множество дуг графа.
- множество дуг графа.
Неориентированный граф – граф, у которого все связи заданы рёбрами.
Орграф обозначается 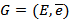 , где
, где 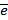 - множество рёбер графа.
- множество рёбер графа.
Смешанным называется граф, содержащий и дуги, и рёбра.
Концевые точки (вершины) ребра (дуги) называются смежными вершинами, при этом они инцидентны этому ребру (дуге), а ребро инцидентно (дуга инцидентна) вершинам.
| Е1 |
| Е2 |
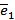
|
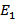 и
и 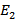 - смежные вершины.
- смежные вершины.
Путь – это конечная последовательность дуг 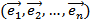 ,
, 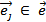 , у которой начало каждой последующей дуги совпадает с концом предыдущей.
, у которой начало каждой последующей дуги совпадает с концом предыдущей.
Записать путь можно, например, так: 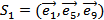 .
.
Путь имеют такую характеристику, как длина, которая равна числу дуг, входящих в путь.
2. Кратчайший путь на графе. Алгоритм Дейкстры.
Задача на нахождение кратчайших расстояний на заданной сети является одной из классических и наиболее часто применяемых сетевых задач. К их числу относятся задачи замены оборудования, определения срока службы машины, оптимальных маршрутов движения и другие. Решение данной задачи позволяет рассчитать затраты на доставку грузов для заданной сети, которые могут быть использованы при нахождении оптимальной схемы прикрепления поставщиков к потребителям и так далее.
Постановка задачи.
Имеется некоторая сеть 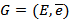 , все её связи между вершинами которой заданы рёбрами (хотя это и не обязательно, можно рассматривать и ориентированный граф). Пусть
, все её связи между вершинами которой заданы рёбрами (хотя это и не обязательно, можно рассматривать и ориентированный граф). Пусть 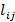 - длина ребра
- длина ребра 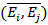 . Причём
. Причём 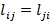 . Две точки
. Две точки 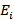 и
и 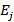 будем считать соседними (или смежными), если они соединены ребром.
будем считать соседними (или смежными), если они соединены ребром.








