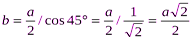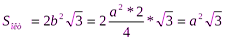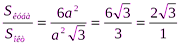ІІ. Повторение понятия правильного многогранника.
12. 05. 2022 .г. 10 класс. Геометрия.
Тема урока: « Правильные многогранники».
Цель:
· Закрепление учащимися определения правильного многогранника, свойств пяти типов правильных многогранников;
· формирование умений и навыков решения задач, связанных с правильным тетраэдром, октаэдром, кубом;
· способствовать развитию познавательной активности учащихся путем ознакомления с историей развития учения о правильных многогранниках, применением в современных научных теориях;
· содействовать в ходе урока формированию следующих мировоззренческих идей: познаваемости мира, движения, развития в природе и в обществе.
Методы: наглядные, практические.
Тип: урок закрепления знаний, умений, навыков.
І. Мотивация обучения.
Есть в школьной геометрии особые темы, которые ждешь с нетерпением, предвкушая встречу с невероятно красивым материалом. К таким темам можно отнести «Правильные многогранники». Здесь не только открывается удивительный мир геометрических тел, обладающих неповторимыми свойствами, но и интересные научные гипотезы. И тогда урок геометрии становится своеобразным исследованием неожиданных сторон привычного школьного предмета.
ІІ. Повторение понятия правильного многогранника.
Гексаэдр, Тетраэдр, Октаэдр, Додекаэдр, Икосаэдр.
ІІІ. Формирование умений и навыков решения задач.
Устное решение задач.
Задание 1. Решить анаграмму и исключить лишнее слово.
Примечание: слово «анаграмма» греческого происхождения и означает перестановку букв в слове, приводящую к другому слову.
у б к, р и а п м з,
т а р д э т е р, т о д а к р э,
д к а и с о р э, д е о д э к д а р
Ответ: куб, призма, тетраэдр, октаэдр, икосаэдр, додекаэдр. Лишнее слово – призма.
Об этих телах речь пойдет при решении задач.
Задачи.
1. Определить сумму плоских углов при вершине тетраэдра, октаэдра, икосаэдра.
(60 * 3 = 
; 
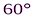* 4 = 
; 
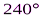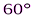* 5 = 
)
2. Площадь полной поверхности икосаэдра равна 480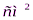 
. Найти площадь одной грани.
( 
)
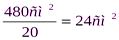3. Какая связь между понятиями правильная треугольная пирамида и правильный тетраэдр?
(правильный тетраэдр – частный случай правильной, треугольной пирамиды)
Задачи.
1. Найти сумму плоских углов при всех вершинах додекаэдра.
Указание: угол правильного пятиугольника вычисляем по формуле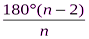 
, где n – число сторон.
(3* 
)
2. Длина ребра октаэдра равна 6 см. найти площадь его полной поверхности.
( 
)
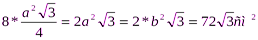3. Привести пример многогранника, все ребра которого равны, но который не был бы правильный.
(пирамида с равными ребрами, основанием которой служит квадрат).
Задачи.
1. Какие правильные многогранники имеют правильные плоские углы?
(тетраэдр, октаэдр, икосаэдр)
2. Поверхность додекаэдра 180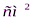 
. Определить площадь его грани.
(180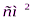 
/ 12 = 15 )
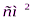3. Какие из правильных пирамид (призм) являются правильными многогранниками?
(правильный тетраэдр, куб)
Решение задач
Задача 1
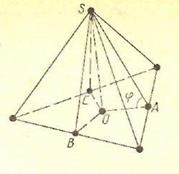Найдите двугранные углы правильного тетраэдра.
Решение:
Пусть искомый угол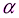 
(все шесть углов при ребрах правильного тетраэдра равны), из медианного сечения тетраэдра получается формула:
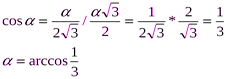
Задача 2.
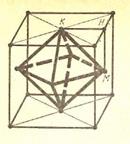Доказать, что центры граней куба являются вершинами октаэдра. Найдите отношение площадей их поверхностей.
Все отрезки, соединяющие центры двух соседних граней являются гипотенузами прямоугольных треугольников с катетами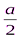 
, где а – ребро куба (на рисунке показан один такой треугольник - 
КМН), поэтому они равны и ограничивают восемь правильных треугольников. В каждом центре сходится по четыре таких треугольников и оба условия «правильности» выполнены S куба = 6 
ребро октаэдра 
