Итоговая контрольная работа по алгебре за курс 9 класс
Итоговая контрольная работа по алгебре за курс 9 класса составлена на основе учебника «Алгебра 9», Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И. и др. / Под ред. Теляковского С.А. с использованием открытого банка заданий ОГЭ по математике www.mathege.ru.
Работа составлена в двух вариантах. Каждый вариант работы состоит из двух частей. Часть I содержит задания базового уровня сложности по темам: "Неравенства", "Системы неравенств", "Функции. Квадратичная функция", "Прогрессии", "Теория вероятностей" оцениваются одним баллом. 2 часть содержит три задания повышенного и высокого уровней сложности. Каждое задание 2-й части оценивается 2 баллами .
Работа рассчитана на 1 урок (40 минут).
Критерии оценивания:
Всего можно набрать 15 баллов. «2» -0-4балла ; «3»- 5-9 баллов; «4»- 10-12 баллов; «5» - 13-15 баллов.
Вариант 1
Часть I
1.(4б) Решите неравенства:
а) 7 - 2x > 9; б) х2 - 6х + 8 > 0;
в) х² < 4; г) (х – 3)(х – 1) ≤ 0.
2.(1б) Решите систему неравенств:
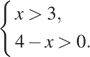
3.(1б) На каком из рисунков изображен график квадратичной функции?
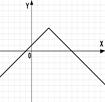
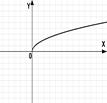
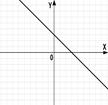
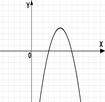
1); 2) ;3) ;4).
4. (1б)Дана арифметическая прогрессия: -4; -2; 0; … Найдите десятый её член.
5.(1б) Найдите сумму пяти первых членов геометрической прогрессии (bn), если b1= – 1, а q= – 2.
6. (1б) На каждой грани куба написана одна из букв слова «ГРАФИК».
Какова вероятность того, что куб упадет на грань с согласной буквой?
Часть II
7.(2б) Решите уравнение 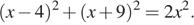
8. (2б) Дорога между пунктами A и В состоит из подъёма и спуска, а её длина равна 27 км.
Турист прошёл путь из А в В за 8 часов, из которых спуск занял 3 часа. С какой
скоростью турист шёл на спуске, если его скорость на подъёме меньше его скорости
на спуске на 1 км/ч?
9. (2б).Постройте график функции и определите, при каких значениях с прямая у = с имеет с графиком ровно две общие точки.
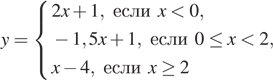
Вариант 2
Часть I
1. (4б)Решите неравенства: а) 3 - 3x < 12; б) 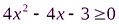 ;
;
в) х² < 9; г) (х – 2)(х – 4) < 0.
2.(1б) Решите систему неравенств:
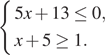
3.(1б) На каком из рисунков изображен график квадратичной функции?
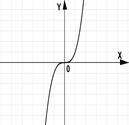
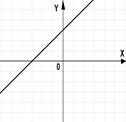
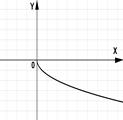
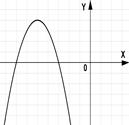
1); 2); 3); 4).
4.(1) Арифметическая прогрессия задана первыми двумя членами: а1 = 8, а2 = 5.
Найдите 16 член этой прогрессии.
5.(1б) Найдите сумму четырех первых членов геометрической прогрессии (bn),
если b1= – 1, а q = – 4.
6.(1б) На каждой грани куба написана одна из букв слова «ПРИЗМА».
Какова вероятность того, что куб упадет на грань с согласной буквой?
Часть II
7.(2б) Решите уравнение 
8.(2б) Два автомобиля одновременно отправляются в 240-километровый пробег. Первый едет со скоростью, на 20 км/ч большей, чем второй, и прибывает к финишу на 1 ч раньше второго. Найдите скорость первого автомобиля.
9.(2б) Постройте график функции и определите, при каких значениях m прямая y = m имеет с графиком ровно две общие точки.
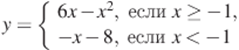
Ответы:
| № | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Ответ Вариант 1. | а)х<-1; б)x<2 X>4; в)-2<х<2; г)1<=х<=3 | 3<X<4 | 1 | 14 | -11 | 2\3 | -2,5 | 4км\ч | -2;1. |
| Вариант 1. | а)х>-3; б)x<-0,5 X>1,5; в)-3<х<3; г)2<x<4 | -4<=х<=-2,5 | 4 | -37 | 51 | 2\3 | 2,5 | 80км\ч | -7;9. |








