7 Моделирование и анализ зависимостей между качественными признаками
7.1 Анализ методов исследования качественных данных
Методы анализа качественных данных могут включать:
- факторный анализ - совокупность методов, которые позволяют выявлять латентные (скрытые, неявные) обобщающие характеристики структуры и механизма развития изучаемых явлений и процессов на основе существующих связей признаков (или объектов);
- кластерный анализ - методы, которые используются для классификации объектов или событий в относительно однородные группы, которые называют кластерами. То есть если данные понимать как точки в признаковом пространстве, то задача формулируется как выделение «сгущений точек», разбиение совокупности на однородные подмножества объектов, которые в каждом кластере должны быть похожи между собой и отличаться от других;
- дисперсионный анализ – метод, позволяющий исследовать влияние одной или несколько независимых переменных на одну зависимую переменную или на несколько зависимых переменных. В дисперсионном анализе исследователь исходит из предположения, что одни переменные выступают как влияющие (факторы, независимые переменные), а другие (результативные признаки, зависимые переменные) – подвержены влиянию этих факторов;
- многомерное шкалирование позволяет решить две основные задачи: получить обобщенную оценку исследуемой характеристики (а не ее отдельных аспектов), и определить, не навязывая собственного мнения респондентам, какими же признаками они руководствовались в процессе оценивания того или иного объекта исследования;
- анализ соответствий является достаточно гибким относительно вида исходных данных (это могут быть частотные данные, проценты, данные в виде рейтингов и т.д.) и обеспечивает наглядную картину взаимосвязи переменных и, таким образом, способствует возникновению новых идей и предположений относительно природы этих взаимосвязей, которые могут затем проверяться более тонкими и строгими методами анализа;
- дискриминантный анализ используется для разбиения образцов на группы с целью обнаружить общую структуру, исходя из набора измерений. Кроме того, данный метод также может быть использован для того, чтобы определить, какие переменные вносят вклад в эту классификацию;
- анализ временных рядов, например, в маркетинге, используется для прогнозирования спроса и его сезонных, циклических и случайных изменений. Он основывается на разбивке данных об объеме продаж в прошлом для прогнозирования спроса в будущем. Но существуют и более сложные модели прогноза, опирающиеся на анализ временных рядов. Например, можно ответить на вопрос, покупки каких товаров предшествуют покупке данного вида продукции. [6]
7.2 Логистическая регрессия
С помощью метода бинарной логистический регрессии можно исследовать зависимость переменных от независимых переменных, имеющий любой вид шкалы. Данный вид регрессии рассчитывает вероятность наступления события в зависимости от значений независимых переменных.
Вероятность наступления события для некоторого случая рассчитывается по формуле (4):
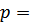
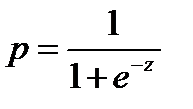, (4)
где 
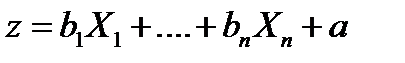, X 1
где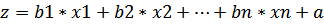 
где x 1 – значение независимых переменных,
b1 – коэффициенты, расчет которых является задачей бинарной логистической регрессии;
a - некоторая контакта.
Расчет коэффициентов b1,…bn производится алгоритмом Ньютона; целью расчета является получение такого набора коэффициентов, который обеспечит максимальное правдоподобен. [3]
Если для p получится значение меньшее 0,5, то можно предположить, что событие не наступит; в противном случае предполагается наступление
события. [5]
Задача: оценить вероятность того, что испытуемый образец перфоратора можно использовать как шуруповерт, если он может работать в режиме сверление.
Алгоритм построения бинарной логистической модели в ПАП «DEDUCTOR» содержит следующие шаги:
1 Шаг - выбираем на панели «Сценарии» выбираем обработчик «Логистическая регрессия».
2 Шаг – в отрывшемся окне выбираем входные и выходные параметры. В конкретном случае выбираем два номинальных значения:
- в качестве входного значения назначаем П15 – работа в режиме шуруповерт, где «1» означает возможность работы в этом режиме, «2» означает - невозможность
- в качестве выходного – П7 – режим работы сверление, где «1» означает возможность работы в этом режиме, «2» означает - невозможность.
Данные показатели имеют по 2 уникальных значения, что видно в правой части окна и является допустимым для построения логистической модели (рисунок 7.1).
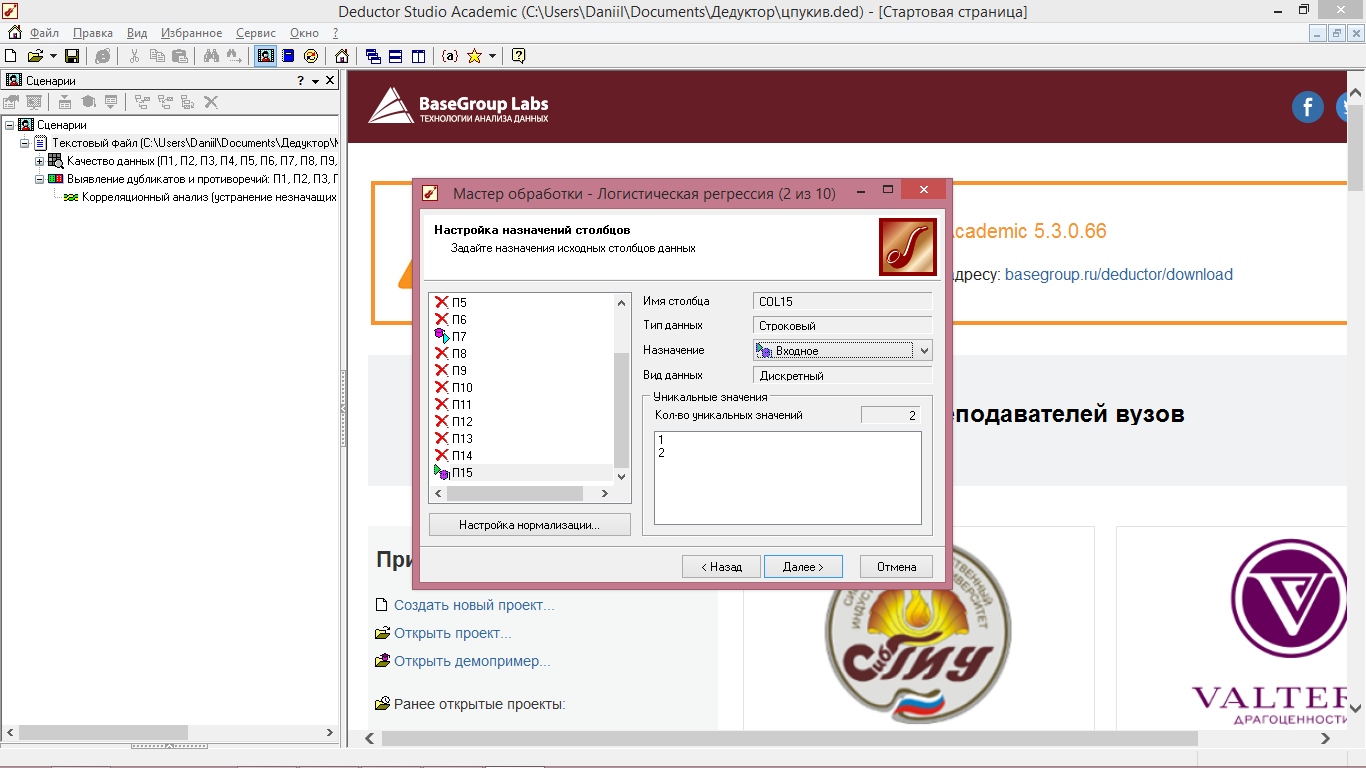
Рисунок 7.1 - Логистическая регрессия (назначение входных и выходных параметров)
3 Шаг – производим разбиение исходного набора данных на подмножества, нажимаем «Далее».
4 Шаг – производим настройку отбора переменных в регрессионные модели, выбираем «Полное значение (Enter)», обеспечивающее, что в модель будут включены все доступные переменные; нажимаем «Далее».
5 Шаг – устанавливаем значения параметров построения регрессионной модели (рисунок 7.2).
Установка флажка «Максимальное число итераций» позволяет задать число итераций численного алгоритма, по достижении которого расчет останавливается независимо от выполнения условия сходимости (точность функции оценки). [3] Автоматически устанавливается значение, равное 100.
«Точность функции оценки» означает, что алгоритм расчета коэффициентов завершится, когда очередное значение функции правдоподобия -2 Log likehood прекратит изменяться в пределах заданной точности. [3] Для конкретного примера 0,8542.
«Порог отсечения» изменяется в пределах от 0 до 1, при котором происходит классификация образца к одному из двух классов. [3]
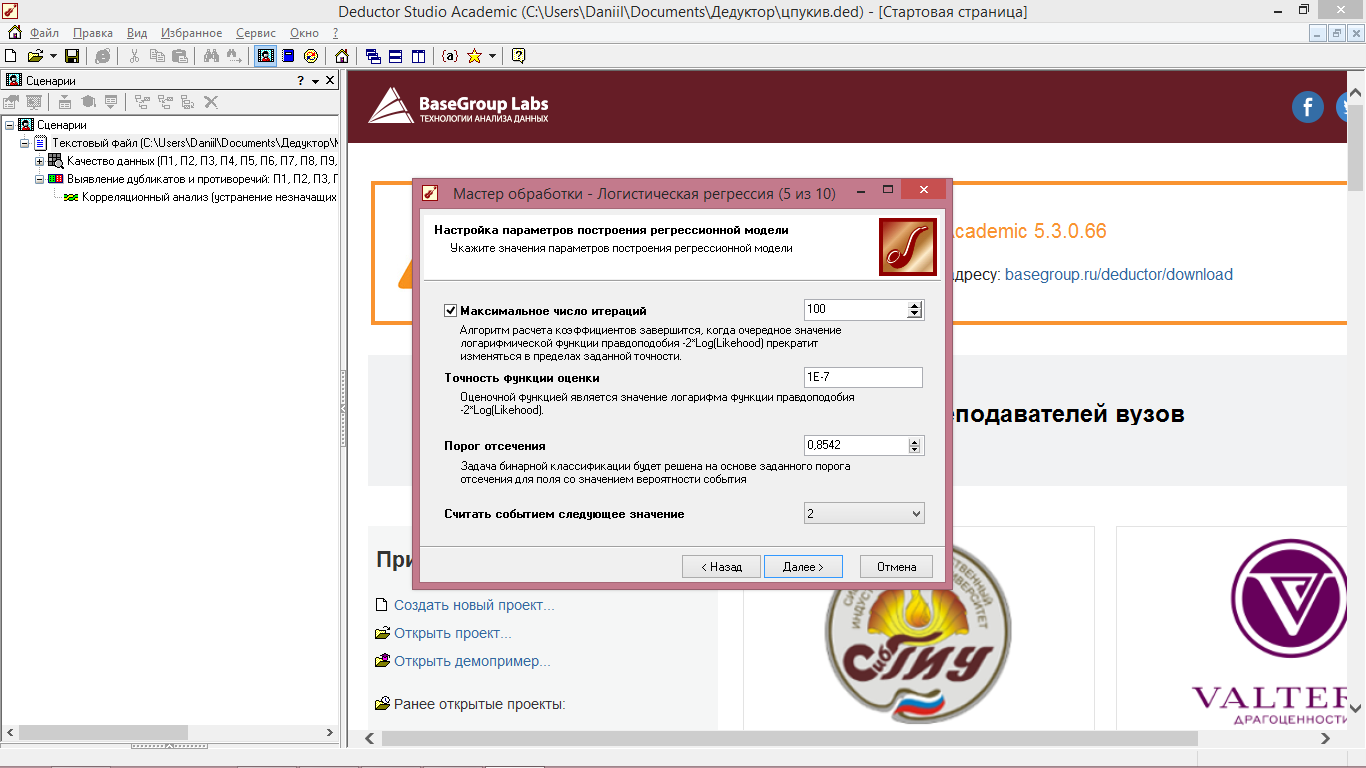
Рисунок 7.2 - Логистическая регрессия (настройка параметров регрессионной модели)
«Считать событием следующее значение» задает, какое из двух уникальных значений будет считаться событием. В конкретном случае устанавливаем «выдерживает», так как событием будет считаться то, что образец пройдет испытания на прозрачность.
6 Шаг – производим калибровку логрессионной модели, нажимаем «Далее» (рисунок 49).
Для этого выбираем «Определить из обучающего множества (модель не корректируется), то есть предполагается, что пропорции событий и не-событий в обучающей выборке соответствуют таковым в генеральной совокупности. [3]
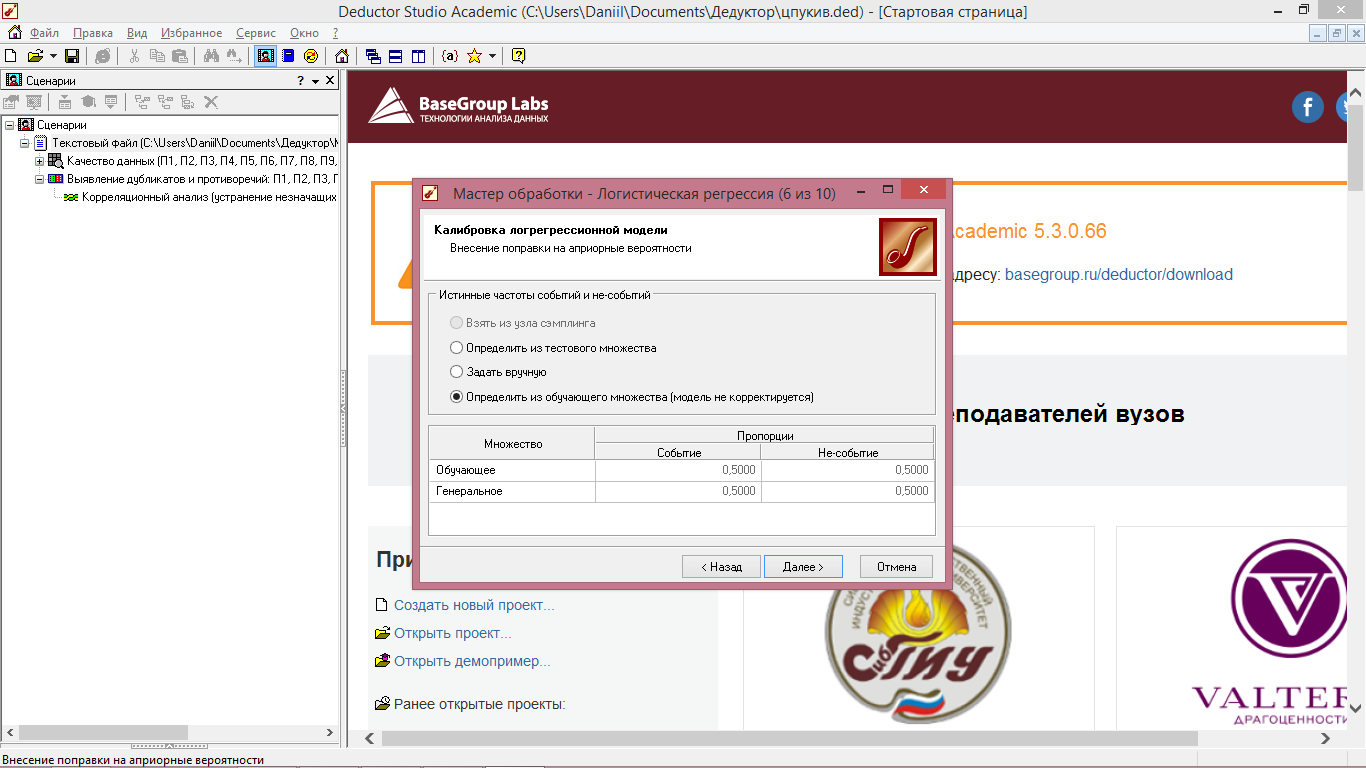
Рисунок 7.3 - Логистическая регрессия (калибровка логрессионной модели)
В окне мастера отображены пропорции событий и не-событий в обучающей выборке и генеральной совокупности. Исходя из этого, можно сделать вывод, что доля вероятности того, что образец имеющий режим «сверление» имеет режим «шуруповерт» составляет 0,8542, а доля вероятности того, что образец не имеет такой связи составляет 01458.
7 Шаг – производим преобразование отношения шансов в линейную шкалу баллов (рисунок 7.4). В результате данного этапа каждому отношению шансов в переменной регрессионного уравнения будет соответствовать определенное число баллов. [3]
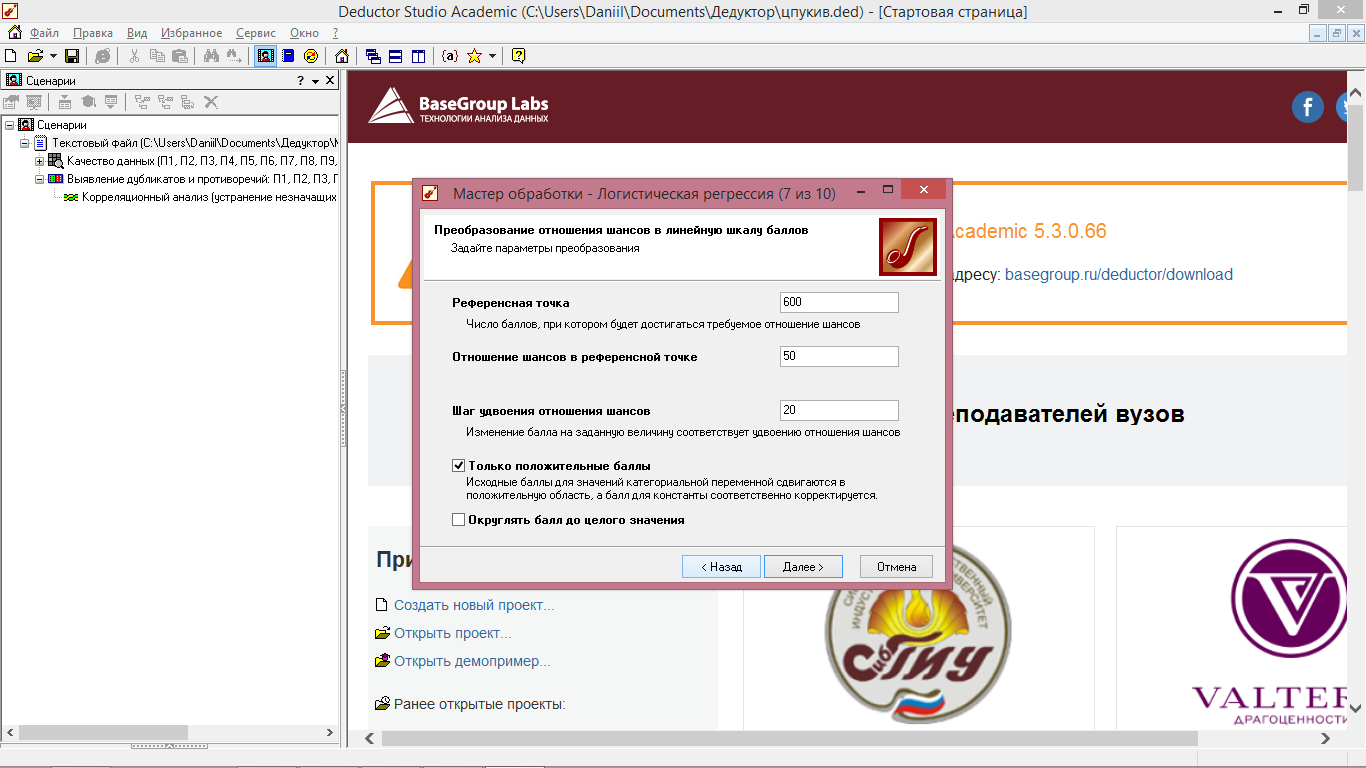
Рисунок 7.4- Логистическая регрессия
(преобразование отношения шансов в линейную шкалу баллов)
8 Шаг – запускаем процесс построения логистической модели, нажимаем «Далее».
9 Шаг – выбираем способы отображения данных (рисунок 7.5), вводим имя и метку, нажимаем «Готово».
Рисунок 7.5- Логистическая регрессия (выбор способа отображения данных)
Для анализа используем полученную таблицу сопряженности (рисунки 7.6, 7.7), в которой ячейки с числом правильно распознанных примеров отображаются в зеленых ячейках, а неправильно распознанные – в красных. Чем большее число примеров попало в зеленые ячейки, тем лучше результаты классификации.
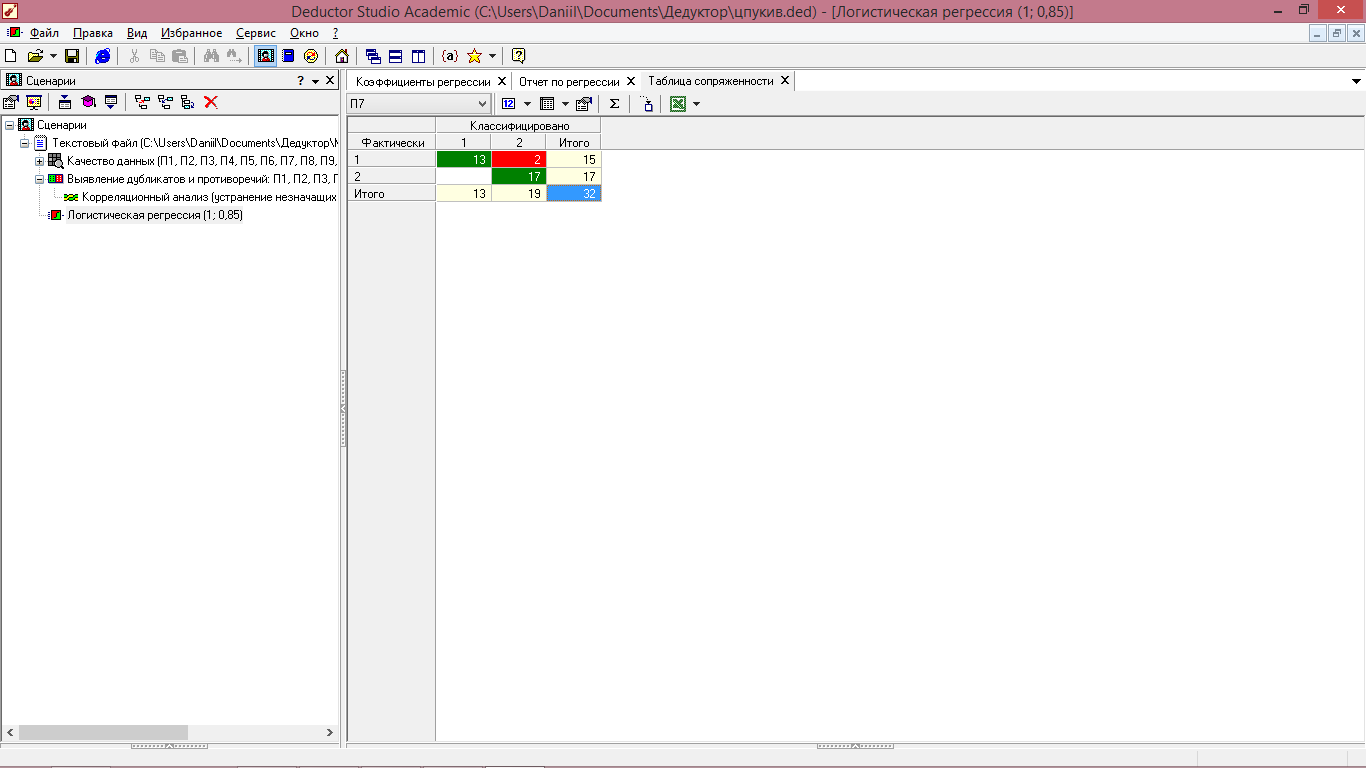
Рисунок 7.6 - Логистическая регрессия (таблица сопряженности в количестве примеров)
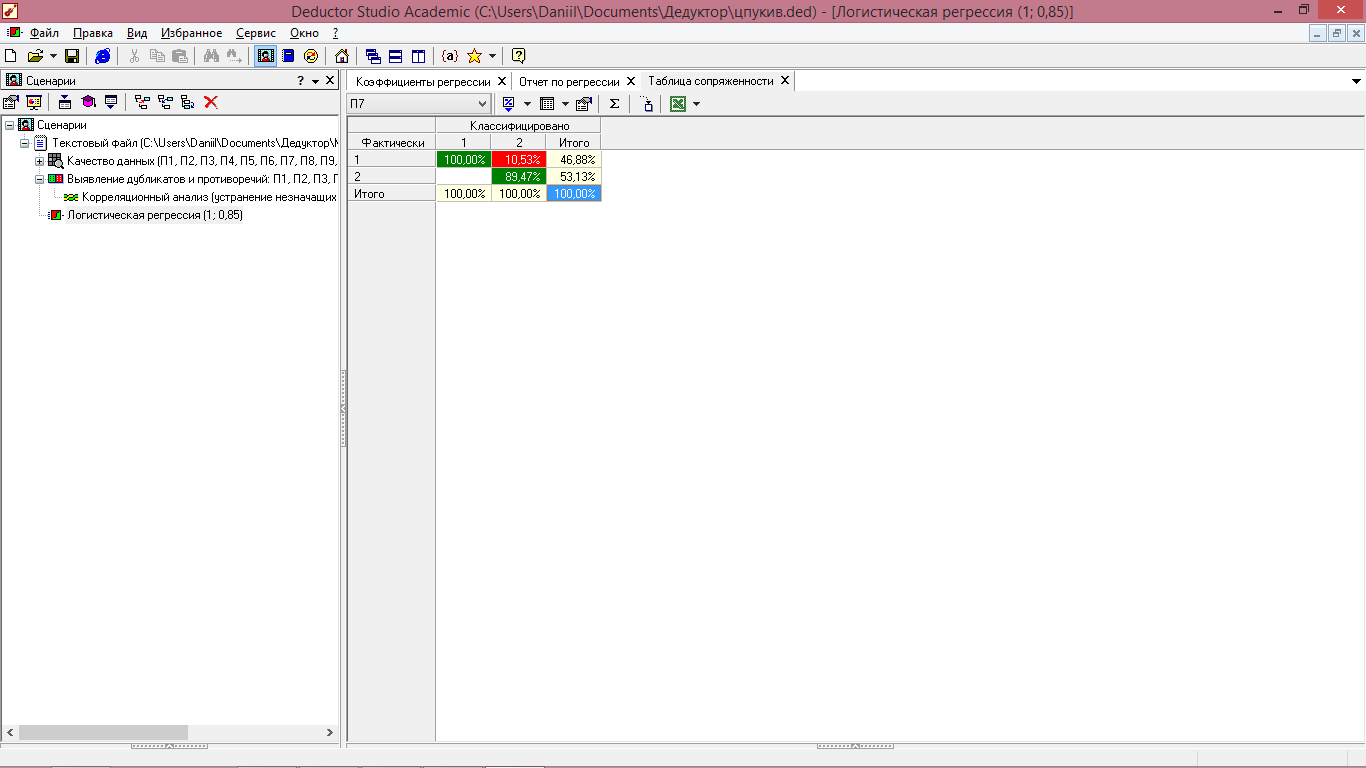
Рисунок 7.7- Логистическая регрессия (таблица сопряженности в процентном соотношении)
Качество классификации наглядно представлено ROC-кривой. ROC-кривая показывает зависимость количества верно классифицированных положительных примеров от количества неверно классифицированных отрицательных примеров. В терминологии ROC-анализа первые называются истинноположительным, вторые – ложноотрицательным множеством. При этом предполагается, что у классификатора имеется некоторый параметр, варьируя который, мы будем получать то или иное разбиение на два класса. Его часто называют порогом или точкой отсечения (cutoff value). В зависимости от него будут получаться различные величины ошибок I и II рода.
По рисунку видно: чувствительность, т.е. доля истинно положительных случаев равна 91,67%, специфичность, т.е. доля истинно отрицательных случаев равна 88,89%
Логистическая регрессия на выходе рассчитала значение рейтинга, которое можно трактовать как вероятность того, что событие наступит для конкретного испытуемого, т.е. что тип рабочего оборудования экскаватора будет прямая лопата.
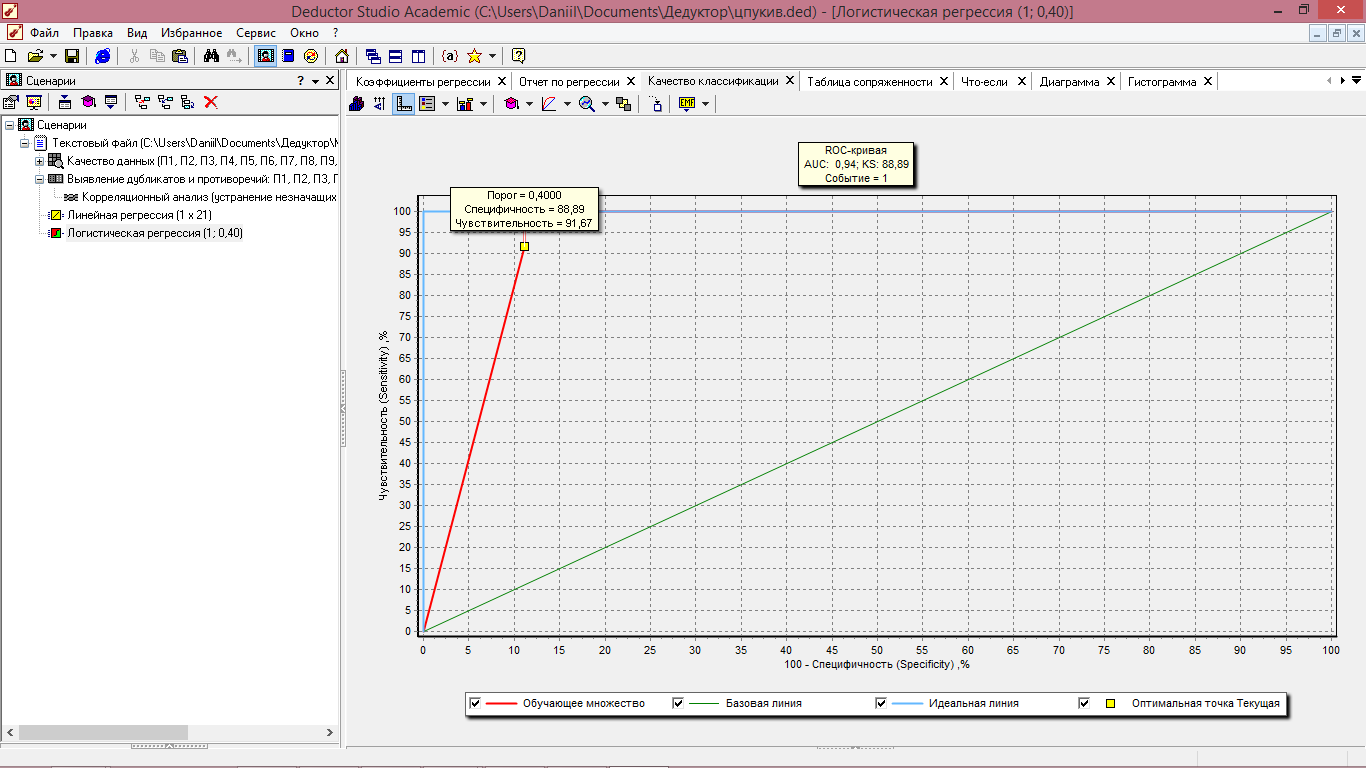
Рисунок 7.8 – ROC-кривая
8 Факторный анализ
Факторный анализ - процедура, с помощью которой большое число переменных, относящихся к имеющимся наблюдениям, сводится к меньшему количеству независимых влияющих величин, называемых факторами. При этом в один фактор объединяются переменные, сильно коррелирующие между собой. Переменные из разных факторов слабо коррелируют между собой. Таким образом, целью факторного анализа является нахождение таких комплексных факторов, которые можно более полно объединяют наблюдаемые связи между переменными имеющимися в наличии. [5]
Порядок выполнения факторного анализа в ПАП «DEDUCTOR» следующий:
1 Шаг - выбираем все возможные факторы для анализа фактора для анализа - все 14 входных параметров, рисунок 8.1.
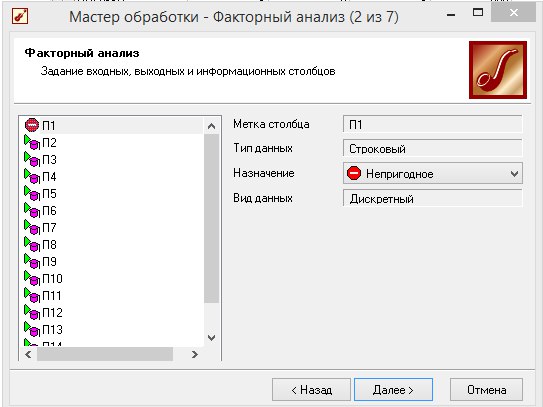
Рисунок 8.1 - Факторный анализ (задание входных и выходных параметров)
2 Шаг – задаем метод факторного решения и числа выделяемых факторов. Выбираем «метод ортогонального вращения – варимакс (с вращением по Кайзеру), при котором критерием является упрощение описания каждого фактора. В результате чего максимизируется нагрузка на каждый факто относительно небольшого числа переменных, а факторные нагрузки остальных нагрузок минимизируются. [3] Число выделяемых факторов – 3, нажимаем «Далее» (рисунок 8.2).
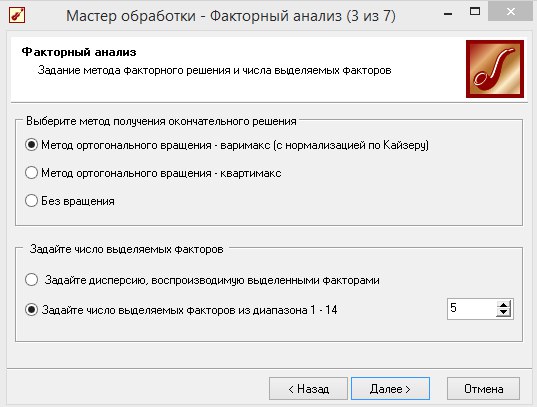
Рисунок 8.2 - Факторный анализ (задание метода факторного решения)
3 Шаг – запускаем вычисление исходных факторов методом главных компонент, нажимаем «Далее».
Метод главных компонент сводится к выбору новой ортогональной системы координат в пространстве наблюдений. В качестве главной компоненты избирают направление, вдоль которого массив данных имеет наибольший разброс, в выбор каждой последующей происходит так, чтобы разброс данных вдоль нее был максимальным и чтобы она была ортогональна другим главным компонентам, выбранным прежде. [6]
Происходит уточнение числа выделяемых факторов в соответствии с желаемой долей воспроизводимой ими дисперсии, устанавливаем порог значимости 88%, нажимаем «Далее» (рисунок 8.3).
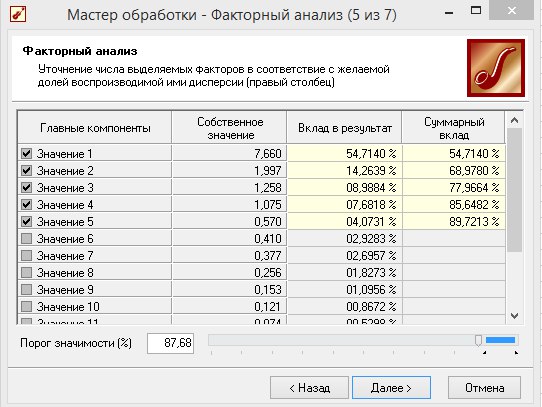
Рисунок 8.3 - Факторный анализ (уточнение числа выделяемых факторов)
4 Шаг – выбираем способ отображения данных как «Факторный анализ. Матрица факторного отображения», задаем имя и метку, нажимаем «Готово»
В открывшемся окне видим (рисунок 60), что платформа объединила девять факторов в значимый Фактор (рисунок 8.4).
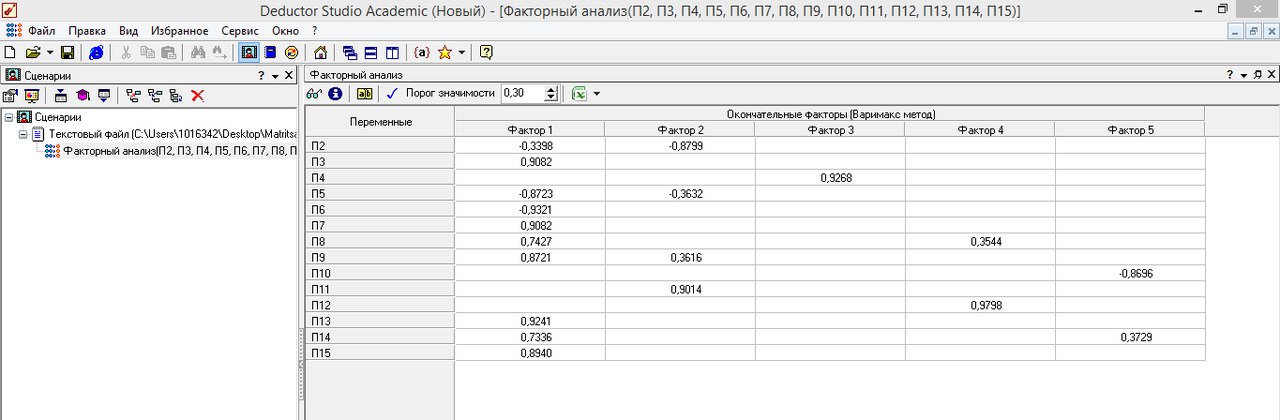
Рисунок 8.4 - Факторный анализ (выбор способа отображения данных)
В результате проведенного факторного анализа можем сделать вывод, что в один Фактор, который будет определять эксплуатационные показатели электроперфоратов в большей степени объединяются 9 входных факторов: тип питания перфоратора, тип крепления бура/сверла, максимальное число оборотов холостого хода, максимальная частота ударов, режим работы – сверление, максимальный диаметр сверления (полой коронкой), максимальная энергия удара, вес, цена, режим работы – шуруповерт.
Остальные факторы также можно объединить в другие, но они будут менее значимы.
Заключение
В рамках данной работы было необходимо провести обработку полученных экспериментальных данных.
Под «данными» понимаются фиксированные воспринимаемые факты окружающего мира. В работе в качестве данных были использованы результаты исследований 15-ти показателей 30-ти образцов электрических перфораторов, они были сведены в матрицу данных.
Информация используется при решения конкретных задач, когда известен метод преобразования данных. Можно сделать вывод, что информация существует только во время взаимодействия данных и метода, то есть, например, в данной работе, при применении метода логистической регрессии для установления вероятности наступления события (прохождения образцом масла испытания на прозрачность при 5°С) данные о испытаниях на прозрачность и содержании механических примесей в образце масла являлись информацией.
Знания – результаты решения задач, истинная информация, обобщенная в виде законов, теорий, совокупностей взглядов и представлений. Исходя из определения, можем сделать вывод, что каждый примененный метод позволил получить некоторые знания об этой совокупности образцов масла.
Например, корреляционный анализ позволил определить взаимосвязи между каждой парой показателей, которые в большинстве своем оказались слабыми (максимальное значение -0,370).
Регрессионный анализ позволил определить, что между показателя П5 и П12, которые имели самое высокое значение коэффициента корреляции, нет линейной связи и связи более высокого порядка.
Логистическая регрессия позволила определить вероятность наступления события (прохождения образцами трансформаторного масла испытания на прозрачность) в зависимости от наличия/отсутствия в образцах масла механических примесей. Было установлено, что в 100% случаев образец масла проходил испытание на прозрачность, если в нем не содержались механические примеси и наоборот.
Факторный анализ позволил определить степень совместного влияния таких показателей как тангенс угла диэлектрических потерь и плотность при 20°С, на трансформаторное масло.
Все эти методы позволили установить новые связи и закономерности, существующие в полученной экспериментальным путем базе данных.
Список использованных источников
1 Интернет площадка, объединяющая цены и характеристики продуктов из разных магазинов, Яндекс-маркет – Режим доступа https://market.yandex.ru/articles/kak-vybrat-perforator?track=fr_ctlg_list
2 Теория функций комплексной переменной: учебно-методическое пособие / М.Ю. Васильчик, Г.Б. Корабельникова, Т.М. Назарова, Л.В. Роева, Р.И. Святкина, И.В. Синенко. - Новосиб. гос. техн. ун-т, 2003. - 56 c.
3 Справка ПАП «DEDUCTOR»
4 Электронный ресурс: https://basegroup.ru/
5 Бююль А. SPSS: искусство обработки информации. Анализ статистических данных и восстановление скрытых закономерностей / А. Бююль, П. Цёфель. – Москва::DiaSoft, 2002. – 605 с.
6 Дорогонько, Е.В. Обрабтка и анализ социологически данных с помощью пакета SPSS: учебно-методическое пособие / Е.В. Дорогонько. – Сургут: Издательский центр СрГУ, 2010. – 60 с.