Линейный одномерный регрессионный анализ
В целях исследований часто бывает удобно представить исследуемый объект в виде ящика, имеющего входы и выходы, не рассматривая детально его внутренней структуры. Конечно, преобразования в ящике (на объекте) происходят (сигналы проходят по связям и элементам, меняют свою форму и т. п.), но при таком представлении они происходят скрыто от наблюдателя.
Значения на входах и выходах черного ящика можно наблюдать и измерять. Содержимое ящика неизвестно.
Задача состоит в том, чтобы, зная множество значений на входах и выходах, построить модель, то есть определить функцию ящика, по которой вход преобразуется в выход. Такая задача называется задачей регрессионного анализа.
Проведем регрессионный анализ для двух переменных, которые имеют самую большую зависимость из всех исследуемых (определили посредством корреляционного анализа). Это П5 – Максимальное число оборотов холостого хода и П6– максимальная частота ударов.
Ставим задачу: Как максимальная частота ударов от максимального числа оборотов холостого хода П6(П5)?
Для начала предположим, что мы имеем дело с черным ящиком, имеющим один вход и один выход. Допустим для простоты, что зависимость между входом и выходом линейная или почти линейная. Тогда данная модель будет называться линейной одномерной регрессионной моделью. То есть выход Y зависит от входа X линейно, то есть гипотеза имеет вид:
Y = A1X + A0+S
Одномерная линейная модель представлена на рисунке
Рисунок 6.1 – Одномерная линейная модель
Результаты, полученные при корреляционном анализе, используем для построения линейных регрессионных моделей.
1 Шаг - на панели «Сценарии» выбираем соответствующий обработчик.
2 Шаг – в открывшемся окне для показателя П5 устанавливаем, как «Входное», для показателя П6 «Выходное», нажимаем «Далее»
3 Шаг – производим разбиение исходного набора данных на подмножества, нажимаем «Далее» (рисунок 6.1).
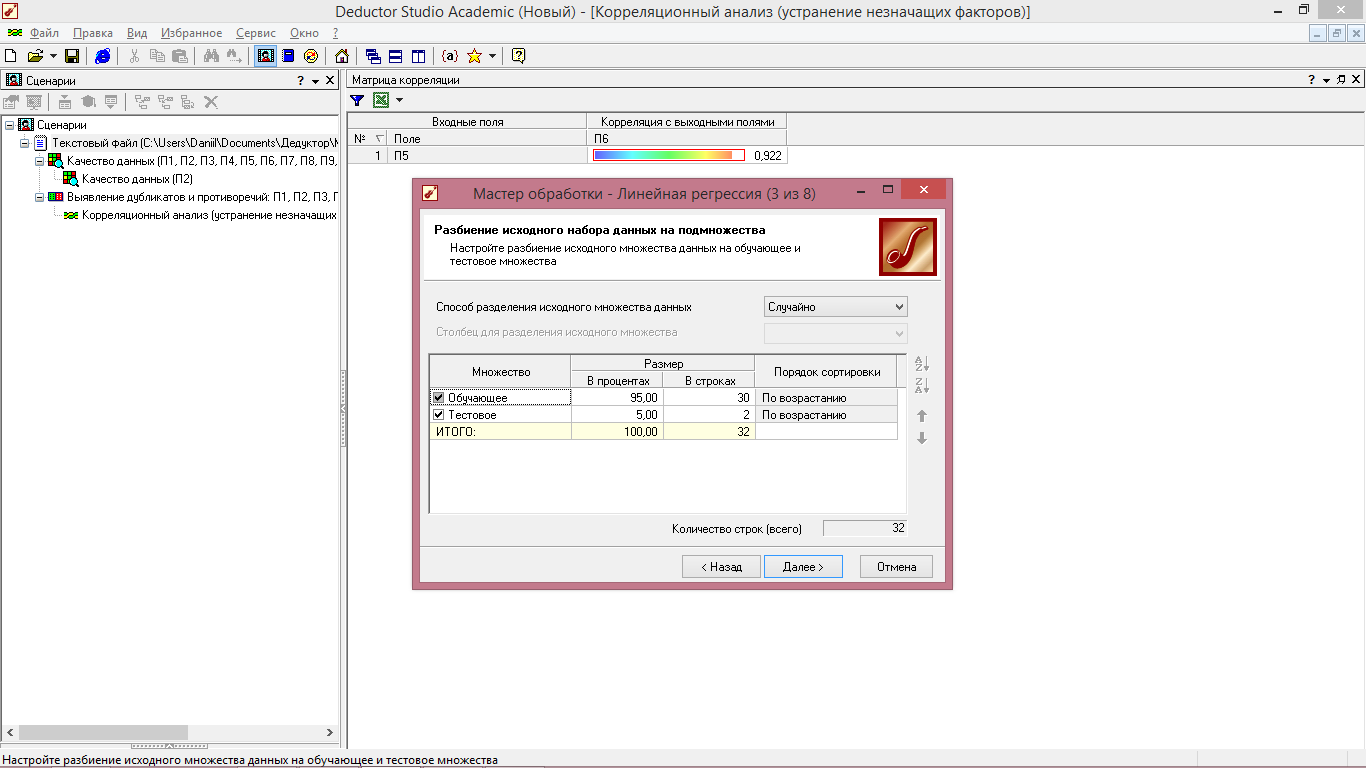
Рисунок 6.2 - Линейная регрессия (разбиение исходного набора данных на подмножества)
4 Шаг – при необходимости производим настройку диапазона выходных значений, нажимаем «Далее» (рисунок 6.2).
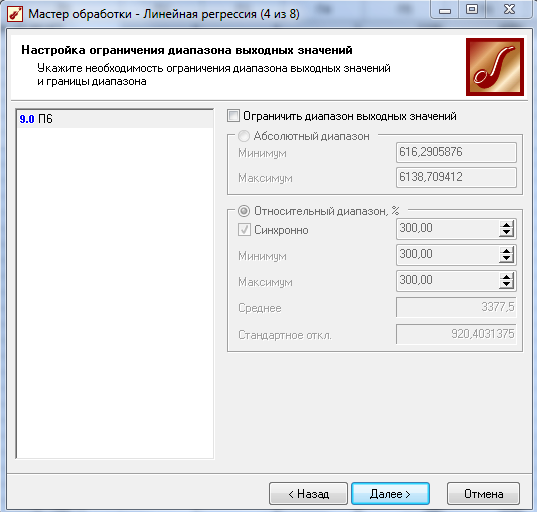
Рисунок 6.3 - Линейная регрессия (настройка диапазона выходных значений)
5 Шаг – производим настройку отбора переменных в регрессионную модель, для этого выбираем «Полное включение (Enter)», нажимаем «далее» (рисунок 6.3).
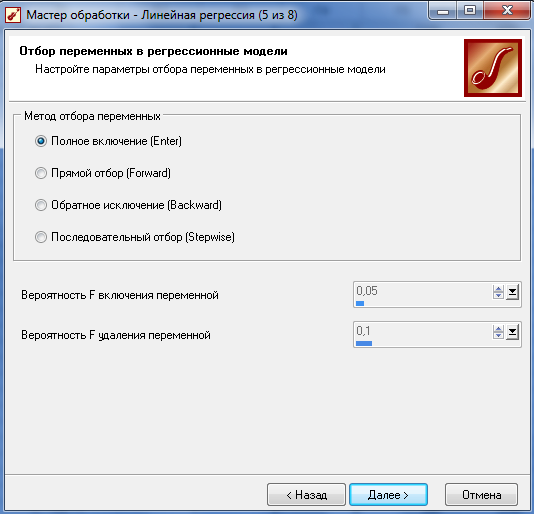
Рисунок 6.4 - Линейная регрессия
(настройка параметров отбора переменных в регрессионную модель)
6 Шаг – запускаем процесс построения линейной модели, нажимаем «Пуск» и ждем, пока в графе «Название процесса» не отобразится «Успешное завершение», а в графе «Процент выполнения текущего процесса» - 100%, после чего нажимаем «Далее».
7 Шаг – способы отображения данных «Коэффициенты регрессии», «Отчет по регрессии», «Диаграмма рассеяния), назначаем имя и метку, нажимаем «Готово».
Полученные коэффициенты регрессии отражены на рисунке 6.4 и в формуле (3), но нужно помнить, что значение коэффициента корреляции не близко к 1, следовательно, гипотеза о линейности не подтвердилась.
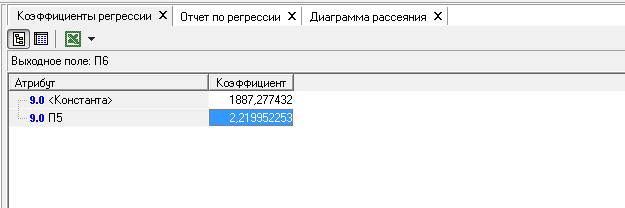
Рисунок 6.5 - Коэффициенты линейной регрессии
Вкладка «Отчет по регрессии» (рисунок 6.5) позволяет увидеть значение коэффициента детерминации, равного 0,9843. Это говорит о том, что качество регрессионной модели является высоким.
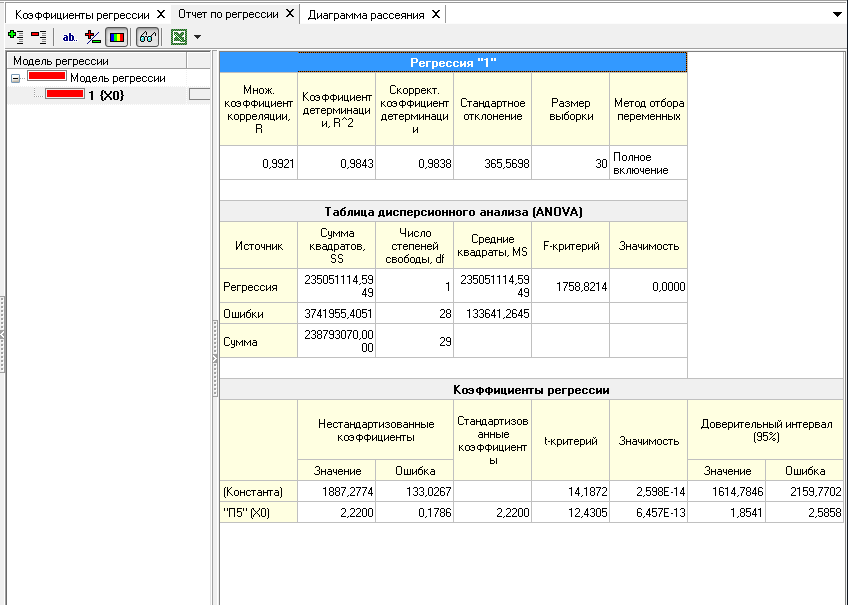
Рисунок 6.6 - Отчет по линейной регрессии
Формула регрессии отражена в формуле (3):
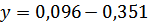Y = 2.22X-1887.3(3)
Вкладка «Диаграмма рассеяния» позволяет графически увидеть распределение данных согласно регрессионной модели (рисунок 6.6). Прямая диагональная синяя линия представляет собой ориентир (линию идеальных значений). Чем ближе точка к этой линии, тем меньше ошибка модели. Также на диаграмме рассеяния отображаются две пунктирные линии – верхняя и нижняя границы доверительного интервала. Его ширина определяется допустимой ошибкой, которая вводится в поле «Ошибка». Если она (величина в столбце <Имя_поля>_ERR) меньше допустимой, то точка попадает в доверительный интервал. [3]
Средняя часть расчётов отражает два источника дисперсии: дисперсию, которая описывается уравнением регрессии (сумма квадратов, обусловленная регрессией) и дисперсию, которая не учитывается при записи уравнения (остаточная сумма квадратов). Частное от суммы квадратов, обусловленных регрессией и остаточной суммы квадратов называется "коэффициентом детерминации". В таблице результатов это частное выводится под именем "R2". В нашем примере мера определённости равна:
235051114,59/238793070=0,9843
То есть построенная регрессия объясняет 98.43% разброса значения переменной Y относительно среднего.
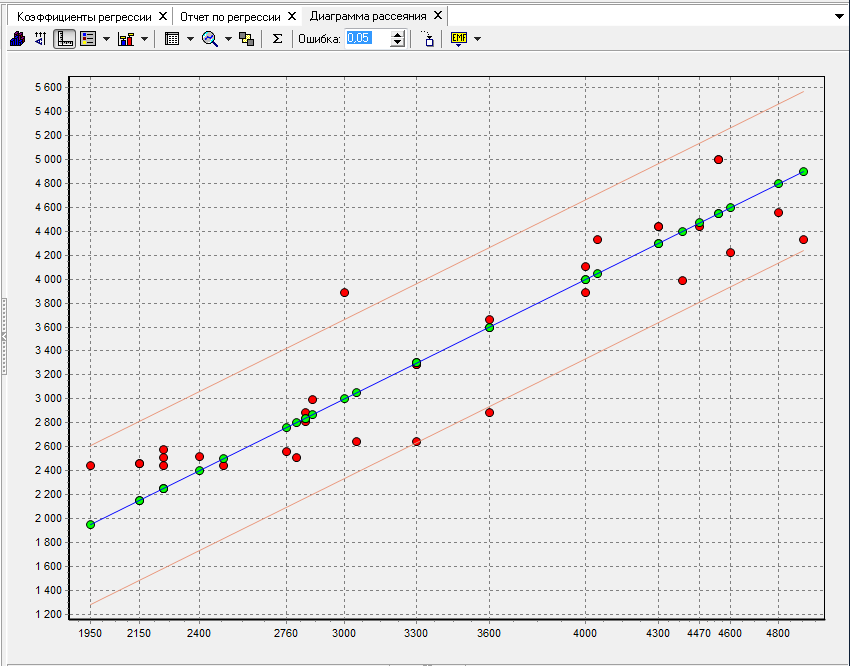Рисунок 6.7 - Диаграмма рассеяния линейной регрессии
Коэффициент детерминации измеряет долю разброса относительно среднего значения, которую «объясняет» построенная регрессия. Коэффициент детерминации лежит в пределах от 0 до 1. Он измеряет качество построенной регрессии. Чем ближе коэффициент детерминации к 1, тем лучше регрессия «объясняет» зависимость в данных. Значение коэффициента детерминации возрастает с ростом числа переменных в регрессии, что не означает улучшения качества предсказания.
Как видно из рисунка в поле, ограниченной линиями Y+S и YS не попадает 1 точка, что составляет 3,33% всех значений, соответственно попадают в эту область 96,66% (порог 95%), что говорит о том, что выдвинутая нами гипотеза о том, что зависимость максимальной частоты ударов от максимального числа оборотов холостого хода – верная.
6.2 Линейный многомерный регрессионный анализ
Предположим, что функциональная структура ящика снова имеет линейную зависимость, но количество входных сигналов, действующих одновременно на объект, равно m:
Y = A0 + A1 · X1 + … + Am · Xm.+ S
В таком случае модель черного ящика будет выглядеть следующим образом:
Рисунок6.8 – Модель черного ящика линейного многомерного регрессионного анализа
Построим линейную двумерную регрессионную модель зависимости .
Работаем также в Мастере обработки Линейная регрессия.
1 шаг. В качестве входных параметров выберем П5 и П11 , в качестве выходного П6, остальные отметим как неиспользуемые.
2 шаг. В качестве способа отображения выбираем диаграмму рассеяния, коэффициенты регрессии и отчет по регрессии. Рассмотрим визуализатор отчет по регрессии. Здесь видим коэффициент регрессии А1 = 2,1962, А2 = 0,5828 и смещение по оси ординат А0 под именем "константа" =1648,51. То есть, уравнение регрессии выглядит следующим образом:
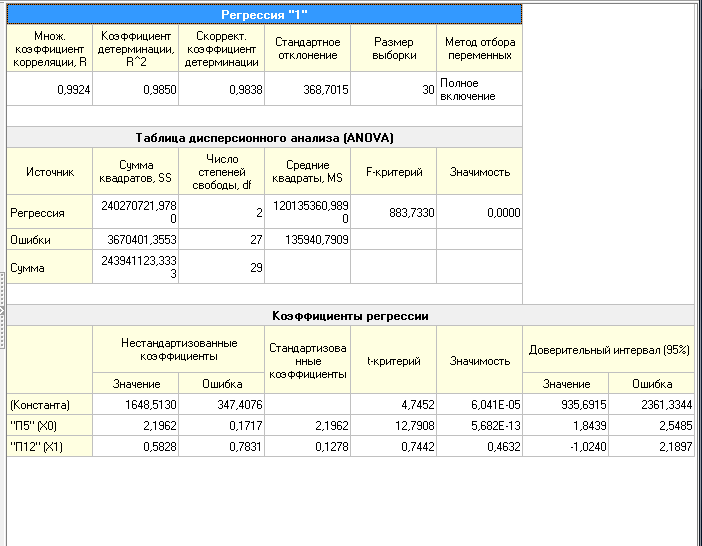
Рисунок 6.9 – Отчет по многомерной линейной регрессии
Y = 2,1962 • X1+,5828• X2+1648,51
Коэффициент детерминации равен 0,985
То есть построенная регрессия объясняет 98,5% разброса значения переменной Y относительно среднего.
. 
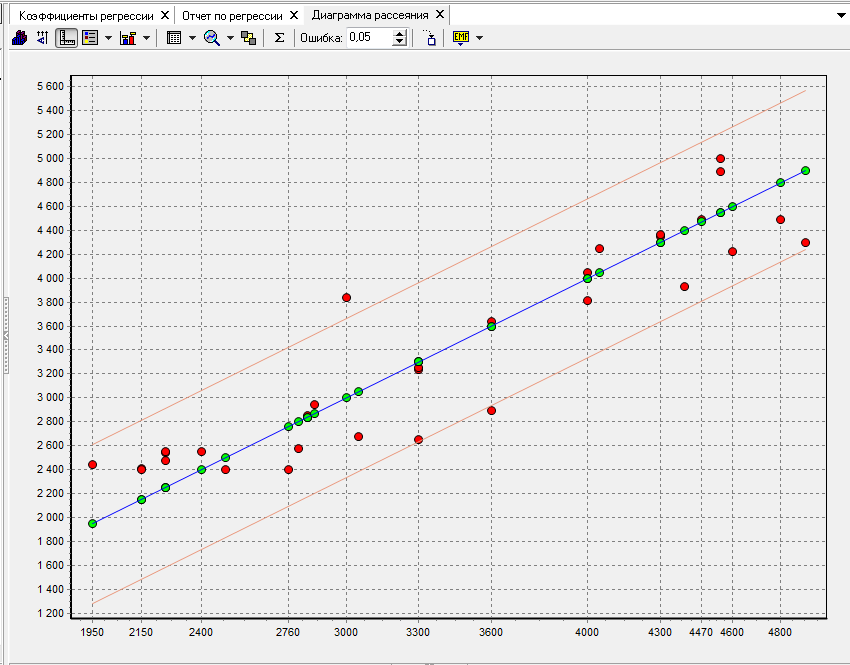
Рисунок 6.10 Диаграмма рассеяния
Как видно из рисунка в поле, ограниченной линиями Y+S и YS не попадает 1 точка, что составляет 3% всех значений, соответственно попадают в эту область 97% (порог 68,27%), что говорит о том, что выдвинутая нами гипотеза о том, что зависимость максимальной частоты ударов П6 от максимального числа оборотов холостого хода П5 и длины перфоратора П11– верная.
Построим линейную трехмерную регрессионную модель зависимости максимальной частоты ударов П6 от максимального числа оборотов холостого хода П5, длины сетевого кабеля П11 и длины перфоратора П12.
Работаем также в Мастере обработки Линейная регрессия. На первом шаге в качестве входных параметров выберем П5, П11 и П12, в качестве выходного П6, остальные отметим как неиспользуемые.
В качестве способа отображения выбираем диаграмму рассеяния, коэффициенты регрессии и отчет по регрессии.
Рассмотрим визуализатор отчет по регрессии: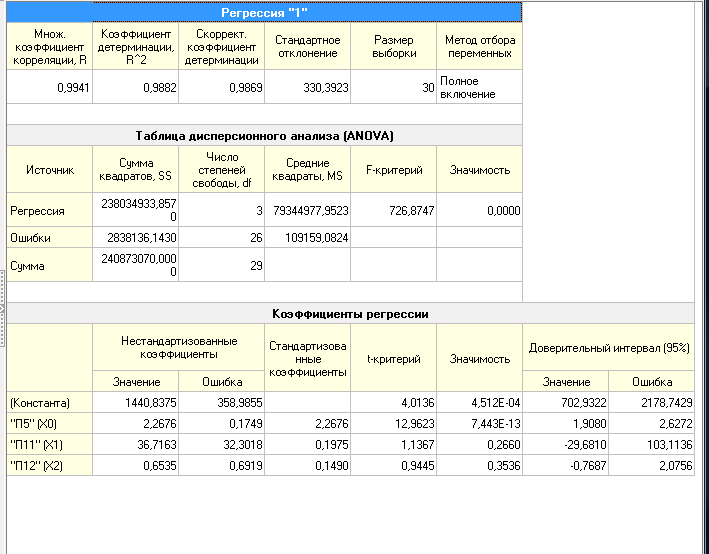 
Рисунок 6.11 – Отчет по регрессии
Здесь видим коэффициент регрессии А1 = 2,27, А2 = 36,72, А3 = 0,66 и смещение по оси ординат А0 под именем "константа" = 1440,8. То есть, уравнение регрессии выглядит следующим образом:
Y = 2,27 • X1+36,72• X2+0,66• X2 +1440,8
Коэффициент детерминации равен 0,9882
То есть построенная регрессия объясняет 98,82% разброса значения переменной Y относительно среднего.
На рисунке 6.12 представлена диаграмма рассеяния: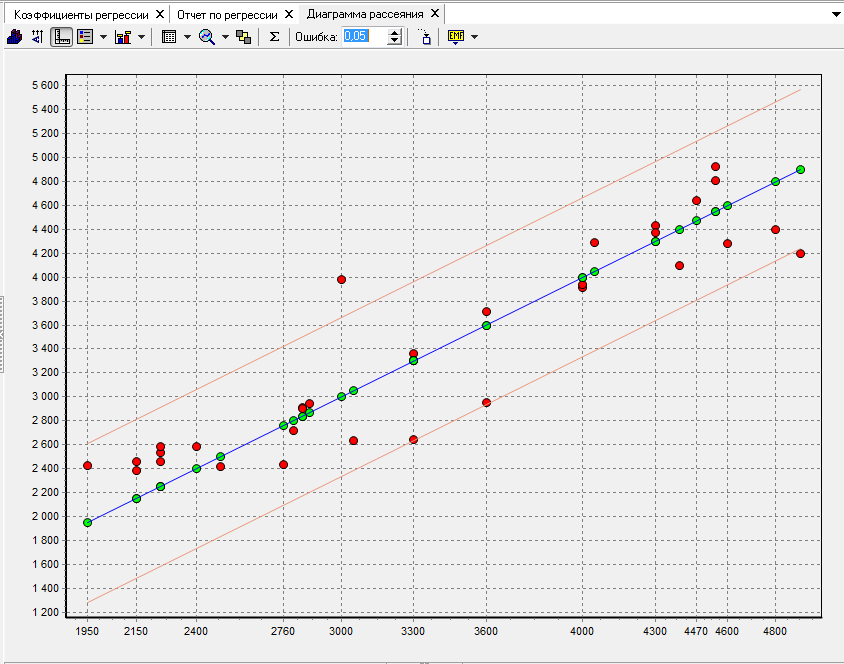 
Рисунок 6.12 – Диаграмма рассеяния
Как видно из рисунка в поле, ограниченной линиями Y+S и YS не попадает 2 точки, что составляет 6,67% всех значений, соответственно попадают в эту область 93% (порог 68,27%), что говорит о том, что выдвинутая нами гипотеза о том, что зависимость максимальной частоты ударов П6 от максимального числа оборотов холостого хода П5, длины сетевого кабеля П11 и длины перфоратора П12 имеет линейную зависимость – верная.
6.3 Нелинейная регрессия
В общем случае в регрессионный анализ вовлекаются несколько независимых переменных и необходимо оценить коэффициенты уравнения.
Переменные, объявленные независимыми, могут сами коррелировать между собой; этот факт необходимо обязательно учитывать при определении коэффициентов уравнения регрессии для того, чтобы избежать ложных корреляций.
При работе с множественной регрессией, в отличие от парной, необходимо определять алгоритм анализа. Стандартный алгоритм включает в итоговую регрессионную модель все имеющие предикторы. Пошаговый алгоритм предполагает последовательное включение (исключение) независимых переменных, исходя, из объяснительного «веса». Пошаговый метод хорош, когда имеется много независимых переменных; он «очищает» модель от откровенно слабых предикторов, делая ее более компактной и лаконичной.
Дополнительным условием корректности множественной регрессии (наряду с интервальностью, нормальностью, линейностью) является отсутствие мультиколлинеарности – наличия сильных корреляционных связей между независимыми переменными. [6]