6 Моделирование и анализ зависимостей между количественными признаками

Дата: 2025-05-25; Просмотры: 4

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Если расчёт корреляции характеризует силу связи между двумя переменными, то регрессионный анализ служит для определения вида этой связи и дает возможность для прогнозирования значения одной (зависимой) переменной отталкиваясь от значения другой (независимой) переменной.

Для проведения линейного регрессионного анализа зависимая переменная должна иметь порядковую шкалу. В то же время, бинарная логистическая регрессия выявляет зависимость дихотомической переменной от некой другой переменной, относящейся к любой шкале. Те же условия применения справедливы и для пробит-анализа. Если зависимая переменная является категориальной, но имеет более двух категорий, то здесь подходящим методом будет мультиномальная логистическая регрессия. И, наконец, можно анализировать и нелинейные связи между переменными, которые относятся к интервальной шкале. Для этого предназначен метод нелинейной регрессии.

Простая линейная регрессия:

Этот вид регрессии лучше всего подходит для того, чтобы продемонстрировать основополагающие принципы регрессионного анализа. В таком случае говорят о линейной связи:

,

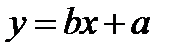где b — регрессионные коэффициенты, a — смещение по оси ординат.

Смещение по оси ординат соответствует точке на оси у (вертикальной оси), где прямая регрессии пересекает эту ось. Коэффициент регрессии b через соотношение

b=tg(a),

указывает на угол наклона прямой.

При проведении простой линейной регрессии основной задачей является определение параметров b и а. Оптимальным решением этой задачи является такая прямая, для которой сумма квадратов вертикальных расстояний до отдельных точек данных является минимальной.

Множественная линейная регрессия:

В общем случае в регрессионный анализ вовлекаются несколько независимых переменных. Это, конечно же, наносит ущерб наглядности получаемых результатов, так как подобные множественные связи, в конце концов, становится невозможно представить графически.

В случае множественного регрессионного анализа речь идѐт необходимо оценить коэффициенты уравнения

y = b ₁ - x ₁ + b ₂ - x ₂ +….+ b_n - x_n + a,

Регрессионный анализ используется для нахождения уравнения, которое связывает зависимую переменную (отклик) с одной или несколькими независимыми переменными (предикторами).

Суть регрессионного анализа заключается в нахождении наиболее важных факторов, которые влияю на зависимую переменную.

где n — количество независимых переменных, обозначенных как х1 и хn, — некоторая константа.

Переменные, объявленные независимыми, могут сами коррелировать между собой; этот факт необходимо обязательно учитывать при определении коэффициентов уравнения регрессии для того, чтобы избежать ложных корреляций.

Для множественного анализа с несколькими независимыми переменными не рекомендуется оставлять метод включения всех переменных, установленный по умолчанию. Этот метод соответствует одновременной обработке всех независимых переменных, выбранных для анализа, и поэтому он может рекомендоваться для использования только в случае простого анализа с одной независимой переменной. Для множественного анализа следует выбрать один из пошаговых методов. При прямом методе независимые переменные, которые имеют наибольшие коэффициенты частичной корреляции с зависимой переменной, пошагово увязываются в регрессионное уравнение. При обратном методе начинают с результата, содержащего все независимые переменные, и затем исключают независимые переменные с наименьшими частичными корреляционными коэффициентами, пока соответствующий регрессионный коэффициент не оказывается незначимым.

Наиболее распространенным является пошаговый метод, который устроен так же, как и прямой метод, однако после каждого шага переменные, используемые в данный момент, исследуются по обратному методу. При пошаговом методе могут задаваться блоки независимых переменных; в этом случае заданные блоки на одном шаге обрабатываются совместно.

Нелинейная регрессия:

Многие связи по своей природе, то есть в реальной жизни, либо являются строго линейными, либо их можно привести к линейному виду.

Бинарная логистическая регрессия:

С помощью метода бинарной логистической регрессии можно исследовать зависимость дихотомических переменных от независимых переменных, имеющих любой вид шкалы.

Как правило, в случае с дихотомическими переменными речь идѐт о некотором событии, которое может произойти или не произойти; бинарная логистическая регрессия в таком случае рассчитывает вероятность наступления события в зависимости от значений независимых переменных.

Вероятность наступления события для некоторого случая рассчитывается по формуле

,

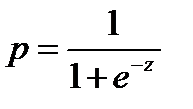где 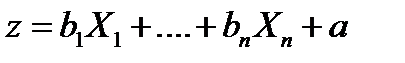, X ₁— значения независимых переменных, b1 — коэффициенты, расчёт которых является задачей бинарной логистической регрессии, a— некоторая константа.

Если для p получится значение меньшее 0,5, то можно предположить, что событие не наступит; в противном случае предполагается наступление события.

Мультиномиальная логистическая регрессия:

Этот метод является вариантом логистической регрессии, при которой зависимая переменная не является дихотомической, как при бинарной логистической регрессии, а имеет больше двух категорий. В то время как, при бинарной логистической регрессии не-зависимая переменная может иметь интервальную шкалу, то мультиномиальная логисти-ческая регрессия пригодна только для категориальных независимых переменных, причѐм имеет значение, относятся ли они к шкале наименований или к порядковой шкале. Конеч-но же, не исключается возможность задания в качестве ковариат переменных, имеющих интервальную шкалу.

Порядковая регрессия:

Порядковая регрессия предназначена для целевой переменной, принадлежащей к порядковой шкале. Независимые переменные и здесь должны быть категориальными (то есть иметь номинальную или порядковую шкалу), однако в качестве ковариат допускается применение порядковой регрессии.

Коэффициент детерминации R² – показатель, насколько качественными являются данные, изменяется от 0 до 1 и чем ближе к 1, тем лучше регрессионная модель.

В общем виде регрессионная модель имеет вид уравнения (2):

Y = a₀ + X₁*a₁ + X₂*a₂ +...+ X_n*a_n + ɛ (2)

где Y – зависимая переменная (отклик);

X ₁ , X ₂ ,… X_n – независимые переменные (регрессоры);

ɛ - ошибка, учитывающая суммарное влияние факторов на модель;

а₀, а₁,…а _n - коэффициенты модели (параметры);

Таким образом, задача сводится к подбору коэффициентов a_i. Он производится методом наименьших квадратом (МНК). [6]

6.1 Линейная регрессия

Для проведения линейного регрессионного анализа зависимая переменная должна иметь порядковую шкалу. В то же время, бинарная логистическая регрессия выявляет зависимость дихотомической переменной от некой другой переменной, относящейся к любой шкале. Те же условия применения справедливы и для пробитанализа. Если зависимая переменная является категориальной, но имеет более двух категорий, то здесь подходящим методом будет мультиномиальная логистическая регрессия. И, наконец, можно анализировать и нелинейные связи между переменными, которые относятся к интервальной шкале. Для этого предназначен метод нелинейной регрессии.