5 Первичный анализ данных
5.1 Частотный анализ данных
5.1.1 Теоретические сведения
Анализ частотных распределений результатов исследования – это первый шаг при обработке информации. Первый шаг одномерного описательного анализа для объяснения какого-либо явления – его описание. Результаты любого исследования содержат множество данных и просто просмотр базы данных не дает возможности осмыслить такой массив информации.
В этом случае методы одномерного описательного анализа решают задачу сжатия исходной информации, ее компактного представления. Как правило, в процессе исследования бывает важно получить совокупные характеристики отдельных предметов через призму какого-либо конкретного свойства. Вместо большого числа отдельных показателей нам требуется одно значение, которое было бы типичным (репрезентативным) для всей совокупности объектов. Анализ одномерных распределений позволяет заодно установить, насколько типичное значение в действительности типично, репрезентативно по отношению к совокупности данных. [5]
5.1.2 Частотные таблицы
1 Шаг – для того, чтобы открыть частотные таблицы, необходимо открыть вкладку «Статистика» (рисунок 3.9), выбрать необходимый показатель и на панели нажать «Обзор статистики». В конкретном случае откроем частотную таблицу для показателя П5 (рисунок 5.1).
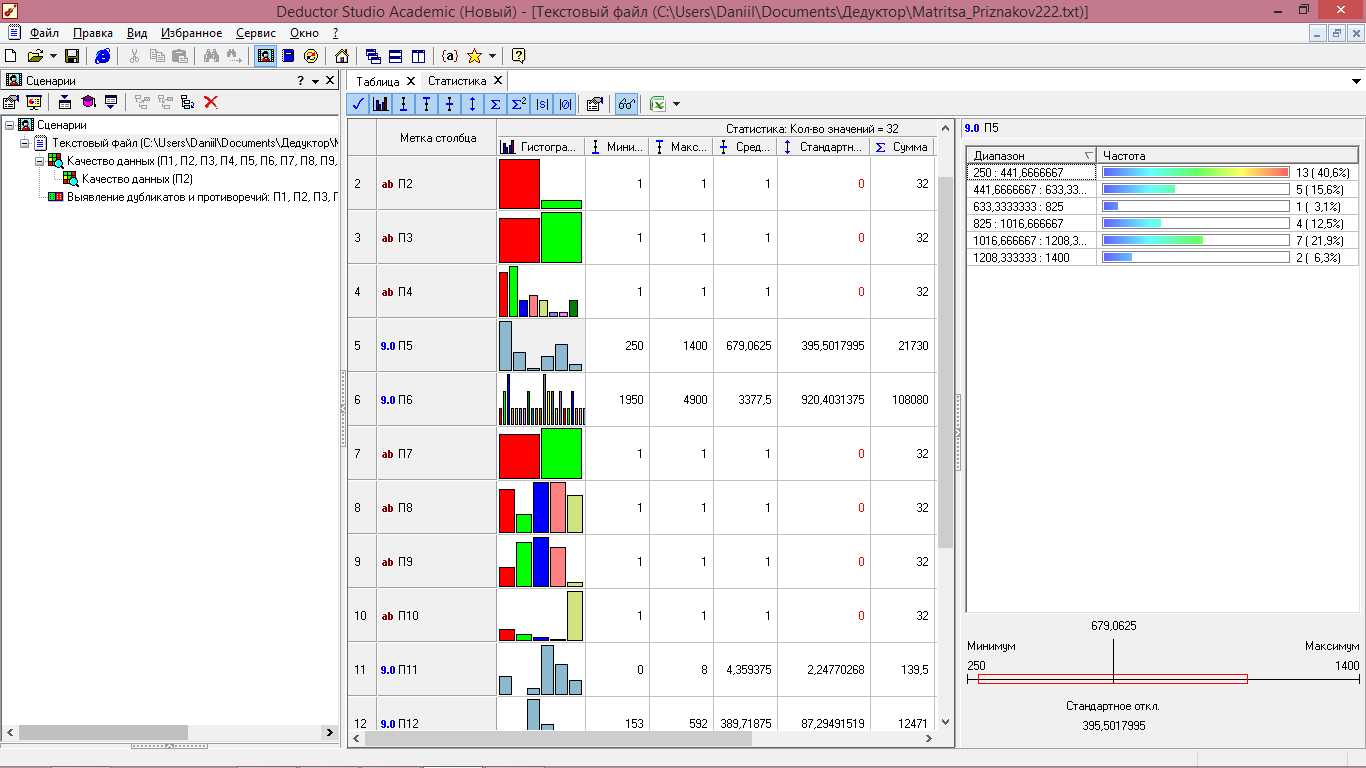
Рисунок 5.1 - Частотный анализ показателя П5 (максимальное число оборотов холостого хода)
В правой части откроется окно, содержащее информацию о частотном распределении. В верхней части все данные сгруппированы в 6 диапазонов и указано количество примеров (в том числе в процентном соотношении), входящих в данный диапазон. Для показателя П5 все данные сгруппировались в 3 основных диапазона:
- в диапазон, где максимальное число оборотов холостого хода составляет от 250 до 442, попали 13 образцов перфораторов (40,6% от общего количества);
- в диапазон, где максимальное число оборотов холостого хода составляет от 442 до 633 попали 5 образцов перфораторов (15,6% от общего количества);
- в диапазон, где максимальное число оборотов холостого хода составляет от 663 до 825, попали 1 образец перфораторов (3,1% от общего количества).
- в диапазон, где максимальное число оборотов холостого хода составляет от 825 до 1017, попали 4 образца перфораторов (12,5% от общего количества);
- в диапазон, где максимальное число оборотов холостого хода составляет от 1017 до 1208, попали 7 образцов перфораторов (21,9% от общего количества);
- в диапазон, где максимальное число оборотов холостого хода составляет от 1208 до 1400, попали 2 образца перфораторов (6,3% от общего количества).
В нижней части данного окна отражены максимальное 250 и минимальное 1400 значения, а также стандартное отклонение данных показателя 395,5.
Также распределение данных по диапазонам можно отразить в графическом виде с помощью гистограммы. Для этого необходимо при выборе способа отображения (рисунок 5.2) поставить флажок напротив «Гистограмма» и выбрать нужный показатель.
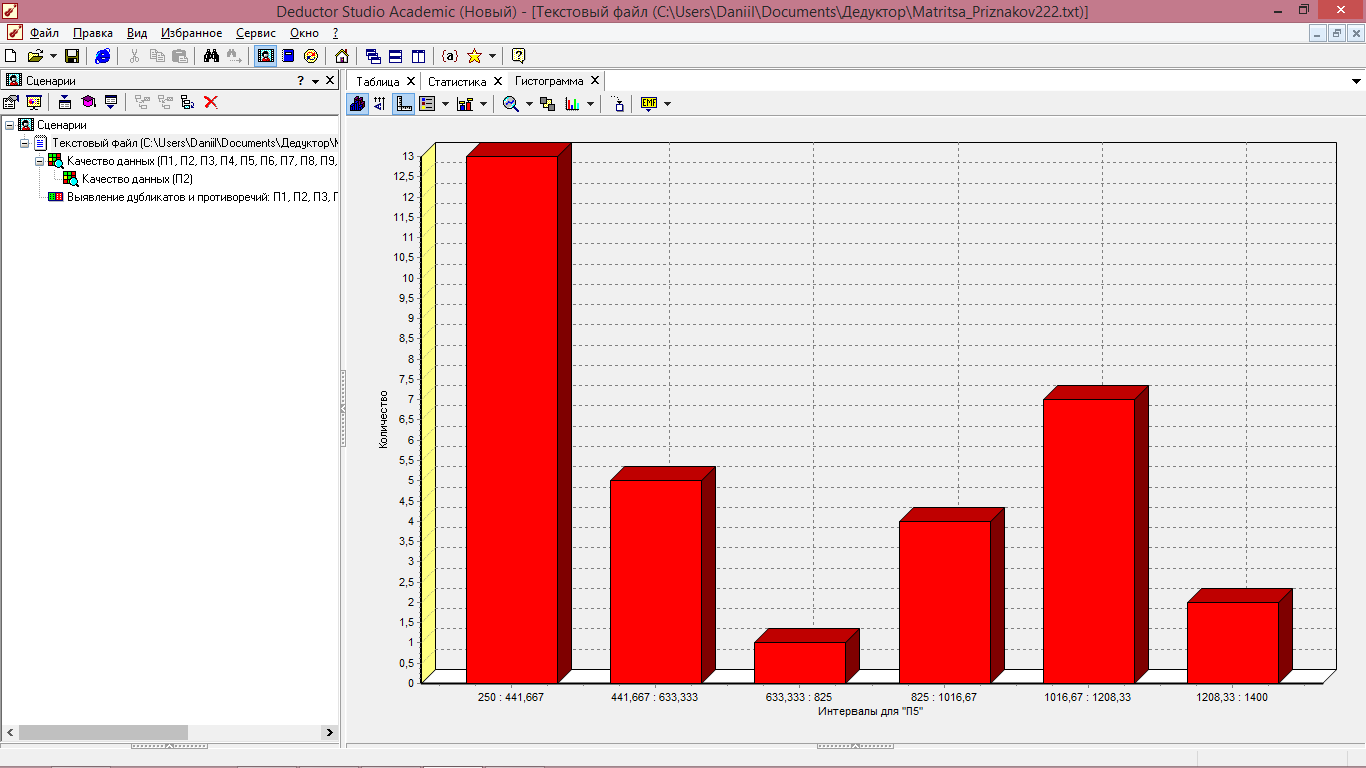
Рисунок 5.2 - Гистограмма распределения показателя П5 (максимальное число оборотов холостого хода)
Далее будут приведена частотная таблица и гистограмма для второго количественного показателя П6 (максимальное число ударов).
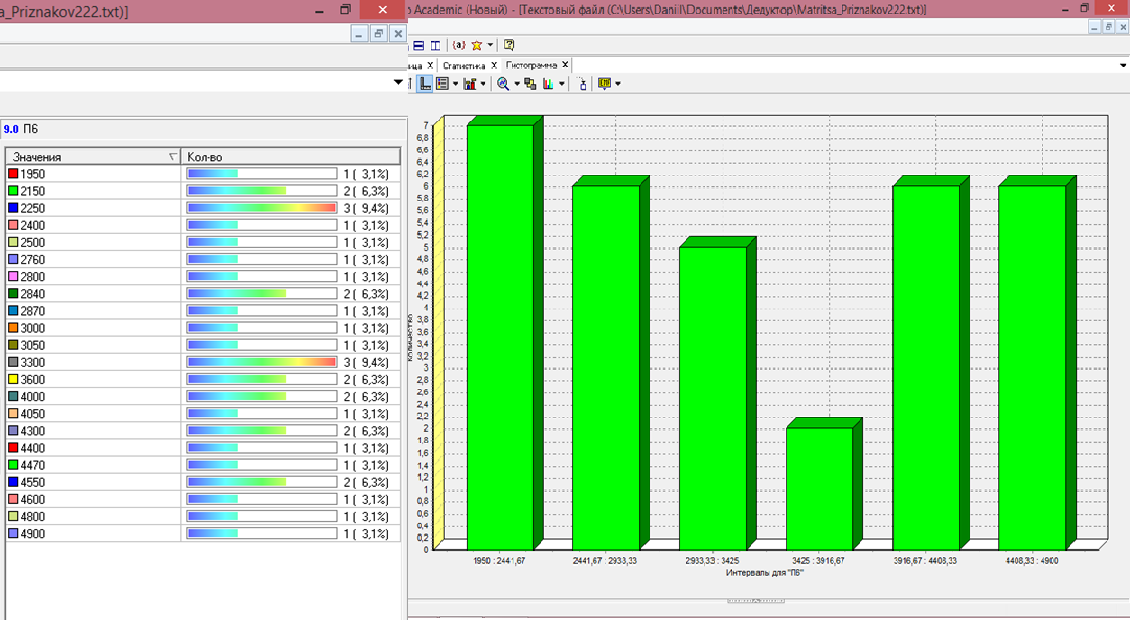
а) б)
Рисунок 5.3 - Частотная таблица (а) и гистограмма (б) для количественного показателя П2
(максимальное число ударов)
Построение гистограмм в ПАП «DEDUCTOR» возможно только для количественных показателей, поэтому для показателей номинальной шкалы П4 (фирма производитель) и П9 (Максимальный диаметр сверления полой коронкой) были построены частотные таблицы (рисунок 5.4).
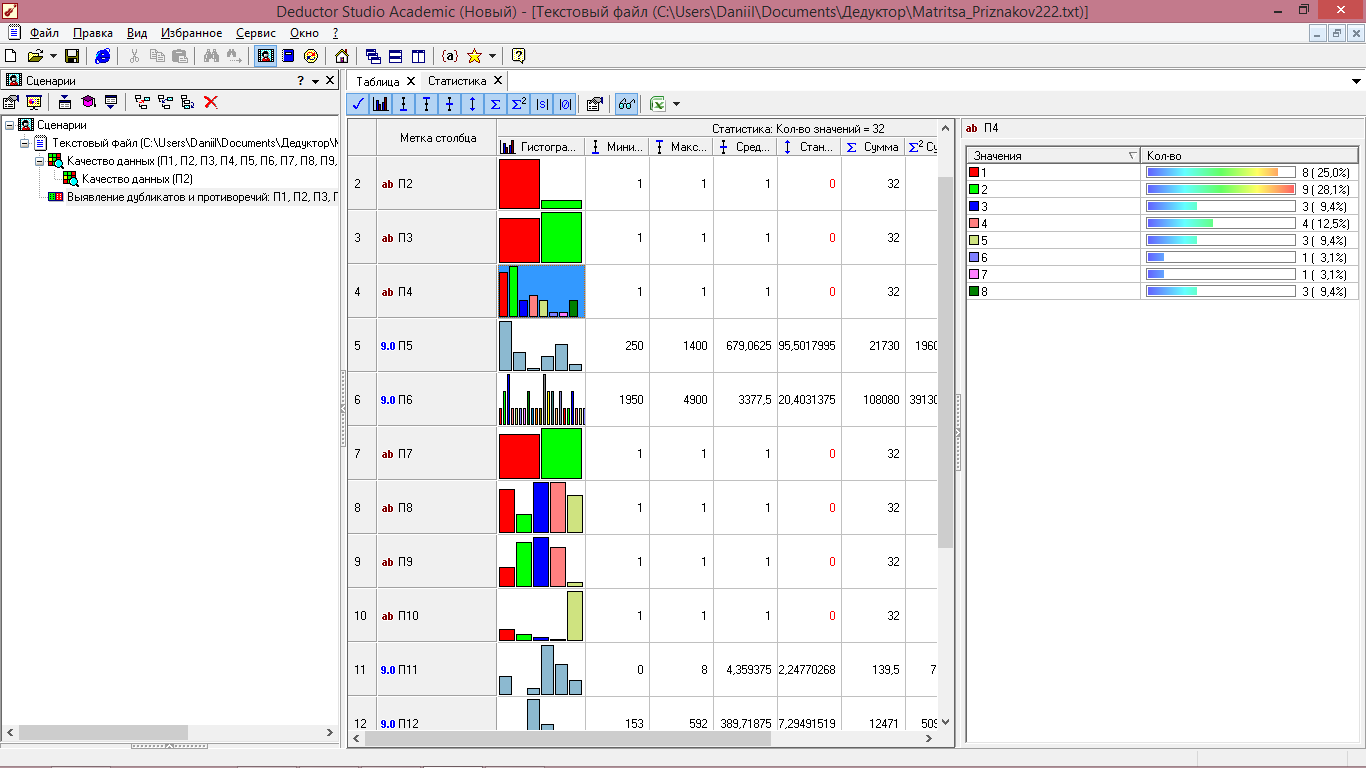
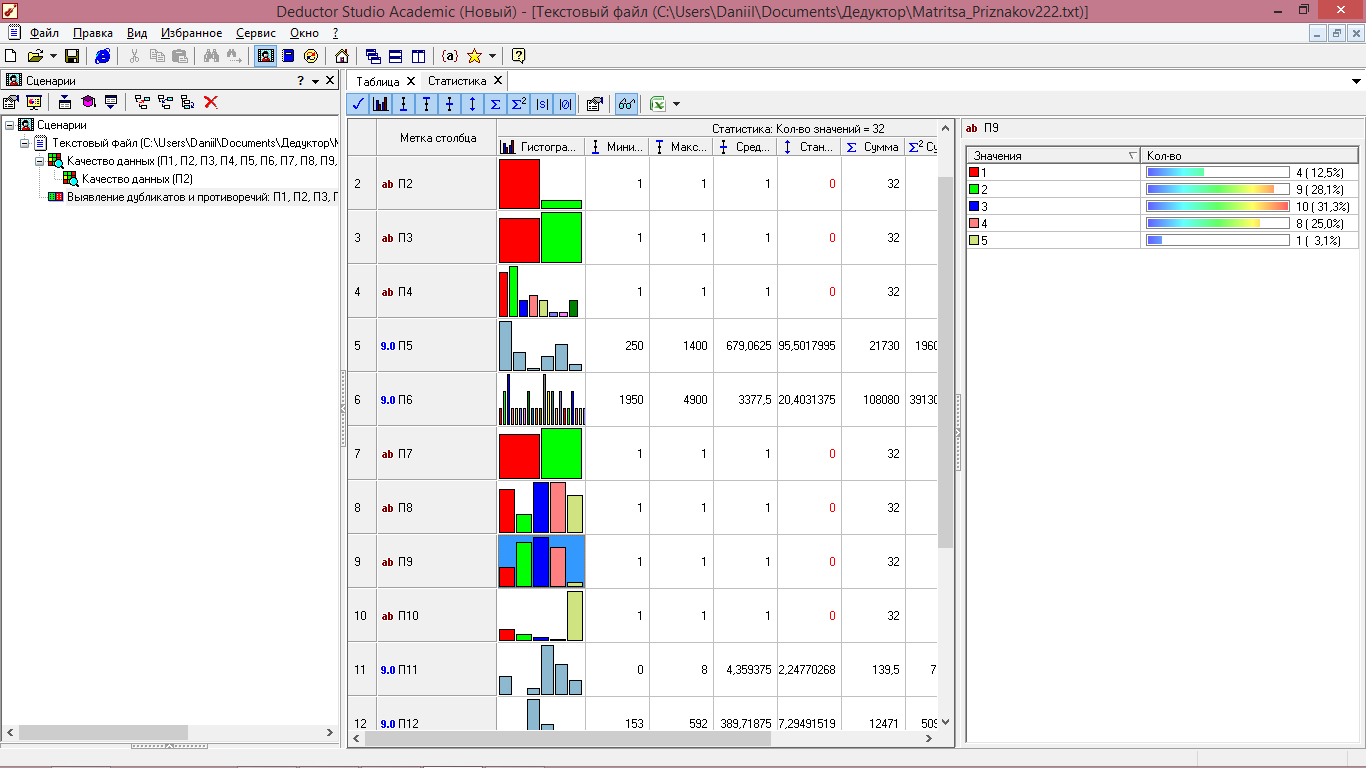
а) б)
Рисунок 5.4 - Частотные таблицы для показателей номинальной шкалы:
П4 (фирма производитель)(а) и П9 (Максимальный диаметр сверления полой коронкой) (б)
Исходя из частотной таблицы показателя П4 (рисунок 5.4 (а)), можем сделать вывод, что 9 шт. или 28,1% всех образцов перфораторов и 8 шт и 25% образцов принадлежат компаниям Bosch и Makita, то есть больше половины рынка принадлежит именно этим компаниям
В частотной таблицы (рисунок 5.4 (б)) показателя П9 (Максимальный диаметр сверления полой коронкой): 10 шт. или 33,3% всех сверлят полой коронкой диаметром 80-90 мм.
Для показателей порядковой шкалы П3 (Тип крепления бура/сверла) также была построена частотная таблица. Исходя из частотной таблицы показателя П3, можем сделать вывод, что 17 образцов масла или 53,1% всех образцов перфораторов снабжены креплениями сверел SDS-Max.
5.2 Анализ взаимосвязей между признаками (корреляционный анализ)
5.2.1 Теоретические сведения
Корреляция (от лат. correlatio - соотношение) – это статистическая взаимозависимость между признаками изучаемого явления. Корреляционный анализ представляет собой математическую процедуру, с помощью которой изучается эта взаимозависимость; он основан на расчете отклонения значений изучаемого признака от линии регрессии (от лат. regression – возврат, в данном случае – возврат к средней) – условной линии, к которой эти значения тяготеют. Чем меньше разброс значений, тем сильнее связи.
Критерии количественной оценки зависимости между переменными называются коэффициентами корреляции или мерами связанности, значения которых служит показателем интенсивности связи.
Следует отметить, что коэффициенты корреляции выражают не причинную (обусловленность одного признака другим), а функциональную (взаимная согласованность изменения признаков) зависимость между признаками. Различают парную (между двумя признаками) и множественную (между несколькими признаками) корреляции.
Две переменные коррелируют между собой положительно, если между ними существует прямое, однонаправленное соотношение. Положительная корреляция соответствует значениям 0 < r <1. Положительную корреляцию следует интерпретировать следующим образом: если значения одной переменной возрастают, то значения другой имеют тенденцию к возрастанию. Чем коэффициент корреляции ближе к 1, тем сильнее эта тенденция, и, наоборот, с приближением коэффициента корреляции к 0 тенденция ослабевает.
Две переменные коррелируют между собой отрицательно, если между ними существует обратное, разнонаправленное соотношение. Отрицательная корреляция соответствует значениям –1 < r < 0. Если значения одной переменной возрастают, то значения другой имеют тенденцию к убыванию. Чем коэффициент корреляции ближе к –1, тем сильнее эта тенденция, и, наоборот, с приближением к 0 тенденция ослабевает.
Для изучения взаимосвязи признаков, измеренных с помощью различных типов шкал, используются разные коэффициенты корреляции. В качестве коэффициента корреляции между переменными, принадлежащими порядковой и номинальной шкалам применяется коэффициент Спирмена. Данный коэффициент равен +1, когда два ряда проранжированы строго в одном порядке, -1, когда два ряда проранжированы в строго обратном порядке, и равен нулю при полном взаимном беспорядочном расположении рангов
Для переменных, принадлежащих к интервальной шкале применяется коэффициент корреляции Пирсона (момент произведений), который равен +1 при строгой (полной) прямой взаимозависимости двух признаков и равен -1 при строгой (полной) обратной взаимозависимости. [6]
5.2.2 Матрица парной корреляции и анализ зависимостей
Так как ПАП «DEDUCTOR» не позволяет составить матрицу парной корреляции, поэтому данная процедура была произведена MS Excel.
1 Шаг – в корреляционном анализе анализируются количественные показатели, поэтому матрица признаков была преобразована (рисунок 5.5).
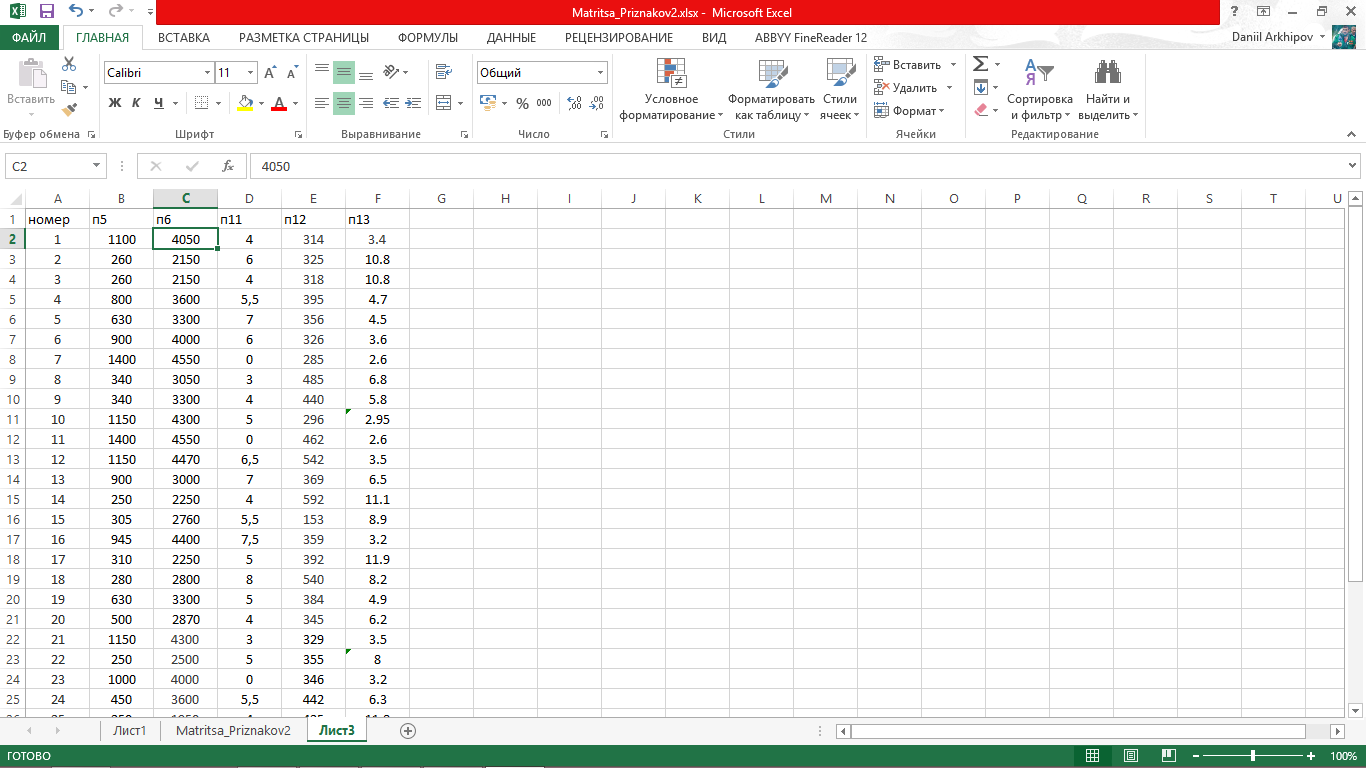
Рисунок 5.5 - Корреляционный анализ (преобразованная матрица данных)
2 Шаг – для того, чтобы составить матрицу парной корреляции, используем функцию «PEARSON», выбирая в качестве значений массива 1 – значения показателя П1, в качестве массива 2 – П1, тем самым определяя коэффициент корреляции (рисунок 5.6).
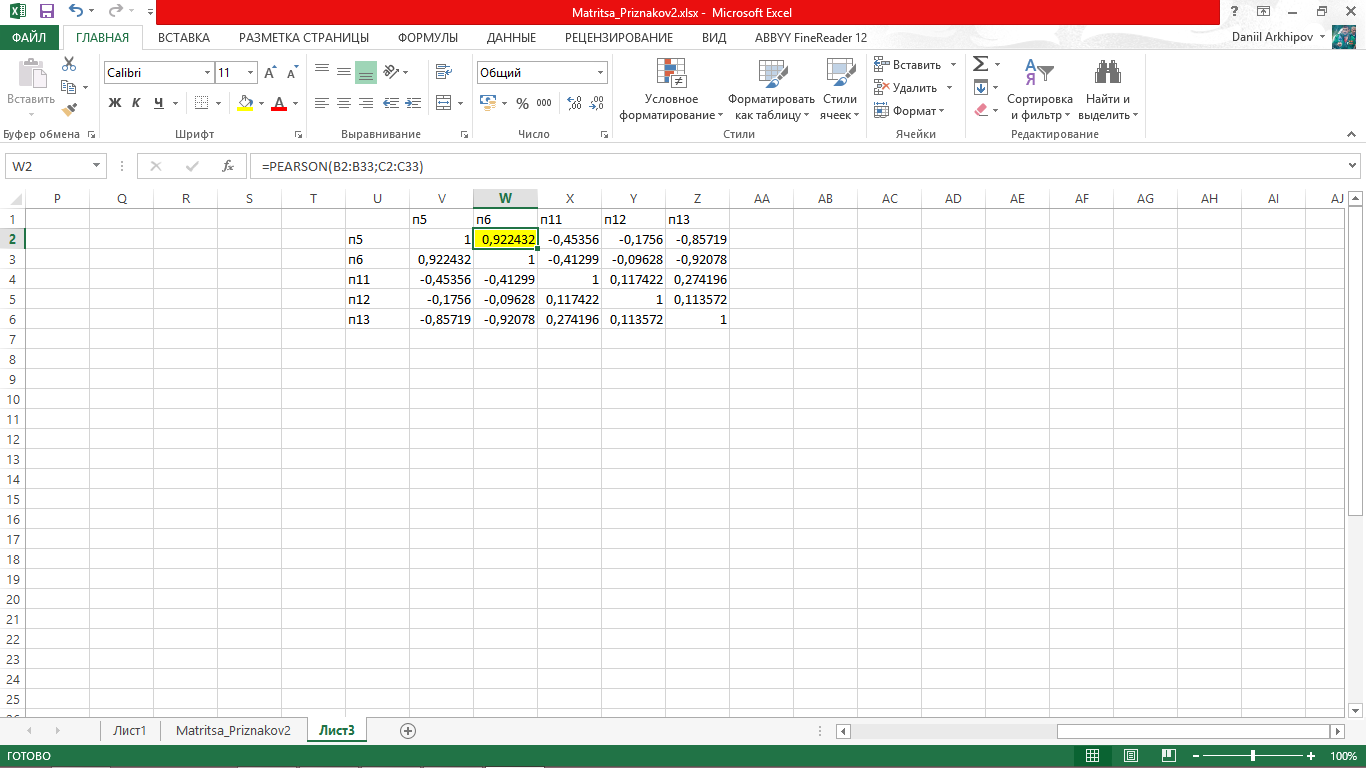
Рисунок 5.6 - Корреляционный анализ (построение матрицы парной корреляции)
3 Шаг - аналогичным образом определяются показатели корреляции каждой пары факторов. Полученная матрица парной корреляции представлена в таблице 5.
Таблица 5 - Матрица парной корреляции
| Показатели | П5 | П6 | П11 | П12 | П13 |
| П5 | 1 | 0,922432 | -0,45356 | -0,1756 | -0,85719 |
| П6 | 0,922432 | 1 | -0,41299 | -0,09628 | -0,92078 |
| П11 | -0,45356 | -0,41299 | 1 | 0,117422 | 0,274196 |
| П12 | -0,1756 | -0,09628 | 0,117422 | 1 | 0,113572 |
| П13 | -0,85719 | -0,92078 | 0,274196 | 0,113572 | 1 |
1.Исходя из полученной матрицы парной корреляции (табл. 5), делаем выход, что самая сильная связь между показателями П5 (Максимальное число оборотов холостого хода) и П6 (Максимальная частота ударов), так как значение коэффициента корреляции, равное 0,92, является максимально высоким в данной базе данных (оно выделено желтым цветом в матрице). Так как данное значение близко к единице, то связь между показателями является сильной.
Исходя из знаний о перфораторах, делаем вывод, что показатель П5 является зависимым от П6 и что данная зависимость является положительной, то есть при увеличении П6 значение П5 увеличивается.
2.Пара «максимальная частота ударов – вес». Связь между параметрами существует, так как коэффициент корреляции равен -0,92. Можно определить данную связь как очень высокую корреляцию. Поскольку коэффициент Пирсона отрицателен, то направление корреляции обратное, т.е. с увеличением значения одного объекта уменьшается значение другого объекта: чем меньше вес, тем выше максимальная частота ударов.
3.Пара «максимальное число оборотов холостого хода – вес». Связь между параметрами существует, так как коэффициент корреляции равен -0,86. Можно определить данную связь как высокую корреляцию. Поскольку коэффициент Пирсона отрицателен, то направление корреляции обратное, т.е. с увеличением значения одного объекта уменьшается значение другого объекта: чем меньше вес, тем выше максимальное число оборотов холостого хода.
4. Пара «максимальное число оборотов холостого хода – длина сетевого кабеля». Связь между параметрами существует, так как коэффициент корреляции равен -0,45. Можно определить данную связь как слабую корреляцию. Поскольку коэффициент Пирсона отрицателен, то направление корреляции обратное, т.е. с увеличением значения одного объекта уменьшается значение другого объекта: чем меньше длина сетевого кабеля, тем выше максимальное число оборотов холостого хода.
5.Пара «максимальная частота ударов – длина сетевого кабеля». Связь между параметрами существует, так как коэффициент корреляции равен -0,41. Можно определить данную связь как слабую корреляцию. Поскольку коэффициент Пирсона отрицателен, то направление корреляции обратное, т.е. с увеличением значения одного объекта уменьшается значение другого объекта: чем меньше длина сетевого кабеля, тем выше максимальная частота ударов.
Для остальных пар присуща очень слабая корреляция.
4 Шаг – для проверки полученной матрицы парной корреляции (табл. 5) проведем корреляционный анализ, используя ПАП «DEDUCTOR». Для этого на панели сценарии выбираем «Мастер обработки» и в открывшемся окне выбираем соответствующий обработчик.
5 Шаг – задаем в качестве входного параметра П5 и в качестве выходного П6, нажимаем «Далее» (рисунок 5.7).
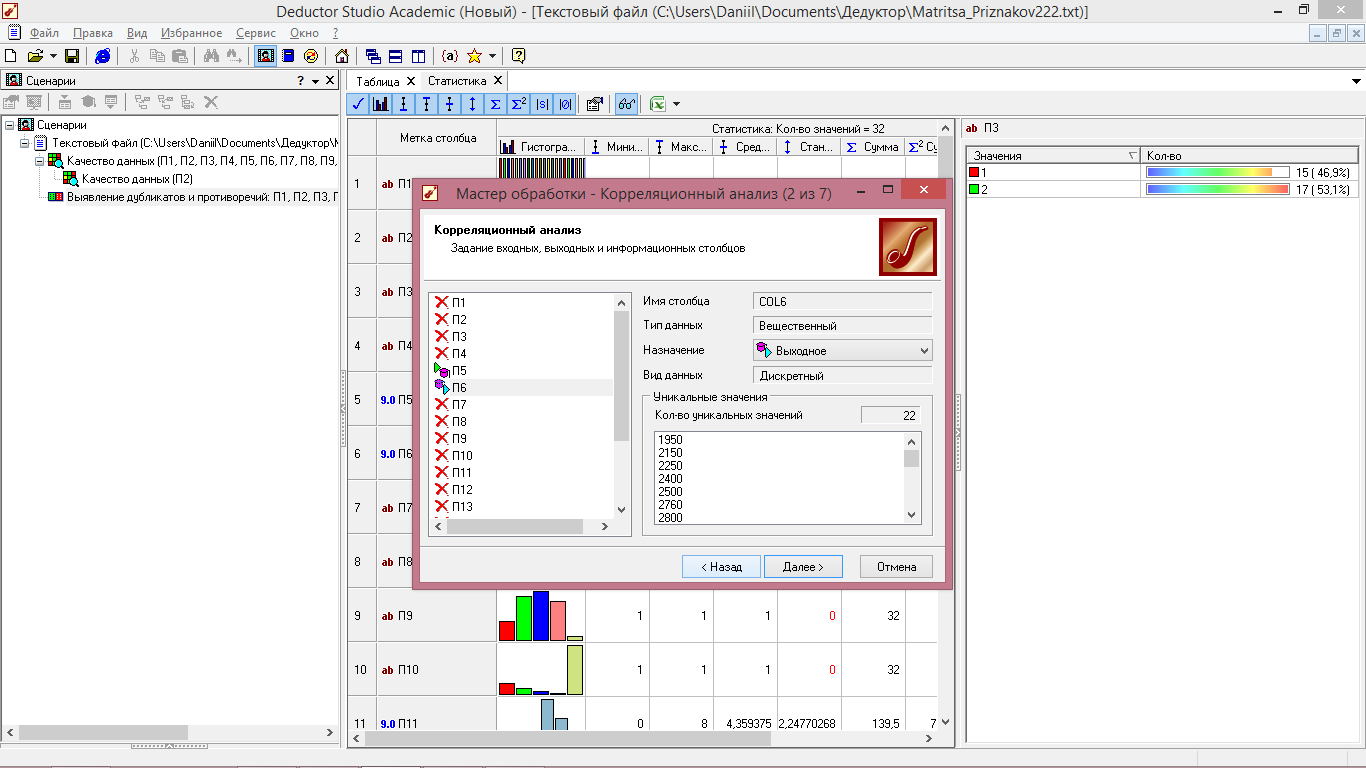
Рисунок 5.7 - Корреляционный анализ (выбор выходных и выходных параметров)
6 Шаг – в качестве метода расчета корреляции выбираем «Коэффициент корреляции Пирсона», при помощи которого можно определить силу и направление линейной зависимости между двумя процессами, происходящими одновременно без учета временного лага.
7 Шаг - нажимаем «Пуск» и ждем, пока в графе «Название процесса» не отобразится «Успешное завершение», а в графе «Процент выполнения текущего процесса» - 100%, после чего нажимаем «Далее»
8 Шаг – ставим галочку напротив значащих факторов и выбираем порог значимости равный 0,05% (рисунок 5.8).
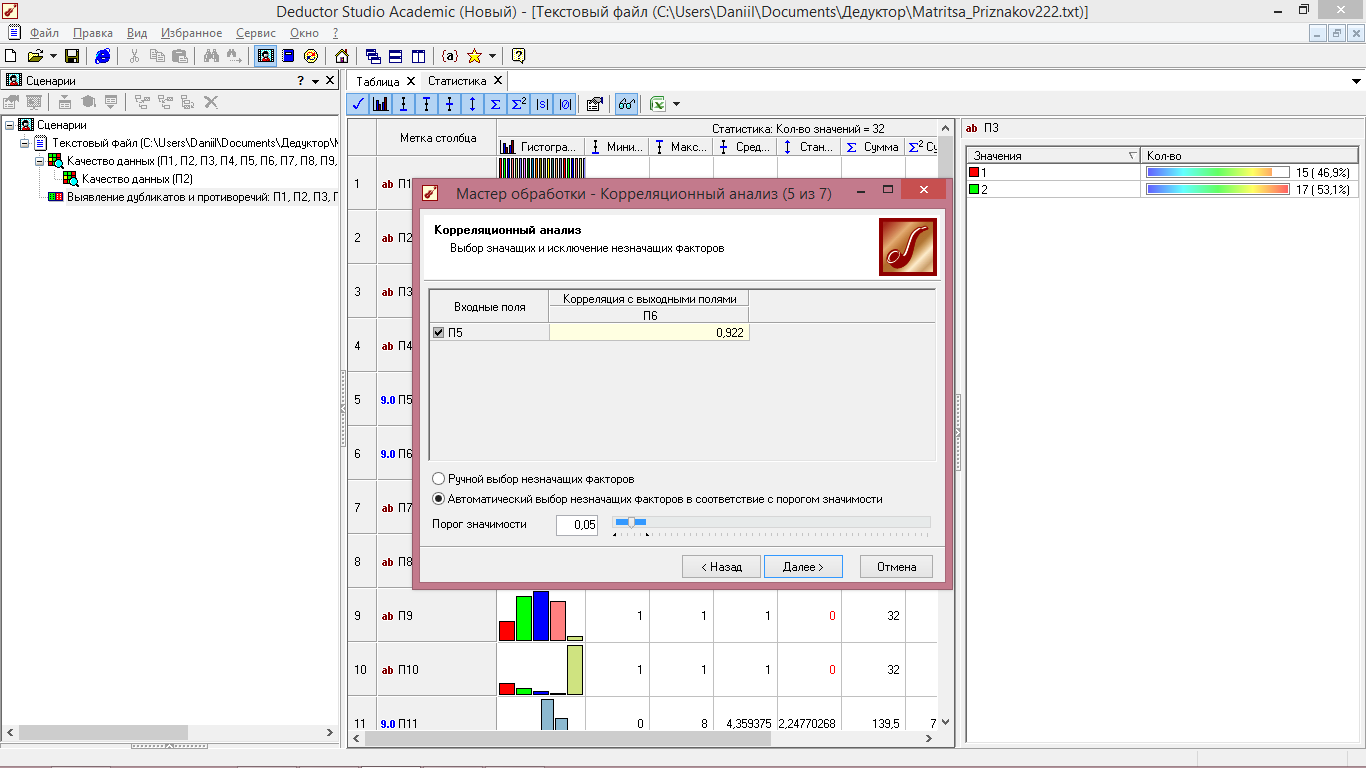
Рисунок 5.8 - Корреляционный анализ (выбор значащих и исключение незначащих факторов)
9 Шаг – выбирая способ отображения данных, ставим галочку напротив «Матрица корреляции. Отображение матрицы корреляции», нажимаем далее (рисунок 35). Присваиваем имя и метку, нажимаем «Готово».
В открывшемся окне отображается коэффициент корреляции (рис. 5.9).
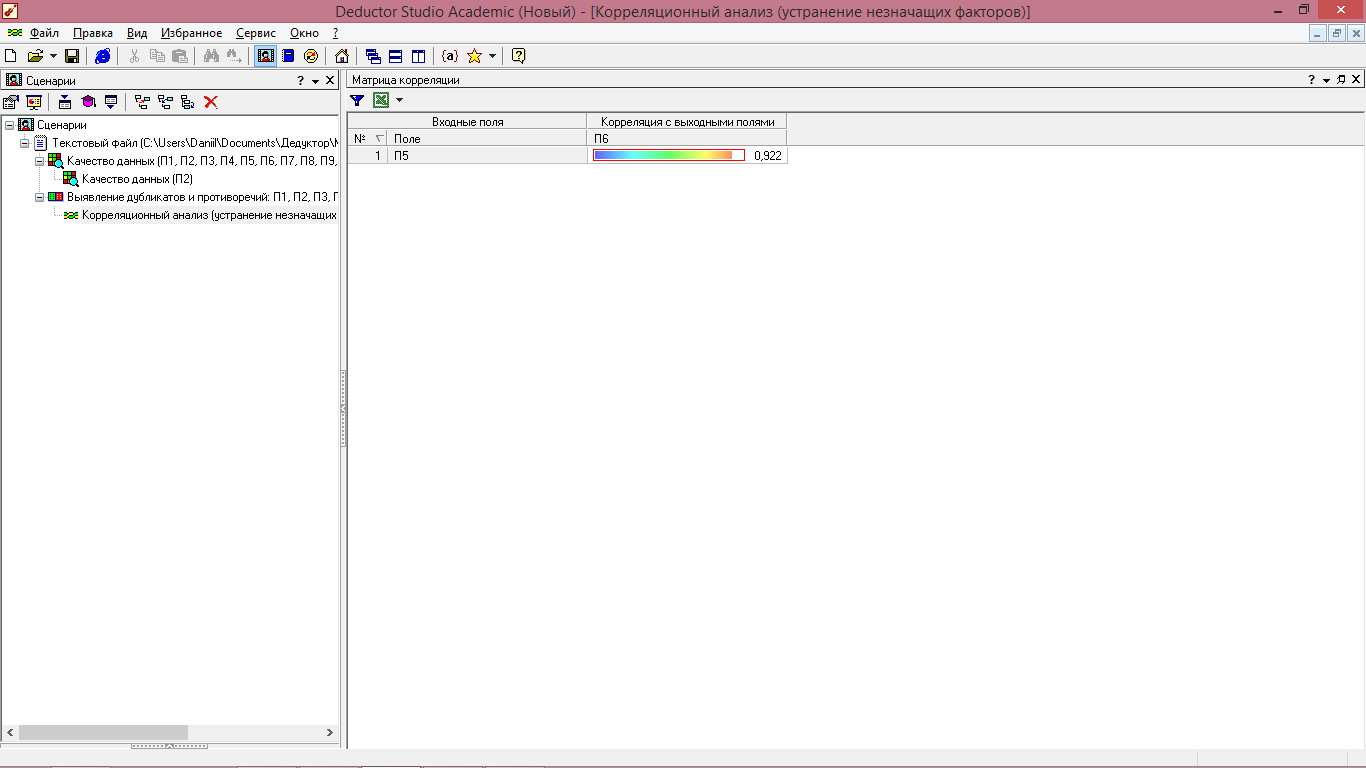
Рисунок 5.9 - Корреляционный анализ (отображение коэффициента корреляции)
Для показателей П5 и П 6 он равен 0,922, аналогичное значение было получено с помощью MS Excel (табл. 5). Делаем выводы, что оба приложения могут быть использованы для построения матрицы парной корреляции.








