Математический маятник

Дата: 2025-05-25; Просмотры: 4

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«Сибирская государственная автомобильно-дорожная академия

(СибАДИ)»

Специальность: Управление качеством

Кафедра: Управление качеством и сервис

Лабораторная работа

по дисциплине «Методы и средства испытания и контроля»

Математический маятник

Выполнила: студентка

группы УКб-14Э1

очная форма обучения

Богочанова А.А.

Проверил: Байда А.С.

Омск – 2016

Лабораторная работа №1

МАТЕМАТИЧЕСКИЙ МАЯТНИК

Цель работы:

Приобретение практических навыков при работе с измерительными приборами. Измерение периода колебаний математического маятника. Изучение метода измерений времени и периода колебаний маятника. Выявление зависимости периода колебаний от длины нити.

Материальное обеспечение:

1. Лабораторный комплекс ЛКМ-3.

2. Модель математического маятника.

1.Теоретические положения

В физике под маятником понимают твёрдое тело, совершающее под действием силы тяжести колебания вокруг неподвижной точки оси. Математическим называют такой маятник, который совершает гармонические колебания. Представляет собой материальную точку, в которой сосредоточена масса тела, совершающего колебания, подвешенную на тонкой невесомой и нерастяжимой нити, закрепленной в неподвижной точке.

Колебания – движения или процессы, обладающие той или иной степенью повторяемости во времени. Колебания называют периодическими, если значения физических величин, изменяющихся в процессе колебания, повторяются через равные промежутки времени.

Амплитуда колебаний – максимальное значение отклонения тела от положения равновесия.

Фаза колебаний – периодически изменяющийся аргумент функции, описывающий колебательный или волновой процесс. Фаза характеризует состояние этого процесса в данный момент времени.

Гармонические колебания – это периодическое изменение во времени физической (или другой) величины, происходящее по закону синуса или косинуса.

Затухающие колебания – собственные колебания, амплитуда которых уменьшается с течением времени.

Период колебаний T – это наименьший промежуток времени, через который система, совершающая колебания, возвращается в первоначальное состояние

Период колебаний измеряется в секундах и определяется следующей зависимостью:

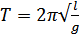, (1)

где l – длина нити; g – ускорение свободного падения.

Частота колебаний – величина, равная числу колебаний, совершаемых в единицу времени

Циклическая (угловая) частота ω является характеристикой гармонических колебаний. Циклическая частота равна числу полных колебаний, совершающихся за 2π единиц времени.

Циклическая частота малых колебаний математического маятника определяется зависимостью:

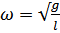, (2)

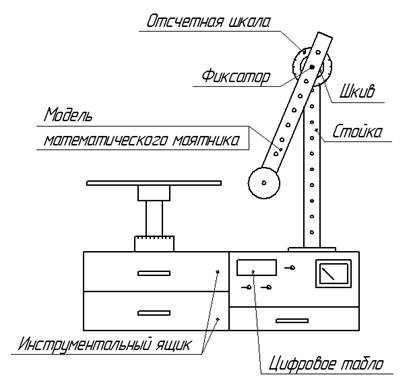
Схема установки модели

математического маятника

2.Результаты измерений и расчетов

Длина подвеса 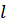, м	Частота	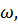Период колебаний Т, с
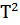
1	2	3	4
0,08	11,07	0,659	0,434
0,10	9,90	0,693	0,480
0,12	9,04	0,736	0,542
0,14	8,37	0,779	0,607
0,16	7,83	0,823	0,677
0,18	7,38	0,867	0,752
0,20	7,00	0,909	0,826
0,22	6,68	0,949	0,901
0,24	6,39	0,988	0,976
0,26	6,14	1,027	1,055
0,28	5,92	1,063	1,130
0,30	5,72	1,101	1,212

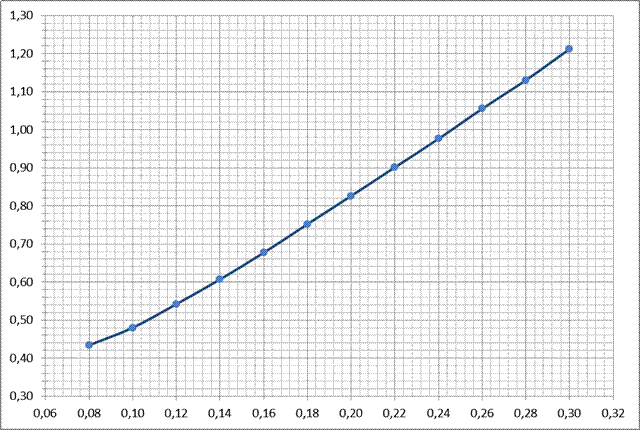
3. График зависимости квадрата периода колебаний от длины подвеса.

Вывод:

В ходе лабораторной работы был измерен период колебания математического маятника и выявлена зависимость периода колебаний от длины нити. В данной лабораторной работе используется модель математического маятника – диск на легкой планке. Планка имитирует нерастяжимую нить, диск значительно тяжелее планки, что имитирует сосредоточение массы в одной точке. С целью получения кратковременных гармонических колебаний амплитуда колебаний маятника ограничена 10º. Было произведено 12 измерений периода колебаний, с последующим измерением длина подвеса увеличивалась на 0,02 м. Из полученных данных можно сделать вывод, что период зависит от длины подвеса: с увеличение длины подвеса увеличивается период колебаний математического маятника. По данным полученным из расчетной формулы (2) можно сделать вывод, что частота математического маятника имеет обратную зависимость: чем короче длина подвеса математического маятника, тем больше частота. По полученным данным был построен график зависимости квадрата периода колебаний от длины подвеса. Графиком зависимости квадрата периода колебаний от длины подвеса является прямая линия, так как квадрат периода колебаний прямо зависит от длины нити, такой вывод можно сделать исходя из формулы (1).