Исследование колебаний балки
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«Сибирская государственная автомобильно-дорожная академия
(СибАДИ)»
Специальность: Управление качеством
Кафедра: Управление качеством и производственными системами
Лабораторная работа
по дисциплине «Методы и средства испытания и контроля»
ИССЛЕДОВАНИЕ КОЛЕБАНИЙ БАЛКИ
Выполнила: студентка
группы УКб-14Э1
очная форма обучения
Богочанова А.А.
Проверил: Байда А.С.
Омск – 2016
Лабораторная работа №3
ИССЛЕДОВАНИЕ КОЛЕБАНИЙ БАЛКИ
Цель работы
Приобретение практических навыков при работе с измерительными приборами. Изучение методик определения модуля Юнга: по колебаниям балки, по смещению при изгибе.
Материальное обеспечение
1. Лабораторный комплекс ЛКМ-3.
2. Цилиндрический кронштейн, нить, подвеска с грузом.
3. Набор цилиндрических стержней
1.Теоретические положения
Деформация – изменение взаимного расположения частиц материальной среды, которое приводит к изменению формы и размеров тела. Простейшие деформации: растяжение, сжатие, изгиб, кручение. Деформация называется упругой, если она полностью исчезает после прекращения действия, вызвавшей ее внешней силы. Пластической называется деформация, не исчезающая полностью после прекращения действия пластических сил и приводящая к необратимым изменениям в структуре твердого тела. При пластической деформации тело не восстанавливает полностью своих прежних размеров и формы.
Закон Гука для упругих деформаций сжатия – растяжения: модуль силы упругости, возникающей при деформации, прямо пропорционален абсолютному удлинению:
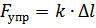 , (1)
, (1)
где k – коэффициент жесткости; Δl – абсолютное удлинение (деформация).
Коэффициент жесткости k – величина, характеризующая упругие свойства тела, равная отношению силы упругости, возникающей при деформации тела, к абсолютному удлинению. Размерность коэффициента жесткости в СИ – ньютон на метр [Н/м].
Модуль упругости E – величина, характеризующая упругие свойства материалов при малых деформациях. При упругой деформации стержня модуль упругости называют модулем Юнга.
Относительное удлинение ε – величина, показывающая, какую часть от длины недеформированного тела составляет изменение длины тела при деформации. Относительное удлинение равно отношению абсолютного удлинения тела к его длине в недеформированном состоянии.
Механическое напряжение σ – величина, характеризующая состояние деформированного тела, равная отношению модуля силы упругости, возникающей в теле при деформации, к площади поперечного сечения деформируемого тела. При этом считают, что сила перпендикулярна сечению тела.
Для круглого стержня с неподвижным закреплением («заделкой») одного конца коэффициент жесткости рассчитывается по формуле:
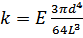 , (2)
, (2)
где k – коэффициент жесткости стержня; E – модуль Юнга; d – диаметр стержня; L – длина стержня от точки «заделки» до точки крепления нити.
Для определения модуля Юнга может быть использован метод расчета коэффициента жесткости стержня без учета массы стержня и шкива (метод 1). Этот метод основан на изменении периода колебаний в зависимости от массы подвешенного груза.
Значение коэффициента жесткости стержня определяется зависимостью:
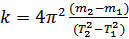 , (3)
, (3)
Где 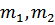 – массы грузов, подвешенных к стержню;
– массы грузов, подвешенных к стержню;
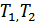 – периоды колебаний стержня при массах
– периоды колебаний стержня при массах 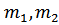
Период колебаний T – это наименьший промежуток времени, через который система, совершающая колебания, возвращается в первоначальное состояние.
Модуль Юнга может быть определен по смещению (деформации) стержня (метод 2). Для этого определяют смещение нижней точки подвески с грузом, при изменении массы груза на некоторое значение Δm.
Коэффициент жесткости стержня определяется зависимостью:
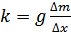 , (4)
, (4)
где g – ускорение свободного падения; Δx – изменение смещения нижней точки подвески; Δm – изменение массы груза .
Модуль Юнга – механическая характеристика конструкционных материалов.
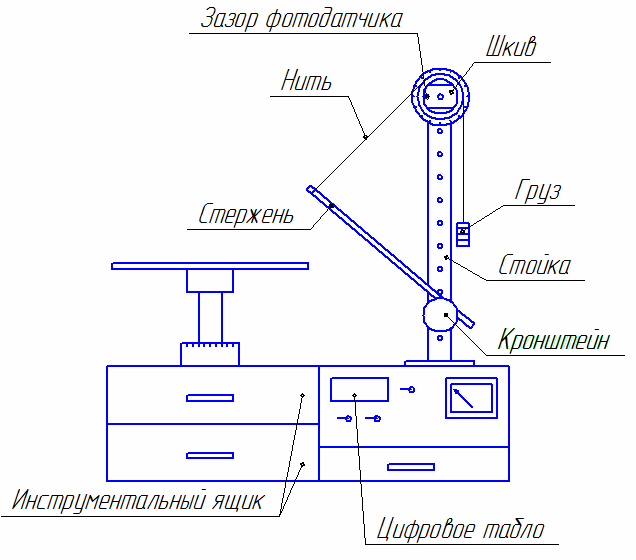
Рис. 1. Схема установки стержня с наборным грузом
Таблица 1. Определение модуля Юнга (метод 1)
|
Показатель | Материал | |
| Латунь | Сталь | |
| Диаметр стержня d, м | 0,004 | 0,004 |
| Длина стержня L, м | 0,284 | 0,293 |
Масса груза 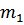 , кг , кг
| 0,150 | 0,150 |
Масса груза 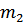 , кг , кг
| 0,200 | 0,200 |
Период колебаний 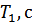
| 0,210 | 0,170 |
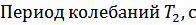
| 0,233 | 0,194 |
Коэффициент жесткости 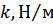
| 193,7 | 225,9 |
Модуль Юнга E, 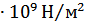
| 117,7 | 150,7 |
Таблица 2. Определение модуля Юнга (метод 2)
| Показатель | Материал | |
| Латунь | Сталь | |
Масса груза 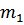 , кг , кг
| 0,150 | 0,150 |
Масса груза 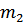 , кг , кг
| 0,200 | 0,200 |
Смещение 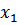 , м , м
| 0,256 | 0,268 |
Смещение 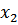 , м , м
| 0,259 | 0,270 |
Смещение 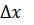 , м , м
| 0,003 | 0,002 |
Коэффициент жесткости 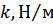
| 163,3 | 245 |
Модуль Юнга E, 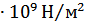
| 99,2 | 163,5 |
Вывод:
В ходе лабораторной работы на установке был измерен период колебания двух стрежней из разных материалов (латунь и сталь). Так же был измерен диаметр этих стержней и их длина от точки подвеса. Из полученных значений периода колебаний был рассчитан коэффициент жесткости, т.е. величина, характеризующая упругие свойства тела. Для расчета Модуля Юнга было использовано два метода. Первый метод расчета коэффициента жесткости стержня без учета массы стержня и шкива. Этот метод основан на изменении периода колебаний в зависимости от массы подвешенного груза. По второму методу Модуль Юнга был определен по смещению стержня. Для этого определяют смещение нижней точки подвески с грузом, при изменении массы груза на некоторое значение Δm. Полученные значения немного отличаются от табличных, но находятся в пределах допустимой погрешности. Значения, полученные разными методами, различаются, но близки к табличным значениям.








