Урок геометрии «Элементы симметрии правильных многогранников»
Цель: ознакомить учащихся с симметрией и ее видами в пространстве.
Задачи:
образовательные:
· ознакомить учащихся с основными видами симметрии в пространстве и её элементами;
· показать возможности использования понятия «симметрия» в математике, химии, физике, биологии.
развивающие:
· развивать познавательную активность и творческие способности;
· активизировать самостоятельную деятельность.
воспитательные:
· воспитывать коммуникативность учащихся.
План урока (45 мин):
1. Организационный момент (3 мин)
2. Изучение нового материала (5 мин) + Практикум (5 мин)
3. Использования понятия «симметрия» в других областях (5 мин)
4. Фронтальный опрос (3 мин) +Симметрия куба – демонстрация (4 мин)
5. Закрепление нового материала (5 мин)
6. Проверочная работа (7 +1мин)
7. Итог урока (рефлексия) (4 мин)
Ход урока:
«Раз, стоя перед черной доской и рисуя на ней мелом разные фигуры, я вдруг был поражен мыслью: почему симметрия приятна для глаз? Что такое симметрия? Это врожденное чувство, отвечал я сам себе. На чем же оно основано? Разве во всём в жизни есть симметрия?»
Л. Толстой «Отрочество»
1. Организационный момент .
Понятие симметрии проходит через всю многовековую историю человеческого творчества.
1. Изучение нового материала (Слайд)
· Новый словарь русского языка Т.Ф.Ефремовой:
СИММЕТРИЯ - соразмерное, пропорциональное расположение частей чего-л. по отношению к центру, середине.
· Толковый словарь русского языка Д.Н.Ушакова:
СИММЕТРИЯ - пропорциональность, соразмерность в расположении частей целого в пространстве, полное соответствие (по расположению, величине) одной половины целого другой половине.
П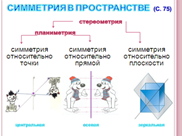 
ростейшими видами пространственной симметрии являются центральная, осевая и зеркальная. (Откройте учебник на с. 75 и ознакомьтесь с данными понятиями в течение 1 мин. Далее, при демонстрации слайдов ученики объясняют особенности видов симметрии – 2 мин)
1 
а) Точки А и А 1 называются симметричными относительно точки О (центр симметрии), если О – середина отрезка АА 1.
1б) Точка О считается симметричной самой себе. (Слайд)
2 
а) Точки А и А 1 называются симметричными относительно прямой (ось симметрии), если прямая проходит через середину отрезка АА 1 и перпендикулярна этому отрезку.
2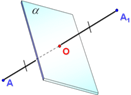 
б) Каждая точка прямой а считается симметричной самой себе. (Слайд)
3а) Точки А и А1 называются симметричными относительно плоскости (плоскость симметрии), если эта плоскость проходит через середину отрезка АА1 и перпендикулярна этому отрезку.
3б) Каждая точка плоскости считается симметричной самой себе. (Слайд)
В 
ывод (учащиеся записывают в тетрадь - 1 мин):
Точка (прямая, плоскость) называется центром (осью, плоскостью) симметрии фигуры, если каждая точка фигуры симметрична относительно нее некоторой точке той же фигуры.
Если фигура имеет центр (ось, плоскость) симметрии, то говорят, что она обладает центральной (осевой, зеркальной) симметрией. (Слайд с анимацией)
Практикум (5 мин)
Задание (работа 3 учеников у доски, остальные учащиеся выполняют работу в тетрадях):
1. Сколько осей симметрии имеют каждая из фигур? (Множество, три, ни одной)
2. Начертите окружность, правильный треугольник и многоугольник используя осевую и центральную симметрию.
1. Я предлагаю вам рассмотреть проявление этой идеи в различных областях науки.