Изображения Леонардо да Винчи додэкаэдра методом жестких ребер (а) и методом сплошных граней (б) в книге Л. Пачоли «Божественная пропорция».
Техника, разработанная Леонардо, являет собой блестящий пример геометрической иллюстрации, нового способа графического изображения научной информации. Эта техника впоследствии многократно использовалась художниками, скульпторами и учеными. В качестве примеров приведем изображение платоновых тел (рис. а) на титульном лист изданной во Франции в 1560 г. книги Жана Кузена «Livre de Perspective» («Книга о перспективе») и надгробный памятник Сэру Томасу Джорджсу (рис. 6), установленный в 1635 г. в кафедральном соборе в Солсбери (Англия).
Рис.4.
Художественное изображение многогранников
в разработанной Леонардо технике
жестких ребер:

а — титульный лист
книги Ж. Кузена
«Книга о перспективе»,

б — надгробный памятник
в кафедральном соборе Солсбери.
Ярчайшим примером художественного изображения многогранников в XX веке являются, конечно, графические фантазии Маурица Эшера (1898-1972), две из которых представлены на рис. 5 (изображая многогранники в этих работах, Эшер пользуется как техникой сплошных граней, так и методом жестких ребер Леонардо).


Рис. 5.
Графические фантазии Маурица Эшера:
а — «Звезды» (1948), б — «Рептилии» (1943).
Приведем также пример изображения многогранника, выполненного художникам Сальвадором Дали (1904-1989) в картине "Тайная вечеря".

Рис. 12.
Сальвадор Дали. Тайная вечеря (1955).
4б) Среди ученых, исследовавших многогранники, особое место принадлежит Иоганну Кеплеру (1571-1630). Кеплер определил классы многогранников, в частности тот, который мы называем архимедовыми телами, описал каждый из многогранников того или иного класса (некоторые — впервые). Еще в молодые годы им овладела идея поиска симметрии или гармонии мира. В своей первой работе "Космогоническая тайна" (1596) Кеплер, опираясь на геометрию, решил вывести число орбит, их относительные размеры и характер движения планет, т. е. проникнуть в замысел творца. Эта работа принесла ему большой успех и широкую известность. В ней ученый вывел свой геометрический принцип, по которому с помощью пяти правильных многогранников - так называемых платоновых тел - обьясняется число известных тогда планет (Меркурий, Венера, Земля, Марс, Юпитер, Сатурн) и относительные размеры их орбит. Геометрия Солнечной системы по Кеплеру заключалась в следующем: вокруг сферы, на поверхности которой по окружности большого круга движется Меркурий, описывается октаэдр; вокруг октаэдра – сфера, на которой находится Венера; вокруг последней сферы описывается икосаэдр и вокруг него сфера, на которой оказывается Земля; Далее идет додекаэдр со сферой, на которой движется Марс; затем тетраэдр со сферой Юпитера; затем следует куб со сферой, на которой находится последняя известная Кеплеру планета – Сатурн. Такая модель гелиоцентрической системы мира получила название "космический кубок". Кеплер считал геометрию "прообразом красоты мира" и в отличие от пифагорейцев искал первопричины не в числовых соотношениях, а в скрытых за числами геометрических фигурах.
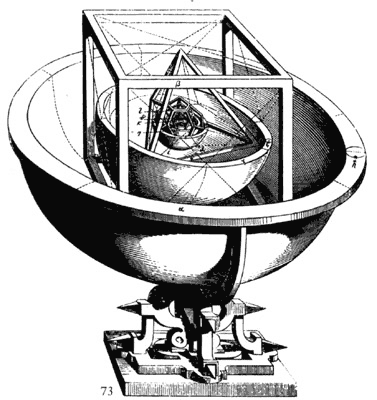
В конце концов, Кеплеру пришлось признать ошибочность этой гипотезы. Позже, изучив долголетние тщательные наблюдения знаменитого астронома Тихо Браге над движением планеты Марс, Кеплер обнаружил, что Марс движется не по кругу, а по эллипсу, и, критически пересмотрев свои взгляды на движение планет, пришел к "законам Кеплера". Ошибочность первоначальной гипотезы, кстати, является красноречивым свидетельством того, что в науке прекрасное (с чисто эстетической точки зрения) все же не всегда оказывается правильным.
5. История изучения и изображения многогранников, уходящая корнями в глубь тысячелетий, продолжается в наши дни, неожиданно «превращаясь» в историю науки о фуллеренах и технологии новых материалов на их основе или историю современной архитектуры. История эта являет собой яркий пример взаимопроникновения различных областей знания, неразрывности понятий «наука» и «искусство» как различных способов познания мира, двух основных составляющих единого целого — культуры, главного наследия человеческой цивилизации.
Домашняя работа. Прочитать п.35,36, посмотреть видеоурок,
проработать учебный материал и решённые задачи учебника в файле, решить задания "Якласс".Задание даётся на неделю, т. к. 09. 05. 2022 г.урока нет.








