Мы начнем наше рассмотрение с правильных многогранников, гранями которых являются равносторонние треугольники.
05. 05. 2022 г. 10 класс. Геометрия.
Тема урока: "Правильные многогранники".
Цели урока: изучение свойств правильных многогранников;
развитие пространственного воображения;
формирование представлений о математике, как универсальном
языке науки, средстве моделирования явлений и процессов;
воспитание культуры личности, отношение к математике как
части общечеловеческой культуры.
Наглядные пособия: модели правильных многогранников и их развертки,
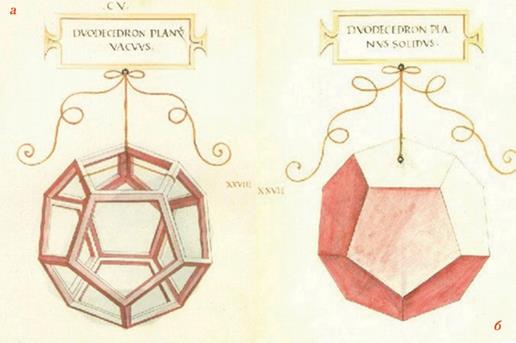
изображения правильных многогранников Леонардо да Винчи,
портрет И. Кеплера, космический кубок И. Кеплера.
План урока
1. Вступительное слово учителя.
2. Определение.
3. а)"Конструирование" правильных многогранников.
б) Разверти правильных многогранников.
4. Выступления учащихся.
а) Многогранники и искусство.
б) Гармония Иоганна Кеплера.
5. Заключение.
6. Домашнее задание
Ход урока
1. Увлекательный раздел геометрии – теория многогранников. Многогранники выделяются необычными свойствами, красивыми формами, которые находят широкое применение в конструировании сложных и красивых многогранных поверхностей для реальных архитектурных сооружений. Сегодня мы познакомимся с правильными многогранниками. Начнем с определения.
2. Определение. Правильным называется многогранник, гранями которого служат одноименные правильные многоугольники, при этом в каждой вершине сходится одинаковое число граней.
3а. Вместе с учащимися "конструируем" правильные многогранники. Выясняем, почему нельзя построить правильный многогранник, гранями которого служат: а)правильные треугольники, при этом в каждой вершине сходится 6 граней; б) правильные четырехугольники, при этом в каждой вершине сходится более 4 граней; в) правильные пятиугольники, при этом в каждой вершине сходится более 4 граней. ( Учащиеся ссылаются на следующее свойство : сумма плоских углов многогранного угла меньше 360°.)
Мы начнем наше рассмотрение с правильных многогранников, гранями которых являются равносторонние треугольники.
Первый из них – тетраэдр. В тетраэдре три равносторонних треугольника встречаются в одной вершине; при этом их основания образуют новый равносторонний треугольник. Тетраэдр имеет наименьшее число граней среди Платоновых тел . 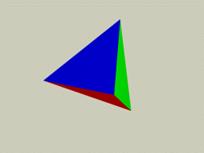

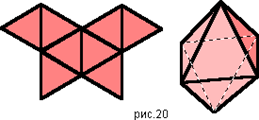
Следующее тело, которое образуется равносторонними треугольниками, называется октаэдром. В октаэдре в одной вершине встречаются четыре треугольника

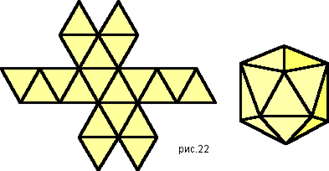
Теперь можно попробовать соединить в одной точке пять равносторонних треугольников. В результате получится многогранник с 20 треугольными гранями – икосаэдр.
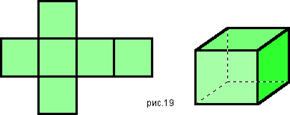
Следующая правильная форма многоугольника – квадрат. Если соединить три квадрата в одной точке и затем добавить еще три, мы получим совершенную форму с шестью гранями, называемую гексаэдром или кубом («Земля»). 
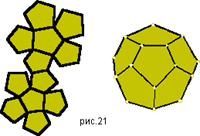
Наконец, существует еще одна возможность построения правильного многогранника, основанная на использовании следующего правильного многоугольника – правильного пятиугольника - пентагона. Если собрать 12 правильных пятиугольников таким образом, чтобы в каждой точке встречалось три пентагона, то получим еще один многогранник – додекаэдр. 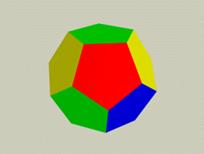
Делаем вывод: можно сконструировать только пять правильных многогранников. Это тетраэдр, куб, октаэдр, икосаэдр и додэкаэдр.
В таблице представлены параметры, полностью характеризующие эти многогранники, в том числе характеристика Эйлера.
Многогранник
Число сторон
грани, m
Число граней,
сходящихся
в каждой
вершине, n
Число
граней, Г
Число
ребер, Р
Число
вершин, В
Г+В-Р
тетраэдр
3
3
4
6
4
2
куб
4
3
6
13
8
2
октаэдр
3
4
8
12
6
2
икосаэдр
3
5
20
30
12
2
додэкаэдр
5
3
12
30
20
2
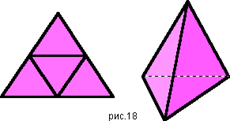
3б. Рассмотреть развертки некоторых правильных многогранников.
4а. Леонардо да Винчи иллюстрировал книгу его современника, математика Луки Пачоли (1445-1514) «Божественная пропорция» («De Devina Proportione»), изданной в 1509 г. Он выполнил 59 иллюстраций различных многогранников, используя впервые метод жестких ребер. Книга оказала большое влияние на развитие геометрии того времени, в частности, стереометрии многогранников. Гравюру с изображением усеченного икосаэдра (рис. 2) Леонардо предваряет надписью по латыни Ycocedron Abscisus (усеченный икосаэдр) Vacuus. Термин Vacuus обозначает тот факт, что грани многогранника изображены «пустыми» — не сплошными. Строго говоря, грани не изображаются вовсе, они существуют только в нашем воображении. Зато ребра многогранника изображены не геометрическими линиями (которые,как известно, не имеют ни ширины, ни толщины), а жесткими трехмерными сегментами. Обе эти особенности данной гравюры и составляют основу способа пространственного изображения многогранников, изобретенного Леонардо для иллюстрации книги Луки Пачоли и называемого сегодня методом жестких (или сплошных) ребер. Такая техника позволяет зрителю, во-первых, безошибочно определить, какие из ребер принадлежат передним, а какие — задним граням многогранника (что практически невозможно при изображении ребер геометрическими линиями), и, во-вторых, взглянуть как бы сквозь геометрическое тело, ощутить его в перспективе, глубине, которые теряются при использовании техники сплошных граней (см. рисунок ).