«Смежные и вертикальные углы».
04. 10. 2022 г. 7 класс. Геометрия.
«Смежные и вертикальные углы».
Цели:
1. Общеобразовательные:
· систематизация знаний, умений и навыков учащихся по данной теме;
2. Развивающие:
· развитие логического мышления, творческой деятельности учащихся;
· развивать умения применять теоретический материал при решении задач.
· развивать внимание и память, умение анализировать, сравнивать и обобщать;
· прививать интерес к геометрии.
· способствовать развитию инициативы и самостоятельности в деятельности
3. Воспиттательные:
· формировать навык анализа и оценки своей деятельности;
· активизировать их творческое мышление;
· воспитание познавательной активности учащихся.
Тип урока: обобщение и систематизация знаний.
ХОД УРОКА
I. Организационный момент
Почти все великие ученые древности и средних веков были выдающимися геометрами. Древнегреческий философ Платон, проводивший беседы со своими учениками в роще “Академа”, одним из девизов своей школы провозгласил: “ Не знающие геометрии не допускаются!”
II . Актуализация знаний учащихся.
Теоретическая разминка.
| 1 У | Г | О | Л | ||||||||||
| 2 В | Е | Р | Т | И | К | А | Л | Ь | Н | Ы | Е | ||
| 3 О | Т | Р | Е | З | О | К | |||||||
| 4 С | М | Е | Ж | Н | Ы | Е | |||||||
| 5 Т | Е | О | Р | Е | М | А | |||||||
| 6 Т | Р | А | Н | С | П | О | Р | Т | И | Р | |||
| 7 Р | А | З | В | Ё | Р | Н | У | Т | Ы | Й | |||
| 8 А | К | С | И | О | М | А | |||||||
| 9 П | Р | Я | М | А | Я |
По горизонтали:
1. Геометрическая фигура, состоящая из точки и двух лучей, исходящих из этой точки.
2. Углы, стороны которых являются продолжениями сторон другого.
3. Часть прямой, заключенная между двумя точками.
4. Углы, у которых одна сторона общая, а две другие являются продолжениями одна другой.
5. Утверждение о свойствах фигур, которые необходимо доказывать.
6. Инструмент для измерения градусной меры угла.
7. Угол, равный 180°.
8. Утверждение о свойствах фигур, которое принимают без доказательства.
9. То, что не имеет ни начала, ни конца.
По вертикали:
( Наука о свойствах геометрических фигур)
Устная работа
1.
|

|
 На рис найдите вертикальные и смежные углы и объясните почему.
На рис найдите вертикальные и смежные углы и объясните почему.
 | |||
 | |||
|
|
|

 2. Исключить неверное высказывание.
2. Исключить неверное высказывание.
|
|

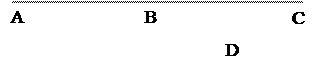 |
1. Ð ABF и ÐFBC – смежные углы
2. Ð ABE и Ð DBC – вертикальные углы
3. Ð EBF и ÐFBC – смежные углы
4. Ð DBC и Ð ЕBF – вертикальные углы
3. Разность двух углов, получившихся при пересечении двух прямых, равна 36°. Доказать, что они не вертикальные.
Доказательство
1. Пусть они вертикальные
2. Тогда по свойству вертикальных углов они равны, т.е. разность равна нулю
3. Получили противоречие с условием, т.к. по условию разность равна 36°
4. Следовательно, они не вертикальные
Лото
| 1. Один из смежных углов – тупой, каким является второй угол? | 2. острый |
| 2. Один из двух углов, который получается при пересечении двух прямых, равен 60°. Чему равны остальные? | 3. 60°, 120°, 120° |
| 3. Острым, тупым или прямым будет угол, смежный с углом в 30о? | 1. тупой |
| 4. Найдите угол смежный с углом 35°. | 9. 1450 |
| 5. Будут ли углы смежными, если один из них равен 20°, а второй 160° и общей частью двух углов является сторона? | 4. Да |
| 6. Может ли сумма трёх углов при пересечении двух прямых равняться 100°? | 7. Нет |
| 7. Один из четырех углов, получившихся при пересечении двух прямых равен 80°. Чему равны остальные углы? | 5. 1000, 80°, 1000 |
| 8. Может ли при пересечении двух прямых образоваться четыре острых угла? | 7. Нет |
| 9. Сумма двух углов равна 200о. Смежные ли это углы? | 7. Нет |
| 10. Найдите угол смежный с углом 90°. | 6. 90° |
| 11. Сумма двух углов равна 180о. Обязательно ли эти углы смежные? | 7. Нет |
| 12. Один из четырех углов, получившихся при пересечении двух прямых равен 140о. Чему равны остальные углы? | 8. 400, 140°, 400 |
| 13. Острым, тупым или прямым будет угол, смежный с углом в 130о? | 2. острый |
Правильный ответ: 2319475776782
Проверка домашнего задания
III. Закрепление знаний и умений.
|
|

|
|
1.
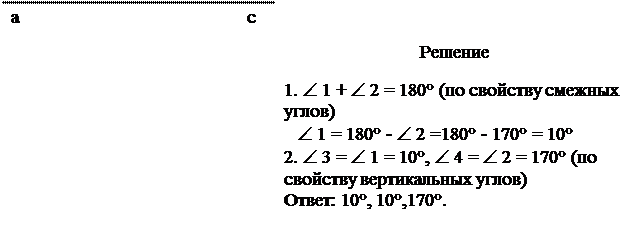 |
|


|
|
|
2.
3.Один из двух углов, который получается при пересечении двух прямых, в 9 раз меньше другого. Найти эти углы.
Решение
1. Пусть х – градусная мера Ð 1.
Тогда 9х – градусная мера Ð 2.
Сумма смежных углов равна 180°
х + 9х = 1800,
10х = 1800,
х = 180
2. Ð 4 = Ð 2 = 180° - 18° = 162°,
3. Ð 3 = Ð 1 = 18°, (по свойству вертикальных углов)
Ответ: 18°, 18°,162°, 162°
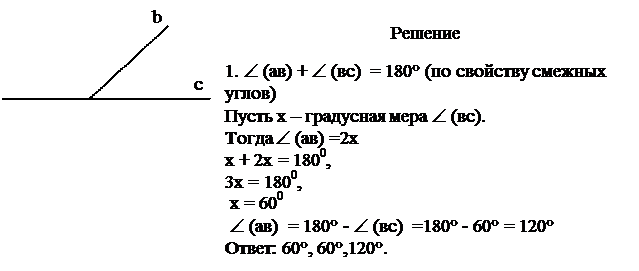
4.
| ||||||
| ||||||
| ||||||
5.
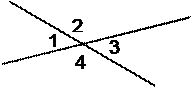 |
Ð 1 + Ð 3 = 80°
|

 6.
6.
| ||||||
| ||||||
| ||||||
IV . Контроль полученных знаний.
Самостоятельная работа.
Вариант 1.
1. Найдите смежные углы, если один из них в 4 раза больше другого.
2. Один из углов, которые получаются при пересечении двух прямых на 20° меньше другого. Найдите эти углы.
Вариант 2.
- Найдите смежные углы, если один из них в 5 раза меньше другого.
- Один из углов, которые получаются при пересечении двух прямых на 40° больше другого. Найдите эти углы.
Ученики сдают тетради с самостоятельной работой.
V . Задание на дом
Составить 2 задачи на тему: «Смежные и вертикальные углы».
V I . Релаксация. Подведение итогов урока.
Закончить наш урок, мне хотелось бы притчей.
Шел мудрец, а навстречу ему три человека, которые везли под горячим солнцем тележки с камнями для строительства. Мудрец остановился и задал каждому по вопросу.
У первого спросил: “Что ты делал целый день?” И тот с ухмылкой отвечает, что целый день возил проклятые камни.
У второго спросил: “ А что ты делал целый день?” А тот ответил: “А я добросовестно выполнял свою работу”.
А третий улыбнулся, его лицо засветилось радостью и удовольствием: “ А я принимал участие в строительстве храма!”
На все окружающее нас, можно смотреть разными глазами, выражать разными словами, но из любой ситуации должны сделать вывод, двигающий нас вперед!








