Брус без нижней опорной поверхности
Министерство науки и высшего образования Российской Федерации
Федеральное государственное автономное образовательное учреждение
высшего образования
«Самарский национальный исследовательский
университет имени академика С.П. КОРОЛЁВА»
(Самарский университет)
Институт ракетно-космической техники
Кафедра сопротивления материалов
Расчётно-проектировочная работа №1
Расчёт статически неопределимого ступенчатого бруса
Вариант № 578
Выполнил: Емелин Н. М., гр.1208
Проверил: Вакулюк В.С.
Самара 2019
Задача
Стальной ступенчатый брус помещён между двумя опорными поверхностями. Один конец его жёстко защемлён в верхней опоре, а нижний находится на расстоянии δ от нижней опорной поверхности. К брусу приложены силы вдоль оси и, кроме того, после нагружения изменяется его температура. Заданы размеры бруса, величины сил и изменение температуры.
Требуется определить нормальные силы N, нормальные напряжения σ, продольные перемещения u на всех участках бруса, построить соответствующие эпюры и подобрать марку стали. Задача решается для двух случаев: без нижней опорной поверхности и при ее наличии.
Реферат
Расчётно-проектировочная работа: 16 стр., 2 рисунка, 3 источника.
СТУПЕНЧАТЫЙ БРУС, НОРМАЛЬНЫЕ СИЛЫ, НОРМАЛЬНЫЕ НАПРЯЖЕНИЯ, ПРОДОЛЬНЫЕ ПЕРЕМЕЩЕНИЯ, УСЛОВИЕ ПРОЧНОСТИ.
Объектом исследования является ступенчатый брус, испытывающий деформацию центрального растяжения (сжатия), в условиях изменяющейся температуры.
Цель работы – определение нормальных сил, нормальных напряжений, удлинений участков бруса, перемещений границ участков ступенчатого бруса и расчёты на прочность.
В результате работы были определены нормальные силы N , нормальные напряжения 𝜎 и продольные перемещения u на всех участках бруса. А так же построены соответствующие эпюры и подобраны марки стали бруса.
Эффективность работы заключается в получении навыков определения удлинения бруса при данных нагрузках и изменениях температур, а так же в подборе марки стали бруса с точки зрения экономичности.
Содержание
1 Введение 5
2 Исходные данные. 6
3 Основная часть. 4
3.1 Брус без нижней опорной поверхности. 7
3.2 Брус c нижней опорной поверхностью.. 11
4 Заключение. 15
5 Список используемых источников. 16
Введение
В данной расчётно-проектировочной работе мы должны определить нормальные силы, нормальные напряжения, удлинение на каждом участке заданного ступенчатого бруса, перемещение границ участков, построить эпюры N, σ, u, из условия прочности подберём марку стали для статически определимого и статически неопределимого бруса.
Исходные данные
Данные по варианту 578.
Стальной ступенчатый брус жёстко защемлён одним концом, другой конец бруса до нагружения находится на расстоянии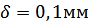 
от опорной поверхности. Он нагружен силами 
, 
, 
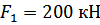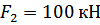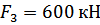, после чего его температура повышается на 
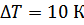. Ступени бруса имеют длину 
, 
, 
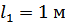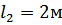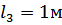, и диаметры 
, 
, 
.
, 
, 
.
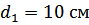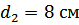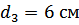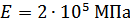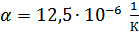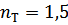Брус без нижней опорной поверхности
Составим уравнение статики для варианта с одной верхней опорной поверхностью:
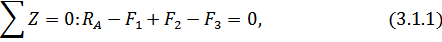
где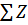 
– сумма всех сил, приложенных по оси z, 
; 
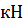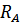– реакция опоры, .
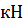Из этого уравнения выразим и найдём :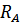
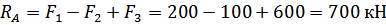
Для определения внутренних усилий разобьём брус на участки, границами которых являются точки приложения сил или сечения, где изменяются диаметры (рис. 1).
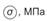
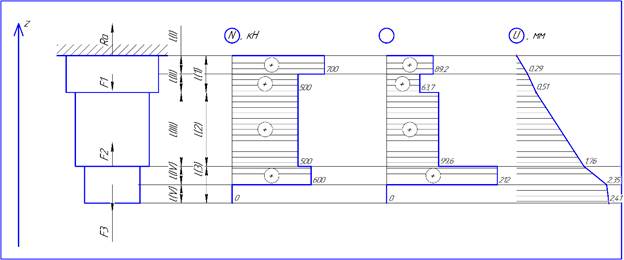
Рисунок 1.
Используя метод сечений и уравнение статики (3.1.1), найдём значения внутренних усилий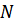 
на каждом участке:
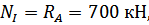
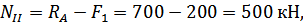
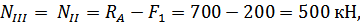
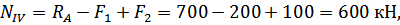
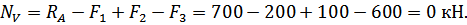
Напряжение в брусе вычисляем по формуле:
где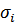 
– напряжение на 
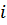-ом участке бруса, 
; 
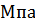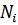– нормальное напряжение на 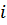-ом участке бруса, ; 
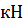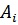– поперечное сечение 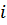-ого участка бруса, 
.
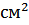Найдём поперечные сечения по формуле:
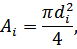
где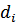 
– диаметр бруса на -ом участке бруса, 
.
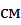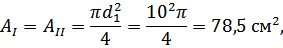
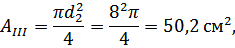
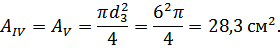
Определяем нормальные напряжения на каждом участке по формуле (3.1.2):
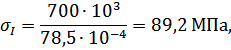
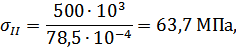
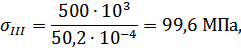
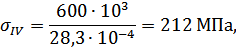
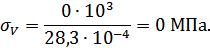
Абсолютные деформации на участках бруса вычисляются по формуле:
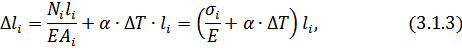
где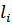 
– длина -ого участка бруса, м.
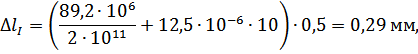
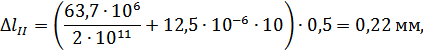
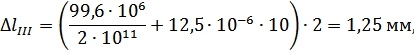
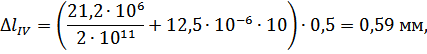
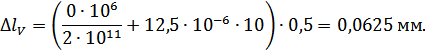
Перемещения сечений бруса вычислим по формуле:
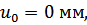
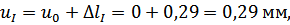
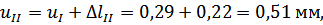
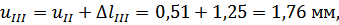
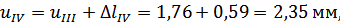
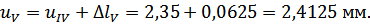
По вычисленным значениям нормальных сил, нормальных напряжений и перемещений построим соответствующие эпюры (рис. 1).
Марку стали назначим из условия прочности при центральном растяжении и сжатии:
где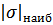 
– модуль наибольшего напряжения, 
; 
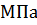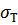– предел текучести, ; 
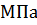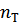– коэффициент запаса текучести.
Из выражения (3.1.5) выразим :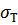
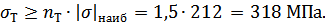
Этому пределу текучести будет соответствовать Сталь 35, у которой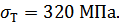 
Брус c нижней опорной поверхностью
Составим уравнение статики для случая с одной верхней и одной нижней опорными поверхностями:
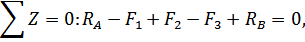
из которого следует, что задача статически неопределима, так как для определения двух неизвестных сил имеем лишь одно уравнение.
Составим уравнение совместности деформаций бруса:
где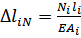 
– удлинение участков бруса от действия нормальных сил, мм; 
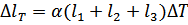– температурное удлинение бруса, мм.
Определим методом сечений нормальные силы на каждом участке бруса:
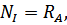
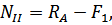
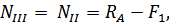
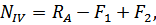
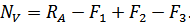
Подставим эти значения нормальных сил в уравнение (3.2.1):
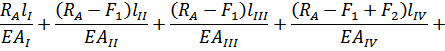
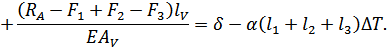
Из этого уравнения следует:
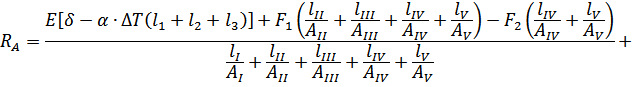
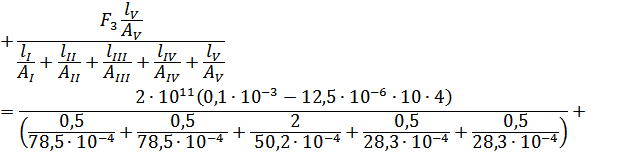
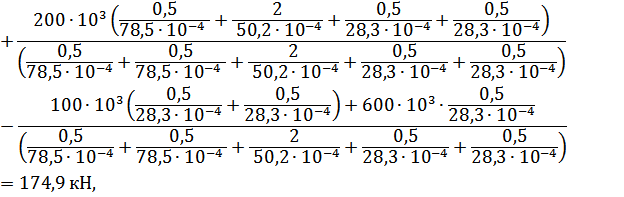
тогда:
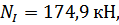
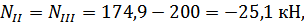
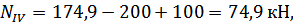
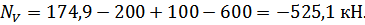
Определяем нормальные напряжения на каждом участке по формуле (3.1.2):
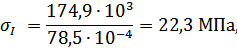
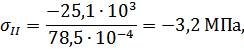
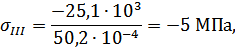
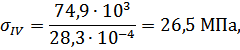
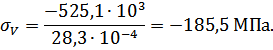
Абсолютные деформации на участках бруса вычисляются по формуле (3.1.3):
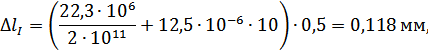
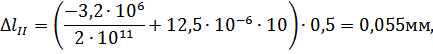
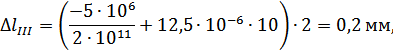
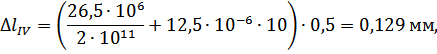
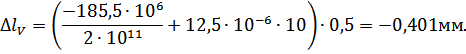
Перемещения сечений бруса вычислим по формуле (3.1.4):
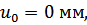
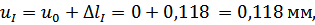
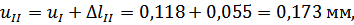
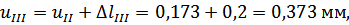
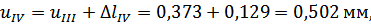
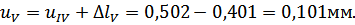
Перемещение нижнего конца бруса должно равняться зазору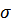 
.
Вычислим погрешность решения:
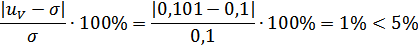
Погрешность в данном случае является допустимой.
По вычисленным значениям нормальных сил, нормальных напряжений и перемещений построим соответствующие эпюры, представленные на рисунке 2.
Марку стали назначим из условия прочности при центральном растяжении, сжатии по формуле (3.1.5):
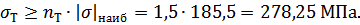
Этому пределу текучести будет соответствовать Стали Ст5, у которой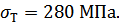 
| |
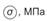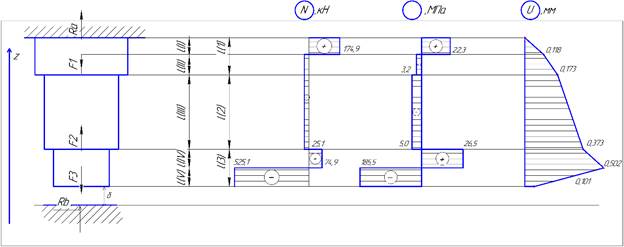
Рисунок 2
Заключение
В результате работы определены нормальные силы, нормальные напряжения, удлинения на каждом участке заданного ступенчатого бруса, перемещения границ участков, построены эпюры N, σ, u, из условия прочности подобрана марка стали.
Задача решена для двух случаев: без нижней опорной поверхности, с нижней опорной поверхностью.
Список используемых источников
1. СТО СГАУ 02068410-004-2007. Общие требования к учебным текстовым документам. – Самара, СГАУ 2007. -34с.
2. Лежин, СМ. Справочные данные к расчётно-проектировочным и курсовым работам по сопротивлению материалов 4.1 [Текст]/СМ. Лежин, А.П. Филатов, Ю.И. Кольцун, В.К. Шадрин. – Самара: СГАУ, 1998.- 27 с.
3. Филатов, А.П. Сборник расчетно-проектировочных работ по сопротивлению материалов [Текст]: Задание и методические указания к расчетно-проектировочным работам / А.П. Филатов, В.К. Шадрин, Ю.И. Кольцун, С.А. Бордаков, В.Б. Иванов.- Самара: СГАУ, 2002.- 36с.