Алгоритм обучения Хэбба

Дата: 2025-05-25; Просмотры: 17

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

По существу Хэбб предположил, что синаптическое соединение двух нейронов усиливается, если оба эти нейрона возбуждены. Это можно представить как усиление синапса в соответствии с корреляцией уровней возбужденных нейронов, соединяемых данным синапсом. По этой причине алгоритм обучения Хэбба иногда называется корреляционным алгоритмом.

Идея алгоритма выражается следующим равенством:

w_ij(t+1) = w_ij(t) + NET_i NET_j,

где w_ij(t) – сила синапса от нейрона i к нейрону j в момент времени t; NET_i – уровень возбуждения предсинаптического нейрона; NET_j – уровень возбуждения постсинаптического нейрона.

Концепция Хэбба отвечает на сложный вопрос, каким образом обучение может проводиться без учителя. В методе Хэбба обучение является исключительно локальным явлением, охватывающим только два нейрона и соединяющий их синапс; не требуется глобальной системы обратной связи для развития нейронных образований.

Последующее использование метода Хэбба для обучения нейронных сетей привело к большим успехам, но наряду с этим показало ограниченность метода; некоторые образы просто не могут использоваться для обучения этим методом. В результате появилось большое количество расширений и нововведений, большинство из которых в значительной степени основано на работе Хэбба.

Метод сигнального обучения Хэбба

Как мы видели, выход NET простого искусственного нейрона является взвешенной суммой его входов. Это может быть выражено следующим образом:

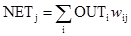
где NET_j – выход NET нейрона j; OUT_i – выход нейрона i;w_ij – вес связи нейрона i с нейроном j.

Можно показать, что в этом случае линейная многослойная сеть не является более мощной, чем однослойная сеть; рассматриваемые возможности сети могут быть улучшены только введением нелинейности в передаточную функцию нейрона. Говорят, что сеть, использующая сигмоидальную функцию активации и метод обучения Хэбба, обучается по сигнальному методу Хэбба. В этом случае уравнение Хэбба модифицируется следующим образом:

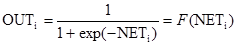
w_ij(t+1) = w_ij(t) + OUT_i OUT_j

где w_ij(t) – сила синапса от нейрона i к нейрону j в момент времени t; OUT_i – выходной уровень пресинаптического нейрона равный F(NET_i); OUT_j – выходной уровень постсинаптического нейрона равный F(NET).