Расчет термодинамических параметров плазмы цинка
Данные о свойствах веществ, находящихся в плазменном состоянии, необходимы для разработки высокоэффективных технологических процессов, создания ряда плазменных устройств высокой плотности энергии, при решении актуальных задач радиационной газовой и плазмодинамики, связанных с исследованием высокотемпературных газодинамических явлений и процессов, и т.д. Мы проведем расчет термодинамических свойств плазмы цинка при температурах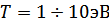 
и плотностях 
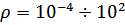. Данный диапазон позволяет обоснованно проводить расчет состава и термодинамических свойств плазмы.
Методика расчета
Парциальный состав многокомпонентной плазмы рассчитывается по системе уравнений Саха-Эккерта с учетом неидеальности и сохранения соотношения между числом частиц различных элементов:
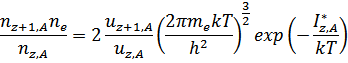
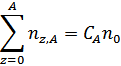
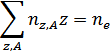
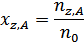
Здесь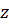 
- остаточный заряд (для отрицательного иона 0), 
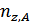-концентрация -ионов элемента 
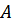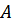; -атомный номер элемента; 
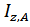-энергия ионизации; 
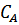-процентное содержание ионов элемента в плазме; 
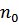-полная концентрация атомов и ионов; 
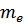-масса электрона; 
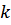-постоянная Больцмана; 
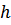-постоянная Планка;
Статистические суммы ионов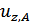 
вычисляются с учетом возбужденных состояний, энергия ионизации и стат.веса которых даны. При этом, суммирование проводится до уровня с энергией ионизации, не превышающей 
.
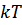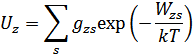
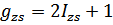
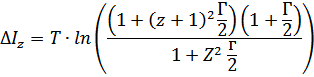
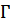- параметр неидеальности;
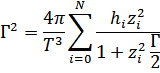
В системе Хартри (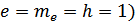 
:
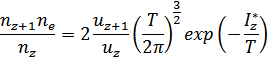
Термодинамические функции- давление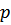 
и внутренняя энергия 
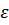- определяются в пренебрежение кулоновскими добавками.
Термодинамические функции плазмы определяются по формулам:
Давление:
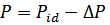
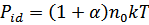
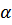- степень ионизации; 
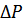- поправка на неидеальность;
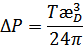
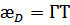
Внутренняя энергия:
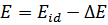
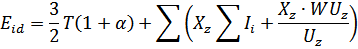
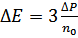- поправка на неидеальность;
Удельная энтропия:
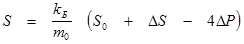
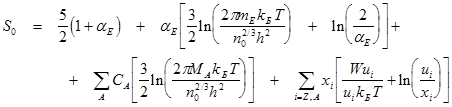
D S , D P - поправки на неидеальность
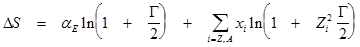
me , MA - массы электрона и атома; h - постоянная Планка; Z - заряд иона.
Удельная энтальпия:
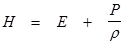
Удельная свободная энергия:
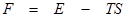
Изохорная теплоемкость:
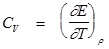
Изобарная теплоемкость:
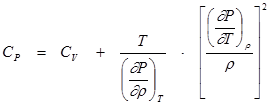
Показатель адиабаты:
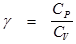
Адиабатная скорость звука:
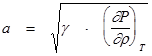
Необходимо отметить, что методика, изложенная выше, может быть использована только для невырожденной атомарной плазмы, находящейся в состоянии термодинамического равновесия и, кроме того, имеет ряд ограничений своей применимости.
Расчетные данные приведены в форме графиков для цинковой плазмы в диапазонах измерения температур 1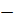 
10эВ и плотностей 
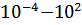кг/м3.
С помощью программы «ТОТ-термодинамика» проведем расчет ионизационного состава и термодинамических свойств (давление, внутренняя энергия, энтропия, энтальпия, изобарная и изохорная теплоемкости, показатели адиабаты, уравнения состояния, скорость звука) цинковой плазмы.
В основу расчета ионизационного состава и термодинамических функций плазмы положено уравнение Саха-Эккерта с учетом неидеальности плазмы в приближении Дебая-Хюккеля в большом каноническом ансамбле. Расчет статсумм проводится с использованием баз данных по энергетическим уровням атомов и ионов элементов, входящих в смесь и «обрезанием» на среднем межчастичном расстоянии с введением экспоненциального форм-фактора.
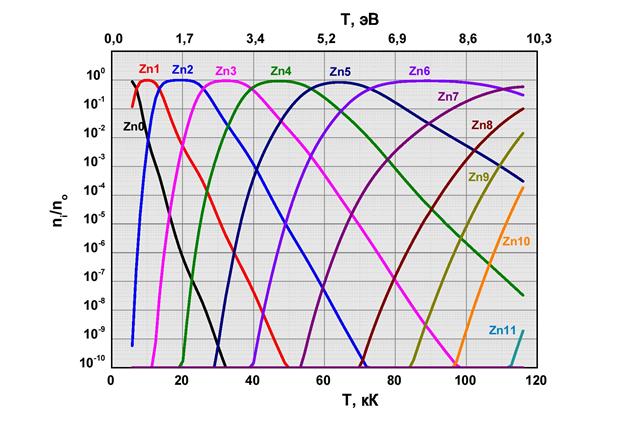
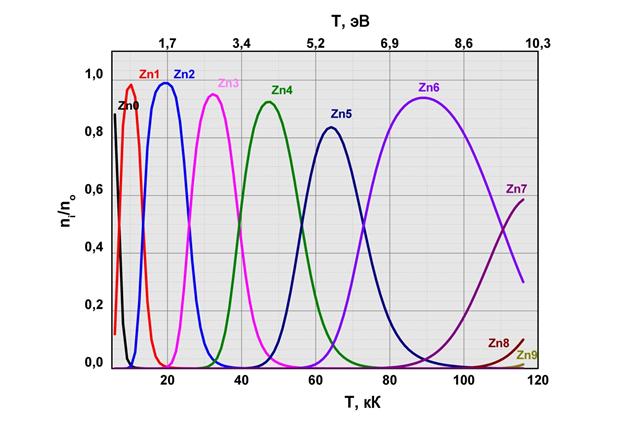
Рис.2.1 Ионизационный состав плазмы цинка при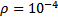 
кг/м3
Термодинамические свойства плазмы цинка
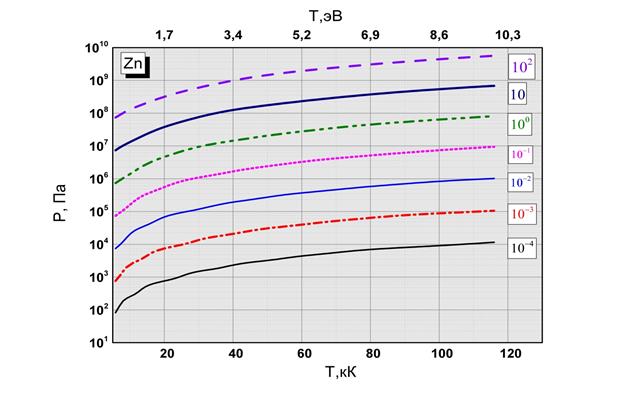Рис.2.2 Зависимость давления от температуры и плотности
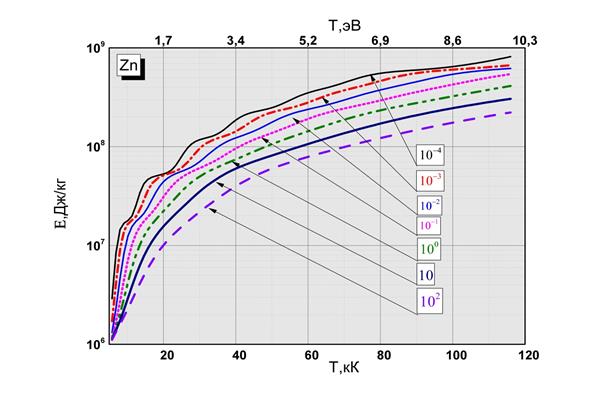
Рис.2.3 Зависимость внутренней энергии от температуры и плотности
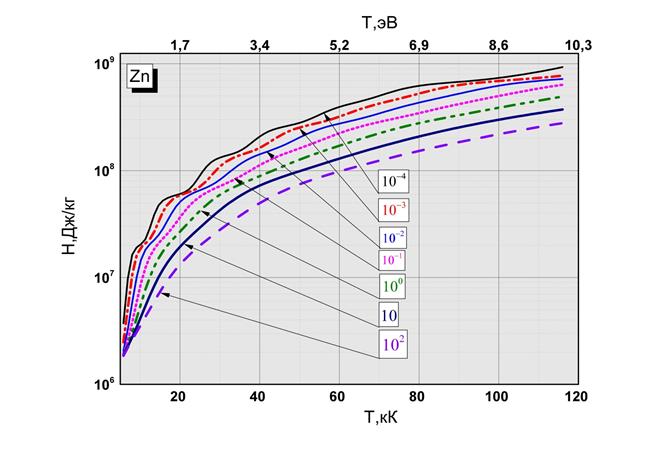Рис.2.4 Зависимость энтальпии от температуры и плотности 
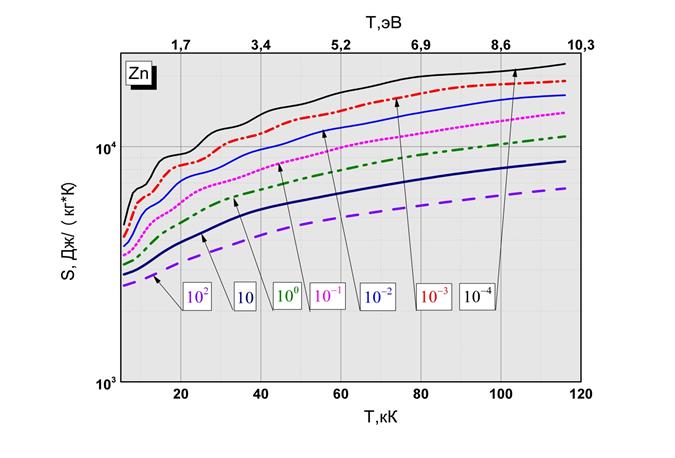Рис.2.5 Зависимость энтропии от температуры и плотности
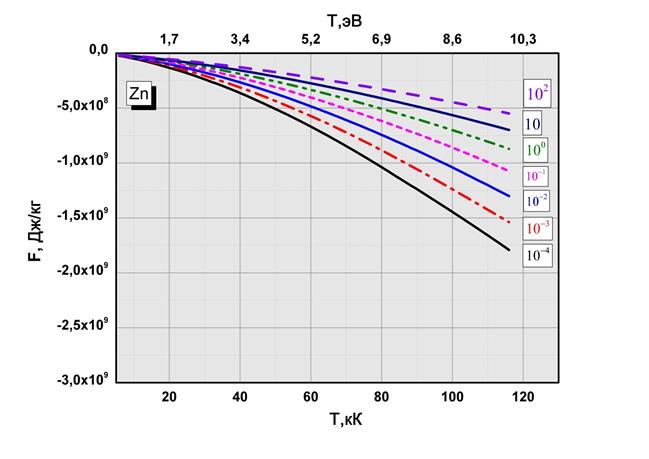Рис.2.6 Свободная энергия в зависимости от температуры и плотности 
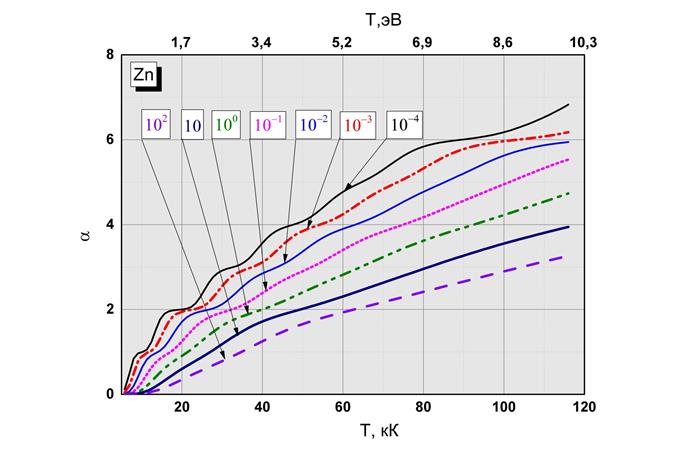Рис.2.7 Степень ионизации в зависимости от температуры и плотности
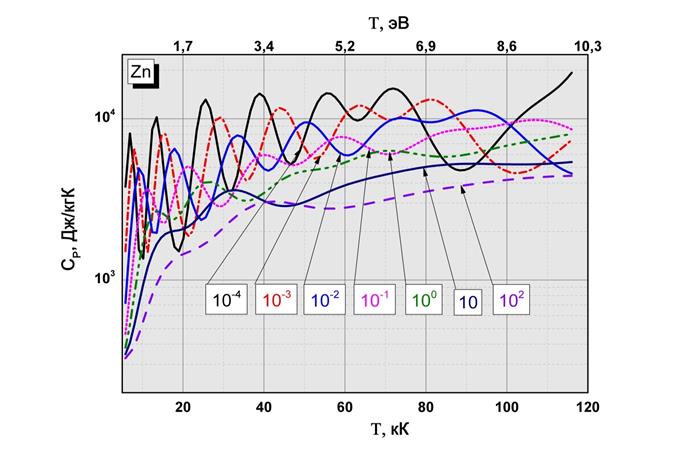
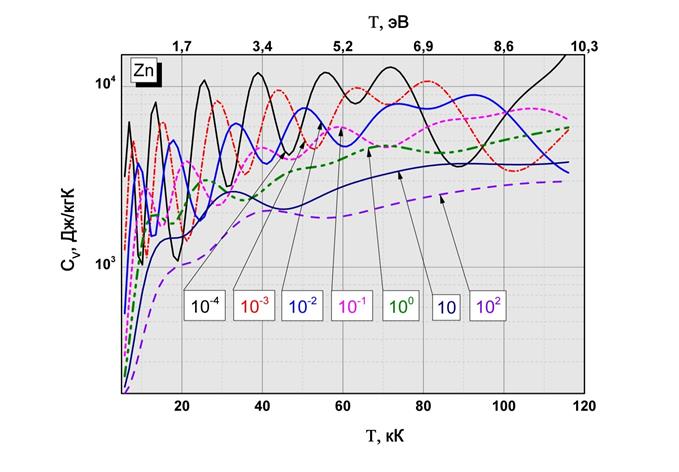Рис.2.8 Зависимости изобарной и изохорной теплоёмкостей от температуры и плотности.
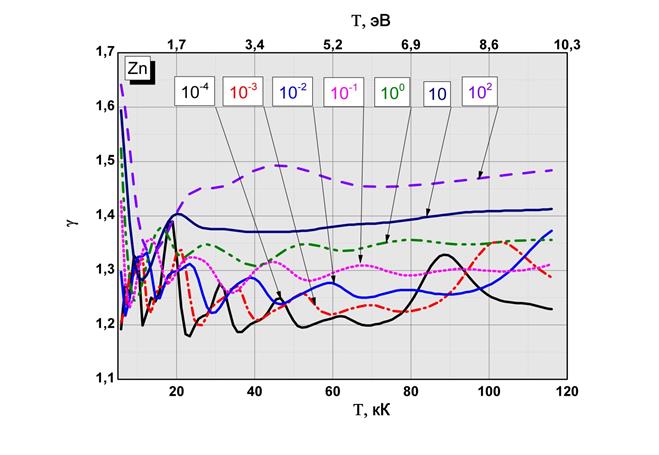
Рис.2.9 Показатель адиабаты в зависимости от температуры и плотности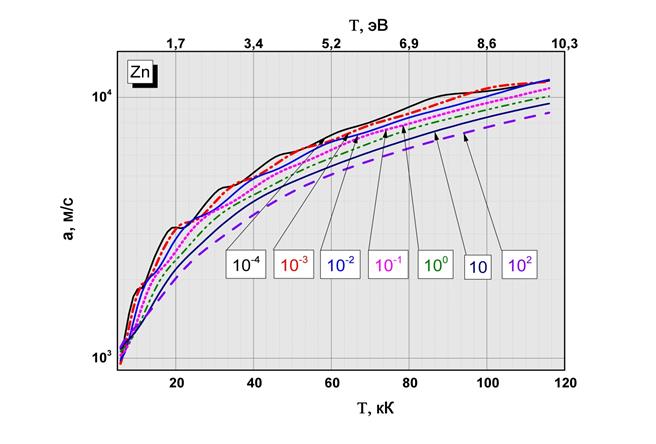 
Рис.2.10 Зависимость адиабатной скорости звука от температуры и плотности
Часть 3