1. Ознакомиться с теоретической частью работы и с описанием измерительной установки.
2. Ознакомиться с «Инструкцией по включению установки и проведению измерений».
3. Включить установку в соответствии с «Инструкцией» и снять следующие характеристики:
– зависимости выходной мощности, генерируемой частоты и анодного тока от анодного напряжения при различных фиксированных напряжениях управляющего электрода (по указанию преподавателя);
– зависимости выходной мощности, генерируемой частоты и анодного тока от напряжения управляющего электрода при различных фиксированных значениях анодного напряжения (по указанию преподавателя).
4. Снять характеристики зависимостей, указанных в п. 3, при работе митрона на рассогласованную нагрузку, а также зависимость нагрузки от анодного напряжения (необходимые изменения в схеме произвести по указанию преподавателя).
5. Провести сравнение характеристик по п. п. 3 и 4.
7.5. Содержание отчета
1. Цель работы.
2. Схематический чертеж митрона с обозначением его основных узлов.
3. Схема измерительной установки и перечень использованных измерительных приборов.
4. Таблицы полученных экспериментальных зависимостей с оценкой точности проведенных измерении и рассчитанных по ним значений КПД.
5. Графики полученных экспериментальных зависимостей в удобном масштабе.
6. Графики расчетных значений зависимости КПД от напряжений на аноде и управляющем электроде.
7. Расчетные значения крутизны электрической перестройки и добротности внешней колебательной системы.
8. Заключение, содержащее объяснение полученных зависимостей.
7.6. Контрольные вопросы
1. В чем заключается характерная особенность процессов энергообмена в скрещенных полях?
2. Каковы конструктивные особенности митрона?
3. Каковы особенности рабочих характеристик митрона?
4. Почему у митрона большой мощности коэффициент перестройки меньше, чем у маломощных митронов?
5. Чем объясняется линейность частотной характеристики митрона?
8. ИССЛЕДОВАНИЕ МАГНИТНЫХ СИСТЕМ ПРИБОРОВ О-ТИПА
Цель работы: ознакомление с конструкцией магнитных систем, обеспечивающих фокусировку электронного пучка в приборах О-типа. Экспериментальное исследование магнитных систем и их компьютерное моделирование.
8.1. Основные теоретические положения
8.1.1. Типы магнитных систем
В приборах О-типа для преобразования энергии источника питания в энергию СВЧ-поля используются электронные пучки, протяженность которых значительно превосходит их поперечные размеры. Для фокусировки (транспортировки) таких пучков в каналах электродинамических систем используются магнитные поля, создаваемые соленоидами или постоянными магнитами [8]. Системы с постоянными магнитами являются более предпочтительными, так как не требуют дополнительного источника питания.
По характеру осевого распределения магнитных полей магнитные системы делятся на три основных типа: системы с однородным полем, системы с реверсивным полем и магнитные периодические системы. Применение реверсивных и периодических полей обеспечивает значительный выигрыш в весе и габаритах магнитных систем.
8.1.2. Магнитная система с однородным полем
Поперечное движение электронов в зоне однородного магнитного поля определяется действием двух сил: силы кулоновского взаимодействия 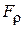 и магнитной фокусирующей силы
и магнитной фокусирующей силы 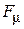 . Первая направлена от оси симметрии системы и оказывает на пучок расфокусирующее действие, вторая, направленная к оси системы, должна противодействовать действие первой. Теоретический анализ дает следующие выражения для указанных сил, действующих на граничные электроны пучка:
. Первая направлена от оси симметрии системы и оказывает на пучок расфокусирующее действие, вторая, направленная к оси системы, должна противодействовать действие первой. Теоретический анализ дает следующие выражения для указанных сил, действующих на граничные электроны пучка:
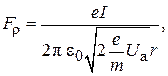 (8.1)
(8.1)
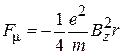 , (8.2)
, (8.2)
где 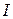 – ток электронного пучка,
– ток электронного пучка, 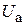 – ускоряющее напряжение,
– ускоряющее напряжение, 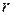 – радиус пучка,
– радиус пучка, 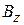 –
– 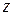 -составляющая магнитной индукции.
-составляющая магнитной индукции.
Уравнение движения граничных электронов пучка в этом случае имеет следующий вид:
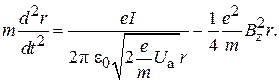 (8.3)
(8.3)
Полагая 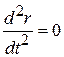 , находим условие баланса расфокусирующей и фокусирующей сил
, находим условие баланса расфокусирующей и фокусирующей сил
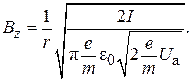
Подстановка в эту формулу численных значений входящих в нее констант дает
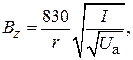 (8.4)
(8.4)
где 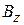 – индукция магнитного поля, выраженная в гауссах,
– индукция магнитного поля, выраженная в гауссах, 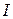 – ток электронного пучка в амперах,
– ток электронного пучка в амперах, 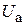 – ускоряющее напряжение в вольтах.
– ускоряющее напряжение в вольтах.
8.1.3. Магнитная периодическая система
Магнитное поле в этом случае является периодической функцией координаты 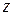 . В большинстве практических случаев осевое распределение магнитного поля с хорошей степенью точности аппроксимируется простым гармоническим законом
. В большинстве практических случаев осевое распределение магнитного поля с хорошей степенью точности аппроксимируется простым гармоническим законом
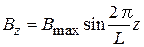 или
или 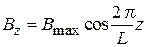 ,
,
где 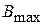 – амплитуда магнитной индукции,
– амплитуда магнитной индукции, 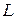 – период магнитного поля.
– период магнитного поля.
Из формулы (8.2) следует, что магнитная сила пропорциональна квадрату магнитной индукции и, следовательно, не зависит от ее знака и оказывается фокусирующей как в положительном, так и в отрицательном полупериодах магнитной индукции. Вместе с тем, так как 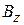 является функцией координаты
является функцией координаты 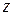 , то в магнитной периодической системе невозможно обеспечить точный баланс кулоновской
, то в магнитной периодической системе невозможно обеспечить точный баланс кулоновской 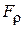 и магнитной
и магнитной 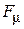 сил на всем протяжении фокусирующей системы. Однако при определенных условиях можно обеспечить баланс этих сил в среднем за период фокусирующей системы. Условие такого баланса может быть записано в виде
сил на всем протяжении фокусирующей системы. Однако при определенных условиях можно обеспечить баланс этих сил в среднем за период фокусирующей системы. Условие такого баланса может быть записано в виде
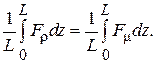 (8.5)
(8.5)
Полагая приближенно, что на отрезке оси 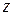 , равном периоду поля
, равном периоду поля 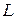 , радиус электронного пуска меняется слабо (
, радиус электронного пуска меняется слабо ( 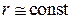 ), c учетом формул (8.1), (8.2), (8.3) получаем
), c учетом формул (8.1), (8.2), (8.3) получаем
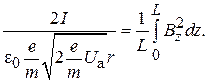 (8.6)
(8.6)
Это соотношение устанавливает связь параметров пучка 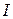 ,
, 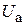 ,
, 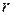 и магнитной индукции
и магнитной индукции 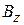 , которая обеспечивает баланс кулоновской и магнитной сил в среднем за период системы.
, которая обеспечивает баланс кулоновской и магнитной сил в среднем за период системы.
Полагая, что 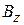 меняется по гармоническому закону, из (8.6) получаем
меняется по гармоническому закону, из (8.6) получаем
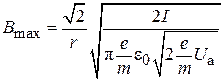 ,
,
или, после подстановки численных значений,
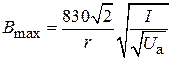 . (8.7)
. (8.7)
Входящие в эту формулу величины имеют те же размерности, что и величины в формуле (8.4). Качественно характер движения электронного пучка в режиме, когда обеспечен баланс кулоновской и фокусирующей сил в среднем за период, может быть описан следующим образом. В области малых значений магнитной индукции пучок расширяется под действием кулоновских сил взаимодействия, однако, попадая в область больших значений магнитной индукции, он испытывает фокусирующее действие магнитной силы и начинает сжиматься. В конце полупериода радиус пучка приближается к его начальному значению. На следующих полупериодах характер движения пучка сохраняется. Периодические изменения радиуса пучка с периодом 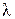 , равным половине периода магнитного поля
, равным половине периода магнитного поля 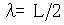 , являются характерной особенностью движения пучка в МПФС. Эти периодические изменения радиуса пучка получили название «волнистости» пучка.
, являются характерной особенностью движения пучка в МПФС. Эти периодические изменения радиуса пучка получили название «волнистости» пучка.
Если условия баланса сил в среднем за период не соблюдены, то движение пучка имеет более сложный характер, к волнистости пучка добавляются пульсации границы пучка, зависящие от соотношения параметров пучка и величины магнитной индукции.
Расчет движения пучка в общем случае требует решения дифференциального уравнения граничной траектории пучка, которое при использовании нормированных (безразмерных) величин может быть представлено в следующем виде [8]:
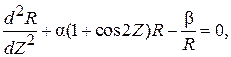 (8.8)
(8.8)
где 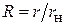 – нормированный радиус пучка;
– нормированный радиус пучка; 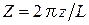 – нормированная продольная координата;
– нормированная продольная координата; 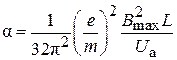 – параметр магнитного поля;
– параметр магнитного поля; 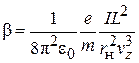 – параметр пространственного заряда,
– параметр пространственного заряда, 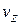 – продольная скорость электронов.
– продольная скорость электронов.
Уравнения (8.3) и (8.8), определяющие движение граничных траекторий электронных пучков в однородном и периодическом магнитных полях не имеют аналитических решений, и расчет траекторий производится на ЭВМ с использованием разработанных для этой цели программ.








