2. Удалить из матриц G (6х8) и D (5х7) столбцы, содержащие нулевой элемент.
3. 
, 
, 
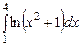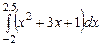, метод трапеций
Вариант 17
1. Найти среднее арифметическое всех элементов между минимальным и максимальным элементами в массивах X (7х8) и Y (34).
2. Отсортировать в порядке возрастания строки матриц N (11х5) и
M (9х7), номера которых задаются пользователем (не менее трех строк).
3. 
, 
, 
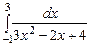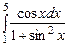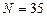, метод трапеций
Вариант 18
1. Отсортировать в порядке убывания столбцы матриц В (9х5) и
А (7х9), номера которых задаются пользователем (не менее трех столбцов).
2. Составить программу вычисления произведения двух квадратных целочисленных матриц А и В размером 15х15.
3. 
, 
, 
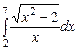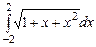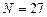, метод Ньютона
Вариант 19
1. Отсортировать в порядке убывания строки матриц N (10х7) и
M (12х11), номера которых задаются пользователем (не менее трех строк).
2. Подсчитать количество элементов матрицы Р (10х12), отличающихся от среднего арифметического значения элементов массива М (100) более чем вдвое, и количество элементов массива М, отличающихся от среднего арифметического значения матрицы Р более, чем втрое.
3. 
, 
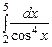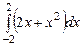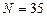, , метод трапеций
Вариант 20
1. Подсчитать количество элементов массива Р (40), отличающихся от среднего арифметического значения элементов матрицы М (6х9) не более чем на два, и количество элементов матрицы М, отличающихся от среднего арифметического значения массива Р не более, чем на три.
2. Составить программу печати в возрастающем порядке всех элементов массива S (100), входящих в него не менее двух раз.
3. 
, 
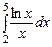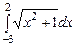, , метод прямоугольников
Вариант 21
1. Удалить из матриц G (10х11) и D (11х10) строки, содержащие нулевой элемент.
2. Отсортировать четные столбцы матрицы А(8х10) в порядке убывания, а нечетные – в порядке возрастания.
3. 
, 
, 
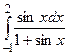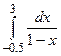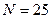, метод прямоугольников
Вариант 22
1. Отсортировать четные строки матрицы Q(10х10) в порядке убывания, а нечетные – в порядке возрастания.
2. Даны матрицы В (m,n) и С (n,m), заполненные случайным образом. Определить, есть ли в заданных матрицах строки, содержащие равное число положительных и отрицательных элементов. Вывести номера строк.
3. 
, 
, 
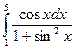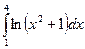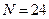, метод Ньютона
Вариант 23
1. Даны матрицы Q (12x9) и С (7x8), заполненные случайным образом. Заменить все элементы первых трех столбцов матрицы Q (12x9) и последних трех столбцов матрицы С (7x8) на их квадраты.
2. Дан целочисленный массив H (50). Вставить в него два элемента: первый – после всех элементов, больших данного числа р, а второй – перед всеми элементами, большими данного числа. Значение р вводится с клавиатуры.
3. 
, 
, 
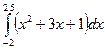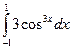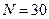, метод парабол
Вариант 24 *
1. Описать рекурсивную логическую функцию, которая проверяет, является ли симметричной часть заданного массива F (40), начинающаяся i-м и кончающаяся j-м элементами.
2. Даны два вектора Y и X размерности n = 30. Вычислить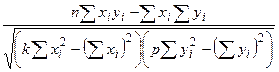 
,
где k – порядковый номер максимального элемента вектора X, а p – порядковый номер максимального элемента вектора Y.
3. 
, 
, 
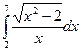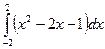, метод трапеций
Вариант 25 *
1. Описать рекурсивную функцию для определения максимального элемента массива W (23), введя вспомогательную рекурсивную функцию, зависящую от k, находящую минимум среди k-последних элементов массива.
2. Даны два вектора Y и X размерности n = 30. Вычислить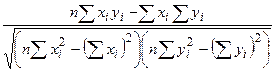 
3. 
, 
, 
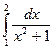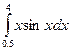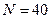, метод прямоугольников
Вариант 26 *
1. В матрице A(m,n), состоящей из нулей и единиц, найти квадрат наибольшего размера (квадратную подматрицу), состоящий целиком из нулей.
2. Клеточное поле размером m*n есть результат игры в крестики-нолики на "бесконечном" поле. Проверить, не закончена ли игра выигрышем "крестиков"? Считается, что "крестики" выиграли, если на поле найдется по горизонтали, вертикали или диагонали цепочка, состоящая подряд из 5 крестиков.
3. , 
, 
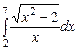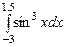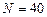, метод парабол
Контрольные вопросы
1. Что такое функция?
2. Что такое функция типа void?
3. Что такое прототип функции?