2. Поменять местами наименьшие из положительных элементов массивов А (55) и В (8х7).

Дата: 2025-05-25; Просмотры: 3

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

3. 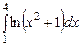, , 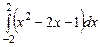, 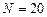метод прямоугольников

Вариант 9

1. В матрицах А (10х15) и В (15х10) заменить все совершенные числа нулями.

2. . Вычислить 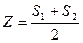, где S₁ – сумма положительных элементов массива X (9х6), а S₂ – сумма отрицательных элементов массива А (60). Суммы вычислять в одной функции.

3. 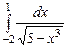, , 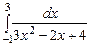, 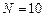метод парабол

Вариант 10

1. Найти сумму наибольших из отрицательных элементов матрицы
А (7х8) и массива В (76).

2. Подсчитать количество элементов массива Р (60), отличающихся от среднего арифметического значения элементов массива М (70) не более чем вдвое, и количество элементов массива М, отличающихся от среднего арифметического значения массива Р не более, чем втрое.

3. 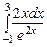, , 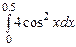, 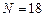метод Ньютона

Вариант 11

1. Поменять местами первый максимальный элемент массива А (60) и последний минимальный элемент массива В (85). Поиск максимального и минимального элементов проводить в одной подпрограмме.

2. Задан массив, состоящий из n неотрицательных элементов. Найти в нем индекс элемента, для которого сумма элементов, стоящих до него, наименее отличается от суммы элементов, стоящих после него.

3. 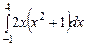, , 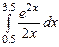, 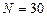метод Ньютона

Вариант 12

1. В матрице A(m,n), состоящей из нулей и единиц, найти квадрат заданного размера (квадратную подматрицу), состоящий целиком из нулей.

2. Даны матрицы В (m,n) и С (n,m), заполненные случайным образом. Определить, есть ли в заданных матрицах столбцы, содержащие по два отрицательных элемента. Вывести номера столбцов.

3. 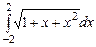, , 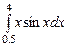, 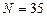метод трапеций

Вариант 13

1. Отсортировать нечетные строки матрицы А(6х7) в порядке убывания, а четные – в порядке возрастания.

2. Найти 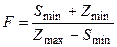, где Z_min и S_min – сумма минимальных элементов матриц Y(9х12) и Q(5х10), а Z_mах и S_mах – разница максимальных элементов заданных матриц.

3. 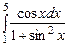, , 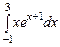, 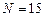метод Ньютона

Вариант 14

1. Поменять местами наибольшие по модулю элементы матрицы А (7х8) и массива В (76).

2. Даны матрицы В (m,n) и С (n,m), заполненные случайным образом. Определить, есть ли в заданных матрицах строки, содержащие по два положительных элемента. Вывести номера строк.

3. 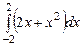, , 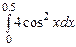, 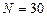метод прямоугольников

Вариант 15

1. Даны матрицы Q (12x9) и С (7x8), заполненные случайным образом. Вставить после столбцов с максимальными элементами столбцы из нулей.

2. Отсортировать нечетные столбцы матрицы А(6х7) в порядке убывания, а четные – в порядке возрастания.

3. 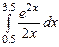, , 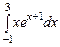, 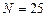метод парабол

Вариант 16

1. Подсчитать общее количество простых чисел среди элементов массивов X (50) и Y (12х5).