2. Что представляет собой имя массива?
3. Что представляет собой индекс элемента массива?
4. Как можно обратиться к элементу массива?
5. Как получить адрес элемента массива?
6. Как описать указатель на начало массива?
7. Как обратиться к элементу массива через указатель?
8. Существует ли связь между индексом элемента и его значением?
9. Чему равен индекс первого элемента массива?
10. Как проинициализировать массив?
11. Когда можно не указывать количество элементов массива при описании?
12. Какого типа могут быть элементы массива?
13. Какие операции можно производить над целым массивом?
14. Почему при обработке массивов используют циклы?
15. Как поменять местами два элемента массива?
16. Чему равен индекс последнего элемента массива?
17. Возникнет ли ошибка при обращении к элементу массива, индекс которого больше индекса последнего элемента этого массива?
18. Может ли существовать массив из одного элемента? Если может, то как его описать?
19. Является ли р указателем на массив а[], если они объявлены следующим образом: int a [10], *p= a ; ?
20. Что такое сортировка массива?
Лабораторная работа № 6. Двумерные массивы
Цель работы – освоить работу с матрицами, научиться правильно организовывать циклы для обработки многомерных массивов.
Постановка задачи
Написать две программы согласно индивидуальному варианту. Использовать обращение к элементам матрицы с помощью операции [] и через указатель. Ввод элементов матрицы осуществлять с клавиатуры. Во время отладки и тестирования программы размер матрицы можно уменьшить. При выводе матрицы следить за тем, чтобы ширина всех столбцов матрицы была одинаковой.
Варианты заданий
Вариант 1
1. Заполнить матрицу А (7х8) нулями и единицами по следующему правилу: если сумма индексов элемента четная, элемент будет нулевым, если нечетная – единичным.
2. Вычислить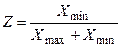 
, где Xmin и Xmax – минимальный положительный и максимальный элементы матрицы
X (6х8).
Вариант 2
1. Вычислить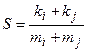 
, где 
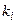и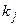 
– индексы строки и столбца минимального положительного элемента, а 
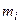и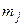 
– индексы строки и столбца первого положительного элемента матрицы Y (5х7).
2. Определить, является ли данная квадратная матрица симметричной относительно своей побочной диагонали.
Вариант 3
1. Заполнить матрицу А (7х8) следующим образом: на главной диагонали – «0», над диагональю – «1», под диагональю – «-1».
2. Поменять местами минимальный элемент матрицы Р (9х11) и элемент, значение которого совпадает с заданным X. Если указанный элемент в матрице отсутствует, вывести сообщение об этом.
Вариант 4
1. Вычислить среднее арифметическое значение элементов, лежащих на диагоналях матрицы В (8х8). Заменить этим значением все элементы матрицы, не лежащие на диагоналях.
2. Подсчитать число элементов матрицы Q (9х11), остаток от деления которых на пять равен единице.
Вариант 5
1. Вычислить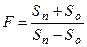 
, где Sn – сумма положительных элементов в нечетных строках матрицы Y(9х12), а So – сумма отрицательных элементов в четных строках той же матрицы.
2. Дана матрица А(10х10). Отсортировать элементы, лежащие на главной диагонали, в порядке возрастания.
Вариант 6
1. Вычислить среднее арифметическое значение элементов, лежащих на диагоналях матрицы С (6х6). Заменить этим значением все диагональные элементы матрицы.
2. Дана матрица размером 7х7. Поменять местами k-й столбец с k-ой строкой (k вводится с клавиатуры).
Вариант 7
1. Отсортировать строки матрицы М (8х5) в порядке возрастания.
2. Вычислить сумму всех элементов матрицы В (10х10), лежащих слева от главной диагонали.
Вариант 8
1. Вычислить сумму элементов матрицы М (9х9), лежащих справа от главной диагонали.
2. Подсчитать число элементов матрицы Q (5х7), кратных трем.
Вариант 9
1. Заполнить матрицу произведениями соответствующих порядковых номеров ее элементов.
2. Найти разность между суммами элементов, лежащих на главной и побочной диагоналях матрицы М (7х7).
Вариант 10
1. Из матрицы Q (6х8) сформировать одномерный массив отрицательных чисел (просмотр по строкам).
2. Определить среднее арифметическое значение элементов матрицы А (8х8), лежащих на главной диагонали.
Вариант 11
1. Дана вещественная матрица М (9х8). Преобразовать матрицу: поэлементно вычесть последнюю строку из всех строк, кроме последней.
2. Дана целочисленная матрица В (7х7). Найти номера столбцов, элементы каждого из которых образуют возрастающую последовательность (b1j<b2j<…<b7j).
Вариант 12
1. Дана вещественная матрица А (8х8). Преобразовать матрицу: поэлементно вычесть последнюю строку из всех столбцов, кроме последнего.
2. В заданной целочисленной матрице размера mxn (m и n – некоторые константы) указать индексы всех элементов, имеющих наибольшее значение.
Вариант 13
1. Транспонированием квадратной матрицы называется такое ее преобразование, при котором строки и столбцы меняются ролями: i-й столбец становится i-й строкой. Дана квадратная матрица размера nxn. Получить транспонированную матрицу.
2. Вычислить сумму элементов матрицы М (9х9), лежащих справа от побочной диагонали.
Вариант 14
1. Дана вещественная матрица D (7х9). Упорядочить (переставить) строки матрицы по возрастанию сумм элементов строк.
2. Сформировать одномерный массив, каждый элемент которого равен количеству отрицательных элементов соответствующего столбца заданной целочисленной матрицы.
Вариант 15
1. Дана вещественная матрица D (7х9). Упорядочить (переставить) строки матрицы по не убыванию наименьших элементов строк.
2. Найти сумму всех элементов матрицы М (9х7) в строках с к1-ой по к2-ую.
Вариант 16
1. Определить, является ли данная квадратная матрица симметричной относительно своей главной диагонали.
2. Найти номера первых отрицательных элементов каждого столбца матрицы D (9х11).
Вариант 17
1. Найти количество элементов в каждой строке матрицы С (8х8), больших среднего арифметического элементов данной строки.
2. Последний отрицательный элемент каждого столбца прямоугольной матрицы заменить нулем.
Вариант 18
1. В каждой строке матрицы В (9х8) сменить знак максимального по модулю элемента на противоположный.
2. В матрице Р (8х9) к элементам столбца к1 прибавить элементы столбца к2. Значения переменных к1 и к2 вводятся с клавиатуры.
Вариант 19
1. В каждой строке матрицы А (7х9) поменять местами первый элемент и максимальный по модулю.
2. Вычислить сумму элементов матрицы Q (10х10), лежащих слева от побочной диагонали.
Вариант 20
1. Поменять местами максимальный и минимальный элементы матрицы А (8х12).
2. Определить, есть ли в матрице Х (8х6) нулевые элементы.
Вариант 21
1. Удалить из матрицы А (12х8) все строки, содержащие единицы.
2. Вычислить среднее арифметическое значение элементов матрицы Р (9х9), лежащих слева от главной диагонали.
Вариант 22
1. Отсортировать строки матрицы А(6х7) в порядке убывания.
2. Подсчитать число элементов матрицы Q (9х6), кратных четырем.
Вариант 23
1. Отсортировать столбцы матрицы А(5х7) в порядке возрастания.
2. Поменять местами максимальный элемент матрицы А (10х12) и элемент, индексы которого вводятся с клавиатуры.
Вариант 24
1. Дана матрица А(9х10). Расставить столбцы таким образом, чтобы элементы в первой строке были упорядочены по возрастанию.
2. Преобразовать матрицу Р (7х7) таким образом, чтобы минимальные элементы строк оказались на побочной диагонали.
Вариант 25
1. Определить седловые точки матрицы М (9х10). Седловая точка – элемент, являющийся одновременно максимальным в своей строке и минимальным в своем столбце.
2. Преобразовать матрицу В (9х9) таким образом, чтобы максимальные элементы строк оказались на главной диагонали.
Вариант 26
1. Дан целочисленный массив В (7х11). Определить, сколько в нем пар соседних одинаковых элементов. Элементы считаются соседними, если их индексы в столбцах и/или в строках различаются не более чем на единицу.
2. Дана матрица А(10х10). Расставить строки таким образом, чтобы элементы в первом столбце были упорядочены по убыванию.
Контрольные вопросы
1. Что такое матрица?