2. Дано натуральное число N. Составить программу для определения количества цифр в этом числе.

Дата: 2025-05-25; Просмотры: 2
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

3. 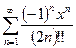, e=10-5,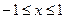

Вариант 5

1. Составить программу поиска двузначных чисел таких, что если к сумме цифр этого числа прибавить квадрат этой суммы, то получится это число.

2. Пусть A и B - положительные вещественные числа, большие 1, причем A>B. Составить программу для поиска такого наименьшего натурального m, что Bm> m*A.

3. 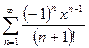, e=10-6,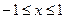

Вариант 6

1. Найти сумму целых положительных чисел из промежутка от А до В, кратных 4. Значения А и В вводятся с клавиатуры.

2. Составить программу для определения, является ли натуральное число k степенью числа 3.

3. 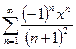, e=10-4,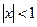

Вариант 7

1. Для натурального числа N получить все его натуральные делители.

2. Дано целое m>1. Получить наибольшее целое k, при котором 4k<m.

3. 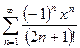, e=0.5*10-5,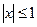

Вариант 8

1. Сумма цифр трехзначного числа кратна 7, само число также делится на 7. Найти все такие числа.

2. Дано натуральное N. Составить программу для поиска первой цифры этого числа.

3. 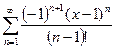, e=10-4,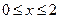

Вариант 9

1. Среди четырехзначных чисел выбрать те, у которых все 4 цифры различны.

2. Дано натуральное число N. Выяснить, является ли оно степенью пятерки.

3. 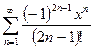, e=10-3,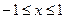

Вариант 10

1. Ввести натуральное число N. Определить, является ли оно совершенным (совершенное число N равно сумме всех своих делителей, не превосходящих само N).

2. Поменять местами цифры старшего и младшего разрядов данного натурального числа (например, из числа 3879 получится 9873).

3. 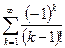, e=0.5*10-5

Вариант 11

1. Ввести натуральные числа А и В. Определить все числа, кратные А и В, меньшие А*В.

2. Найти наименьший общий делитель трех натуральных чисел (1 будет считаться наименьшим общим делителем только в том случае, когда других общих делителей у заданных чисел нет).

3. 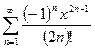, e=0.2*10-5,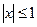

Вариант 12

1. Определить, являются ли натуральные числа А и В взаимно простыми. Взаимно простые числа не имеют общих делителей, кроме единицы.

2. Найти наибольший общий делитель трех натуральных чисел (1 будет считаться наибольшим общим делителем только в том случае, когда других общих делителей у заданных чисел нет).

3. 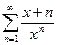, e=10-3,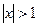

Вариант 13

1. Дано натуральное число N. Вычислить S=1+22+33+…+NN. Формулу возведения в степень не использовать.