3. Отложить на абаке (счетах) число 15. Сколько в этом числе единиц, сколько десятков?
4. Положить монетку в 10 к. (гривенник) и еще 4 к. Сколько всего денег?
5. Взять два десятка палочек. Сколько всего палочек взяли? Отложить число 20 на счетах, на абаке (рис. 7). (Отложить число 20 на абаке и счетах учащиеся должны уметь двумя способами.) В слабых классах целесообразно сначала ознакомить учащихся с устной нумерацией чисел 11 —15, затем показать обозначения этих чисел цифрами, а потом продолжить получение чисел 16— 19, 20 и их обозначение цифрами.
Возможно и одновременное ознакомление учащихся с устной и письменной нумерацией каждого числа второго десятка1.
Изучение письменной нумерации
Незаменимым пособием при изучении письменной нумерации является абак. На абаке учащиеся видят состав числа, место единиц и десятков. Учитывая, что умственно отсталые школьники долго не запоминают место единиц и десятков в числе, меняют их местами, следует писать единицы одним цветом, а десятки — другим, в соответствующие цвета окрашивать и круги абака, обо-
См.: Хилько А. А. Математика: Учебник для 2 класса вспомогательной школы. — М., 1993.
134
значающие десятки и единицы. Нередко можно встретиться и с такими ошибками, когда учащиеся счет разрядов ведут не справа налево, а слева направо, например число 12 записывают как 21. Поэтому на абаке полезно обозначить место единиц цифрой 1, а место десятков цифрой 2 (рис. 8).
Обозначение чисел второго десятка цифрами сопровождается анализом этих чисел. «Число одиннадцать показать на палочках, отложить на абаке. Сколько в этом числе единиц? Сколько в нем десятков? Под единицами поставим цифру 1 синего цвета. Синим цветом будем обозначать единицы. Под десятками поставим цифру 1 красного цвета. Красным цветом будем обозначать десятки. После какого числа в числовом ряду идет число 11? Запишем это число в числовой ряд после числа 10». Таким же образом учитель объясняет запись всех чисел до 19. Каждое число записывается в числовой ряд. Число 20 — это 2 десятка, цифра 0 показывает, что в нем нет отдельных разрядных единиц.
| Рис. 8 |
Наряду с абаком можно использовать любое другое пособие, с помощью которого учитель по-казывает образование чисел второго десятка, а с записью чисел можно знакомить учащихся с помощью таблички с числом 10, замещая нуль различным числом единиц. Таблички с числом 10 сделаны так, что цифра 1 и цифра 0 выдвигаются, а на их место можно поставить другую цифру. «В числе десять, — объясняет учитель, — один десяток, а число единиц равно нулю. В числе тринадцать 1 десяток и 3 единицы. 1 десяток остается, а вместо нуля поставим цифру 3. Это число 13». Цифры, обозначающие единицы и десятки, пишутся двумя цветами (рис. 9).

Рис. 9
Учащиеся должны уметь записывать числа по порядку от 1 до 20, от 11 до 20, записывать их под диктовку учителя, но не по порядку. Надо обязательно обратить внимание учащихся (сами они не смогут заметить этой закономерности), что все числа 11 —19 имеют один десяток на втором месте.
135



 Таблицы чисел от 1 до 20, записанные в два ряда, позволят наглядно сопоставить все числа первого и второго десятка, подме-тить сходство и различие в записи и чтении этих чисел.
Таблицы чисел от 1 до 20, записанные в два ряда, позволят наглядно сопоставить все числа первого и второго десятка, подме-тить сходство и различие в записи и чтении этих чисел.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
Цифры, обозначающие единицы, могут быть записаны одним цветом, а десятки — другим.
На этой же таблице удобно показать, что числа 1—9 записаны одной цифрой — одним знаком, поэтому они называются одно-значными, а числа 11—20 записаны двумя цифрами (знаками), поэтому они называются двузначными. Учитель просит опреде-лить на слух и обозначить двузначное число, а также назвать самое маленькое, самое большое однозначное число, самое ма-ленькое двузначное число, которое они знают. Тем учащимся, которые смешивают место десятков и единиц в числе, необходимо разрешить эти числа записывать и в тетради цветными карандашами или шариковой ручкой в два цвета, а на доске писать их цветными мелками.
Продолжая работу над нумерацией, следует проводить упраж-нения на установление соотношения между предметным множест-вом, числом и его обозначением цифрами. Например, учитель вызывает к доске несколько учеников и дает задание показать число 15: одному — на палочках, другому — на абаке, третьему — на счетах, четвертому — на линейке, пятому — записать на доске, шестому — найти в числовом ряду.
Проводится сравнение чисел. Учащиеся должны усвоить правило: все числа, стоящие в числовом ряду слева от данного числа, меньше его, а все числа, стоящие в числовом ряду справа от данного числа, больше его.
Сравниваются числа второго десятка: определяется, какое число больше (меньше), сколько лишних единиц в большем числе и сколько их недостает в меньшем числе.
Отношения между числами записываются знаками > (больше), < (меньше), = (равно), которые усваивают учащиеся 2-го класса. Необходимы задания, в которых бы учащиеся могли правильно расставить знаки соотношения >, <, =. Например: «Вставь между числами 7 ... 17, 14 ... 12, 11 ... 11 нужный знак >, <, = ».
Для закрепления знаний о месте числа в натуральном ряду чисел проводятся упражнения на нахождение пропущенных чисел
136
и нахождение соседних чисел, запись чисел по порядку от мень-шего к большему или от большего к меньшему, определение наи-большего однозначного числа и наименьшего однозначного и дву-значного чисел и т. д.
На протяжении работы над вторым десятком необходимо за-креплять навыки сознательного счета. Счет ведется не только от 1, но и от любого заданного числа («Считай от 7 до 20. Считай от 9 до 19. Считай обратно от 20 до 10, от 18 до 6»). Учащиеся учатся присчитывать и отсчитывать не только по 1, но и по 2, 3, 4,5, сначала опираясь на группы предметов, числовые фигуры, а потом и без опоры на них.
Большое внимание, как и при изучении чисел первого десятка, уделяется порядковому счету. Учащиеся должны уметь отвечать на вопросы: «В котором ряду ты сидишь? В котором ряду слева стоит Миша? Пересчитайте по порядку».
После того как учащиеся научились обозначать числа второго десятка цифрами, надо продолжить работу над анализом чисел по десятичному составу не только на пособиях, но и без них. Дву-значные числа раскладываются на десятки и единицы и составляются из десятков и единиц: 13=1 дес. 3 ед.; 1 дес. 3 ед. = 13; 13=10+3; 10+3=13.
Полезны и такие задания: «Какое число получится, если из числа 15 вычесть все единицы, 1 десяток?»
В связи с изучением нумерации вводятся примеры на сложение и вычитание, решение которых основано и на знании свойств натурального ряда чисел (12 + 1, 14—1), и на знании десятичного состава чисел (10+5, 5+10, 15-5, 15-10).
Полезно при решении примеров сопоставить операции над числами первого и второго десятка:
2+1= 3 3-1= 2
12+1 = 13 13-1 = 12
Сложение и вычитание в пределах 20
Овладение вычислительными приемами сложения и вычитания в пределах 20 основано на хорошем знании сложения и вычитания в пределах 10, знании нумерации и состава чисел в пределах 20.
При изучении действий сложения и вычитания в пределах 20, как и при изучении соответствующих действий в пределах 10, большое значение имеют наглядность и практическая деятель-
137


 ность с пособиями самих учащихся. Поэтому все виды наглядных пособий, используемых при изучении нумерации, найдут примене-ние и при изучении арифметических действий.
ность с пособиями самих учащихся. Поэтому все виды наглядных пособий, используемых при изучении нумерации, найдут примене-ние и при изучении арифметических действий.
Однако по сравнению с изучением действий в пределах 10 большое внимание уделяется использованию условно-предметных пособий: брусков и кубиков арифметического ящика, абаков, счетов.
Действия сложения и вычитания целесообразно изучать парал-лельно — после знакомства с определенным случаем сложения изучать соответствующий случай вычитания в сопоставлении со сложением, например: 10+7, 7+10, 17— 7 и 17—10. Учитель должен постоянно обращать внимание на взаимосвязь этих дейст-вий.
Во 2-м классе учащиеся должны знать название компонентов действий сложения и вычитания:
| 10 | + | 7 | = | 17 |
| 1-е слагаемое | 2-е слагаемое | сумма |
| 17 | — | 7 | = | 10 |
| уменьшаемое | вычитаемое | разность |
Покажем последовательность и приемы изучения сложения и вычитания в пределах 20.
I. Приемы сложения и вычитания, основан-
ные на знаниях десятичного состава числа
(10+3, 13—3, 13—10) и нумерации чисел в пределах
20 (16+1, 17-1).
При решении этих примеров закрепляются взаимосвязь сложе-ния и вычитания, переместительное свойство сложения, названия компонентов и результатов действий. При этом учащиеся постепенно перестают пользоваться наглядными пособиями, но от них требуется пояснение действий.
II. Сложение и вычитание без перехода через
десяток.
Выполнение действий основано на разложении компонентов на десятки и единицы:
138
а) к двузначному числу прибавляется однозначное. Из дву-значного числа вычитается однозначное.
Сначала нужно рассмотреть случаи, когда количество единиц в двузначном числе больше, чем во втором слагаемом (13+2, 14+3), и только потом включать случаи вида 11+6, 13+5, хотя приемы их решения одинаковы.
Объяснение сопровождается использованием наглядных посо-бий и подробной записью решения, например: 13+2. Первое сла-гаемое (13) состоит из 1 десятка и 3 единиц: 1 десяток палочек и еще 3 палочки. Второе слагаемое 2. Прибавляем 2 палочки. 3 палочки и 2 палочки — 5 палочек и 1 десяток палочек. Получи-лось 1 десяток (палочек) и 5 единиц (палочек) — это число 15. Значит, 13+2=15. Подобным образом объясняются и случаи вычитания.
Важно постоянно подчеркивать, что складываются и вычитают-
ся при решении таких примеров единицы. При записи примера
учащиеся могут подчеркивать единицы: 14+2 = 16, 16—2 = 14.
Иногда целесообразно единицы и десятки записывать разным цве-
том. На доске их можно обводить кружочком.
При решении примеров на сложение закрепляется умение учащихся пользоваться переместительным законом сложения: решение примера 2+14 проводится на основе решения примера 14+2. Полезно сопоставлять примеры на сложение и вычитание в пределах 20 с примерами на те же действия в пределах 10:
7+ 2= 9 9-2= 7 5+ 3= 8- 3=
2+ 7= 9 9-7= 2 3+...= 8-...=
17+ 2=19 19-2=17 17+ 2= 19- 2=
2+17=19 19-7=12 2+...= 19-...=
б) получение суммы 20 и вычитание однозначного числа из 20:
15+5 17+3 20-5 20-3
Решение примеров такого вида, особенно на вычитание, вызы-вает значительные трудности у многих умственно отсталых школьников. Учащихся смущает то, что при сложении единиц в разряде единиц получается нуль. Разложив 20 на два десятка и вычтя из одного десятка заданное количество единиц, дети забывают этот результат прибавить к десятку и получают ошибочный ответ: 20—3=7.
Использование наглядных пособий, актуализация имеющихся знаний и опора на них помогают преодолеть эти трудности. Необ-
139
ходимо повторить таблицу сложения и вычитания в пределах 10, дополнение однозначного числа до десятка, вычитание из 10.
Объяснение сложения не представляет ничего нового по сравне-нию с объяснением решения примеров вида 13+2, кроме образова-ния 1 десятка: 5+5=10 (или 1 дес); 1 дес + 1 дес.=2 дес.=20.
Рассмотрим пример на вычитание: 20—3. В числе 20 нуль единиц, а нужно вычесть 3 единицы. Занимаем 1 десяток, раздроб-ляем его на 10 единиц и вычитаем 3 единицы, получаем 7 единиц. Всего остается 1 десяток и 7 единиц, или 17. Проведенное рассуж-
|
|
дение записывается так: 20—3 = 17.
В случае затруднений при понимании и приема вычислений объяснение можно провести с помощью палочек, связанных в пучки. Например, 20 — это 2 десятка (берем 2 пучка палочек) и нуль единиц. Занимаем 1 десяток и раздробляем его на 10 единиц (развязываем пучок палочек). 10 единиц минус 3 единицы получа-ется 7 единиц. Всего остается 1 десяток и 7 единиц, или 17.
Решаются примеры на перестановку слагаемых, составляются по образцу, по аналогии:
17+ 3 14+6 11+ 9=20 12+8 20-7
3+17 6+[ ] [ ]+[ ]=20 20-8 13+7
Действия сложения и вычитания сопоставляются: 15+5=20; 20-5=15;
в) вычитание из двузначного числа двузначного: 15—12; 20—15 Решение примеров такого вида можно объяснить разными приемами:
1) разложить уменьшаемое и вычитаемое на десятки и единицы и вычитать десятки из десятков, единицы из единиц;
2) разложить вычитаемое на десяток и единицы. Вычитать из уменьшаемого десятки, а из полученного числа — единицы.
Учащимся трудно знакомиться сразу с двумя приемами и даже трудно последовательно знакомиться сначала с одним, а потом с другим приемом. Умственно отсталые школьники самостоятельно не могут выбрать, когда целесообразнее использовать тот или иной прием. Поэтому знакомство с двумя приемами только запутывает их. Лучше отработать хорошо один прием вычислений и научить учащихся самостоятельно пользоваться им.
Объяснение вычитания проводится на наглядных пособиях.
Например, 15—12. «Какое действие надо выполнить? Прочитайте пример. Назовите уменьшаемое, вычитаемое. Сколько знаков имеют эти числа? Как они называются? Сегодня будем учить-
ся вычитать из двузначного числа двузначное. Из чего состоит число 15? Отложим его на счетах. Из чего состоит вычитаемое 12? Вычитать будем так: от 15 отнимем 1 десяток. Какое число осталось? От 5 единиц отнимем 2 единицы. Какое число получи-лось в остатке? Значит, 15—12=3».
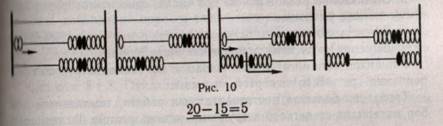
Аналогично объясняется вычитание двузначного числа из 20 (рис. 10). Покажем на счетах последовательность вычитания дву-значного числа из 20:
Далее следует сопоставить решение примеров вида:
| 20- 3= 20-13= |
| 15+2= 17 -2= |
17+ 3 = 3+17 =
Целесообразно также использовать прием составления одного примера на сложение с тремя примерами: одного на сложение (перестановка слагаемых) и двух на вычитание. Необходимо сопо-ставлять компоненты этих примеров, подчеркивать их взаимосвязь (12+5, 5+12, 17-5, 17-12).
III. Сложение и вычитание с переходом через разряд представляет наибольшие трудности для учащихся школы VIII вида. Трудности связаны с тем, что сразу происходит актуализация ранее полученных знаний, их упорядочение и последовательное выполнение ряда логических операций. Чтобы сложить числа 7 и 5, нужно выполнить следующие операции:
1. Разложить второе слагаемое (5) на два числа так, чтобы одно из них дополняло первое слагаемое до 10.
2. Дополнить первое слагаемое до 10, т. е. прибавить к первому слагаемому (7) одно из чисел, на которое разложили второе слагаемое (т.е. 3).
3. К полученному числу (10) прибавить оставшееся число (2).
Учащиеся затрудняются, во-первых, в разложении второго слагаемого, так как, чтобы его разложить, нужно произвести мыслен-



 но две операции: а) определить, сколько единиц недостает в пер-вом слагаемом до десятка; б) разложить второе слагаемое.
но две операции: а) определить, сколько единиц недостает в пер-вом слагаемом до десятка; б) разложить второе слагаемое.
Вторая трудность заключается в том, чтобы удержать в памяти число, которое осталось после дополнения первого слагаемого до десятка, например: 7+5. Учащиеся дополнили 7 до 10, но не помнят, сколько же нужно прибавить к 10.
Вычитание с переходом через десяток (12—5) тоже требует ряда операций:
1. Уменьшаемое разложить на десяток и единицы.