Функцию F( x) называют интегральной функцией распределения или интегральным законом распределения.
9. Непрерывные случайные величины. Интегральный и дифференциальный законы распределения непрерывной случайной величины. Свойства функции и плотности распределения.
Случайной называют величину, которая в результате испытания пример одно и только одно возможное значение, наперед не известное и зависящее от случайных причин, которые заранее не могут быть учтены.
Например, если случайная величина Х имеет три возможных значения, то они будут обозначены так: х1, х2, х3
 |
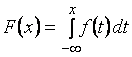Более строго случайная величина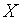 
называется непрерывной, если существует неотрицательная функция 
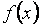, удовлетворяющая следующему равенству при любых 
:
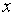где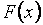 
– функция распределения случайной величины Х, т. е. 
.
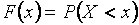Непосредственно из определения интегральной функции распределения вытекают следующие свойства F ( x ):
1. 
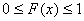. Это следует из того, что F(x)=P(X<x), а вероятность P – есть число заключённое между нулём и единицей.
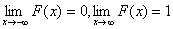Легко видеть, что
Дифференциальной функцией распределения или функцией плотности вероятности называется первая производная от интегральной функции распределения, т.е.F’(x)=f(x). Из этого определения видно, что функция плотности вероятности существует только для непрерывных случайных величин.
Пусть случайная величина X задана функцией плотности вероятности f(x). Вероятность того, что эта случайная величина примет значения, принадлежащие интервалу [a,b] равна определенному интегралу от дифференциальной функции распределения в пределах от a до b
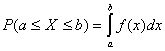
Это следует из того, что
P(a<X<b)=F(b)-F(a)
а по формуле Ньютона-Лейбница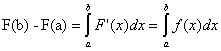 
Функцию F( x) называют интегральной функцией распределения или интегральным законом распределения.
Способ задания непрерывной случайной величины с помощью функции распределения не является единственным. Необходимо определить некоторую функцию, отражающую вероятности попадания случайной точки в различные участки области возможных значений непрерывной случайной величины. Т. е. представить некоторую замену вероятностям pi для дискретной случайной величины в непрерывном случае.
Такой функцией является плотность распределения вероятностей. Плотностью вероятности (плотностью распределения, дифференциальной функцией) случайной величины Х называется функция f( x), являющаяся первой производной интегральной функции распределения:
.
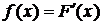10. Числовые характеристики непрерывной случайной величины: математическое ожидание, дисперсия, коэффициенты асимметрии и эксцесса.
Математическое ожидание. Математическим ожиданием дискретной случайной величины Х , принимающей конечное число значений хi с вероятностями рi , называется сумма:
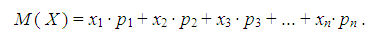
Математическим ожиданием непрерывной случайной величины Х называется интеграл от произведения ее значений х на плотность распределения вероятностей f(x):
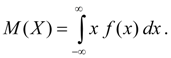
Свойства математического ожидания: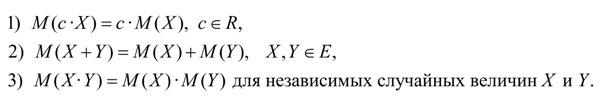 
Определение. Дисперсией непрерывной случайной величины называется математическое ожидание квадрата ее отклонения.
Дисперсия. Дисперсией случайной величины Х называется число:
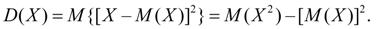(8)
Дисперсия является характеристикой рассеяния значений случайной величины Х относительно ее среднего значения М ( Х ). Размерность дисперсии равна размерности случайной величины в квадрате. Исходя из определений дисперсии (8) и математического ожидания (5) для дискретной случайной величины и (6) для непрерывной случайной величины получим аналогичные выражения для дисперсии:
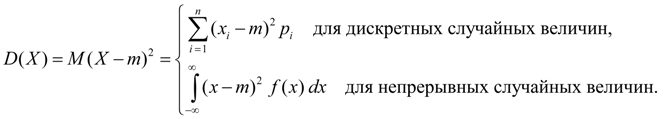
Здесь m = М ( Х ).
Свойства дисперсии:
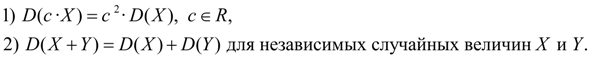Определение. Отношение центрального момента третьего порядка к среднему квадратическому отклонению в третьей степени называется коэффициентом асимметрии.
Центральный момент третьего порядка:
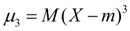(17)
служит для оценки асимметрии распределения. Если распределение симметрично относительно точки х = m, то центральный момент третьего порядка будет равен нулю (как и все центральные моменты нечетных порядков). Поэтому, если центральный момент третьего порядка отличен от нуля, то распределение не может быть симметричным. Величину асимметрии оценивают с помощью безразмерного коэффициента асимметрии:
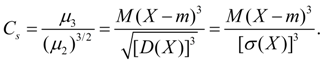(18)
Знак коэффициента асимметрии (18) указывает на правостороннюю или левостороннюю асимметрию (рис. 2).
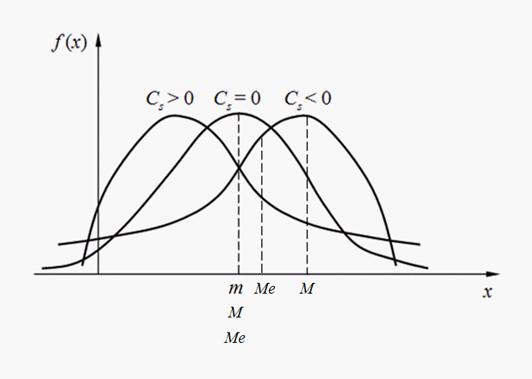
Определение. Для характеристики островершинности и плосковершинности распределения используется величина, называемая эксцессом.
Эксцесс. Центральный момент четвертого порядка:
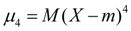(19)
служит для оценки так называемого эксцесса, определяющего степень крутости (островершинности) кривой распределения вблизи центра распределения по отношению к кривой нормального распределения. Так как для нормального распределения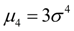 
, то в качестве эксцесса принимается величина:
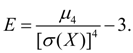(20)
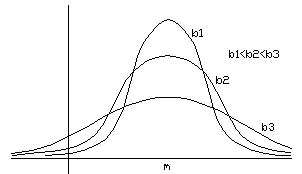
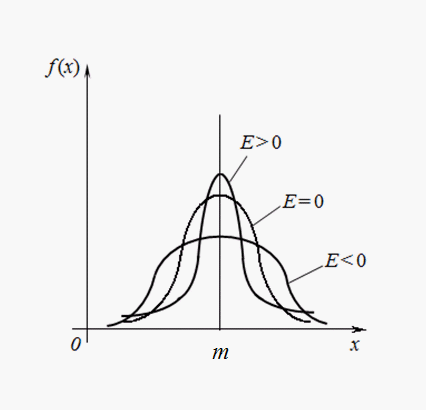
На рис. 3 приведены примеры кривых распределения с различными значениями эксцесса. Для нормального распределения Е = 0. Кривые, более островершинные, чем нормальная, имеют положительный эксцесс, более плосковершинные – отрицательный.
11. Законы распределения: показательный, нормальный, экспоненциальный. Графики, параметры распределений.
Непрерывная случайная величина Х имеет показательный(экспоненциальный) закон распределения с параметром λ, если ее плотность вероятности имеет вид
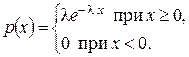
Функция распределения случайной величины, распределенной по показательному закону, равна
 |
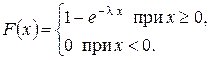
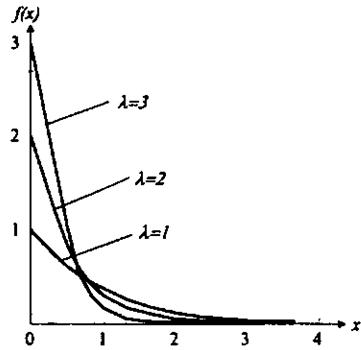График функции плотности вероятности f(x) (кривая распределения) показательного закона в зависимости от величины параметра λ показан на рис
Нормальный закон распределения имеет плотность распределения
(*)
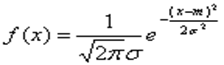где m и s>0 некоторые числовые параметры. В разделе «Предельные теоремы теории вероятностей.» будут обсуждены причины, в силу которых нормальный закон распределения играет важную
роль в теории вероятностей и ее приложениях.
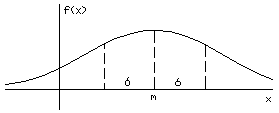
х. Легко убедиться, что кривая, определяемая функцией распределения (*), имеет максимум в точке x=m, а точки перегиба отстоят от точки x=m на расстоянии s и при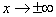 
функция (*) асимптотически приближается к нулю.
