Вопрос 18. числовые характеристики системы двух случайных величин. Начальные, центральные моменты.
· Начальным смешанным моментом порядка(i,k),двумерной случайной величины (х1,х2)называется число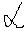 
i,k следовательно 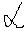i,k=M[x1i;x2j]
Найти начальный смешанный момент порядка (1;0)
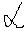1,0=М[x11;x20]=M[x1]
· Центральным смешанным моментом порядка (i,k)случайной велечены (х1;х2) называется число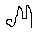 
i,k =М[([1-mx1)i*(x2- mx2)K]
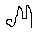2,0= М[([1-mx1)2*(x2- mx2)0]=D[x1]
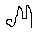0,2= М[([1-mx1)0*(x2- mx2)2]=D[x2]
Особую роль имеет центральный смешанный момент порядка (1;1)
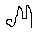1,1= М[([1-mx1)1*(x2- mx2)1]= математическое ожидание произведения центрированных величин х и у.
1,1-называет ковариацией и обозначают cou(x1;x2).
19. Корреляционный момент. Коэффициент корреляции.
Чтобы привести ковариация (cov) к линейным единицам измерения, нормируют cov
Коэффициент корреляции
Корреляция, это степень зависимости между двумя случайными величинами X и Y. Для исследования подобных зависимостей пользуются конечным (выборочным) набором пар значений (x1 , y1) , (x2 , y2) ,…, (xn , yn)
где xk — k-е значение случайной величины Х, а yk — соответствующее ему значение случайной величины Y.
Корреляция - величина, отражающая наличие связи между явлениями, процессами и характеризующими их показателями.
Корреляционная зависимость - определение зависимости средней величины одного признака от изменения значения другого признака.
Коэффициент корреляции величин х и у (rxy) свидетельствует о наличии или отсутствии линейной связи между переменными:
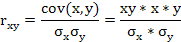
где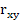 
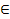(-1; 1). Если: 
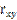= -1, то наблюдается строгая отрицательная связь; 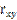= 1, то наблюдается строгая положительная связь; 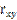= 0, то линейная связь отсутствует.
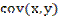- ковариация, т. е. среднее произведение отклонений признаков от их средних квадратических отклонений.
Коэффициент корреляции может служить мерой зависимости случайных величин.
20. Уравнение линейной регрессии. Коэффициент линейной регрессии.
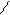Вероятность зависимости означает, что с изменением с.в. Х, с.в. Y имеет тенденцию также изменяться.
Уравнение линеной регрессии Y на Х – уравнение Y= ax+b, параметры которого минимизируют остаточную дисперсии.
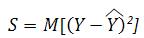
S(a,b)=M[(Y-(ax+b)2]®mina,b
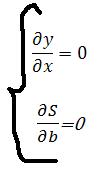Точка является решением этой системы, будет доставлять минимум S(a,b)
Коэффициенты линейной регрессии.
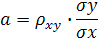
b =- amx + my
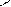Подставим коэффициенты в уравнение линеной регрессии
Y-mx = rxy*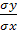 
(x-mx)
Вопрос 21.
Если СВ зависимы м/у собой то для характеристики их зависимости вводиться понятие условного закона распределения.
Условный закон распределения одной из СВ входящих в систему ХУ называется ее закон распределения найденный при условии что другая СВ принела определенное значение.
Условная плотность, условное мат.ожидание обладает всеми св-ми плотности и мат.ожидания.
Вопрос 22.
Ранее было приведено понятие линейной регрессии, более общее понятие когда нет основания предполагать наличие линейной зависимости.
Регрессией ХУ- называется условное мат.ожидание.
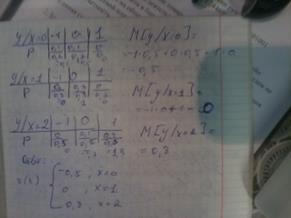
Пример:
