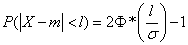Вероятность попадания случайной величины на заданном участке.
1вопрос.
· Событие- это факт который в результате опыта может произойти или нет.
· Непосредственные исходы событий называются элементарные события и обозначаются W.
· События называются достоверными, если оно обязательно наступит.
· Событие называется невозможным, если оно заведомо не произойдет.
· Два события называются - не совместны, если появление одного из них исключает появление другого в одном опыте.
Событие образует полную группу событий, если они попарно не совместны, и в результате опыта происходит одно и только из них.
Ø Классическая схема вычисления вероятности:
Происходит опыт с n- исходами, которые можно представить в виде полной группы событий не совместных равновозможных событий.
Такие исходы называются случайными элементарными событиями.
Случай W который приведет к наступлению к А называется благоприятным событию А.
Вероятность события А называется число m-благоприятных событию А к общему числу n.
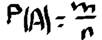
Из классической ОП! вероятности следует 0<=P<=1
0-невозможно
1-достоверность
2вопрос.
· Относительной частотой события А (Р*(А)) в серии n опытах называется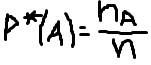 
0<=P*(A)<=1
· Статистической вероятностью события А называется число около которого калеблица относительная частота события А при достаточном большом числе испытаний.
Р*(А)приблизительна равна Р(А).
3. Действия над событиями. Сложение событий. Сложные события.
Событие – факт, который в результате опыта может произойти или не произойти.
Сумма (объединение) событий представляет собой сложное событие, состоящее в появлении хотя бы одного из событий А и В. Объединение событий обозначается как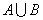 
, или 
.
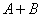Событие C произведением A и B, если оно состоит из всех элементарных событий, входящих и в A, и в B.
Разностью событий A-B называется событие C, состоящее из всех элементарных событий, входящих в A, но не входящих в B.
События A и B называются несовместными, если они никогда не могут произойти в результате одного испытания.
Противоположным событием А, называется событие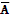 
, которое происходит, когда не происходит А
4. Теорема сложения вероятностей. Следствия.
Теорема (сложения вероятностей). Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий.
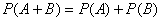
Говорят, что несколько событий в данном опыте образуют полную группу событий, если в результате опыта непременно должно появиться хотя бы одно из них.
Следствие 1: Если события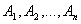 
образуют полную группу несовместных событий, то сумма их вероятностей равна единице.
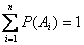
Определение. Противоположными называются два несовместных события, образующие полную группу.
Следствие 2: Сумма вероятностей противоположных событий равна единице.
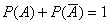
Вопрос 5.
· Условной вероятностью события В при условии что произошло событие А называется отношение произведение события к вероятности события А.
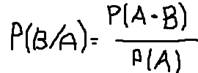
· Теорема умножения вероятности:
Р(А*В)=Р(В/А)*Р(А)=Р(А/В)*Р(В)
вероятность двух событий равна произведению условной вероятности одного из них на безусловную вероятность другого.
Р(А*В*С)=Р(В/А)*Р(А)*Р(С/АВ)
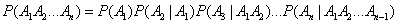
· Событие А и В называются независимыми если Р(А*В)=Р(А)*Р(В)
· Событие А независимо от В если его условная вероятность равна безусловной.
Р(ф/В)=Р(А).
Вопрос 6.Формула полной вероятности:
Теорема:
Пусть событие а может произойти с одним из событий H1,H2…Hn, образующих полную группу событий называемых гипотезой.
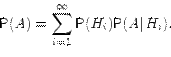
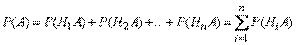см лекцию
7. Формула Байеса
Имеется событие А которое может произойти с одной из гипотез Н1,Н2…Нn которые образуют полную группу событий
Событие А произошло
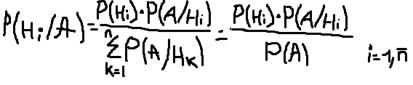
Пример. В магазин поступила новая продукция с трех предприятий. Процентный состав этой продукции следующий: 20% - продукция первого предприятия, 30% - продукция второго предприятия, 50% - продукция третьего предприятия; далее, 10% продукции первого предприятия высшего сорта, на втором предприятии - 5% и на третьем - 20% продукции высшего сорта. Найти вероятность того, что случайно купленная новая продукция окажется высшего сорта.
Решение. Обозначим через В событие, заключающееся в том, что будет куплена продукция высшего сорта, через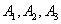 
обозначим события, заключающиеся в покупке продукции, принадлежащей соответственно первому, второму и третьему предприятиям.
Можно применить формулу полной вероятности, причем в наших обозначениях:
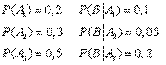
Подставляя эти значения в формулу полной вероятности, получим искомую вероятность:
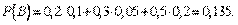
8. Повторные опыты. Формула Бернулли. Теорема Муавра-Лапласа
Испытания или опыты называют независимыми, если вероятность каждого исхода не зависит от того, какие исходы имели другие опыты, т.е. вероятность каждого исхода остается постоянной от опыта к опыту.
Пусть, в общем случае, производится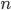 
независимых испытаний. Ставится задача определения вероятности того, что ровно в 
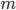испытаниях наступит событие 
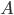, если вероятность наступления этого события в каждом испытании равна 
.
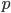Определим вначале вероятность того, что в первых 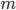испытаниях событие 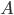наступит, а в остальных 
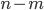испытаниях — не наступит. Вероятность такого события может быть получена на основании формулы вероятности произведения независимых событий
,
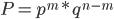где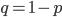 
.
Так как рассматривалась только одна из возможных комбинаций, когда событие 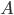произошло только в первых 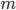испытаниях, то для определения искомой вероятности нужно перебрать все возможные комбинации. Их число будет равно числу сочетаний из 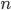элементов по 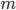, т.е. 
.
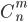Таким образом, вероятность того, что событие 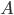наступит ровно в 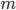испытаниях определяется по формуле
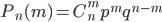, (3.3)
где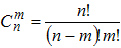 
.
Формула (3.3) носит название формулы Бернулли.
Пример. В четырех попытках разыгрываются некоторые предметы. Вероятность выигрыша в каждой попытке известна и равна 0,5. Какова вероятность выигрыша ровно трех предметов?
Решение. По формуле Бернулли находим
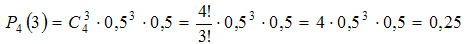
Пусть в каждом из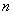 
независимых испытаний событие A может произойти с вероятностью 
, 
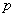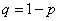(условия схемы Бернулли). Обозначим как и раньше, через 
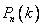вероятность ровно 
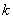появлений события А в 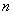испытаниях. кроме того, пусть 
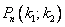– вероятность того, что число появлений события А находится между 
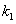и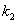 
.
Локальная теорема Лапласа.
Если n – велико, а р – отлично от 0 и 1, то
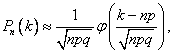где 
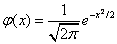- функция Гаусса (функция табулирована, таблицу можно скачать на странице формул по теории вероятностей).
Интегральная теорема Лапласа.
Если n – велико, а р – отлично от 0 и 1, то
P(n; k1, k2)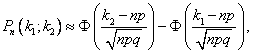 
где 
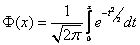- функция Лапласа (функция табулирована, таблицу можно скачать на странице формул по теории вероятностей).
Функции Гаусса и Лапласа обладают свойствами, которые необходимо знать при использовании таблиц значений этих функций:
а) 
б) при больших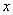 
верно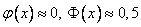 
.
Пример. Для мастера определенной квалификации вероятность изготовить деталь отличного качества равна 0,75. За смену он изготовил 400 деталей. Найти вероятность того, что в их числе 280 деталей отличного качества.
Решение. По условию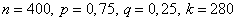 
, откуда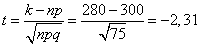 
По таблицам найдем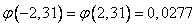 
.
Искомая вероятность равна: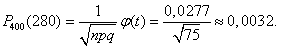 
Вопрос 9.
· Случайная величина –это величина, которая в результате опыта принимает то или иное значение ,при чем не известно заранее какое именно.
· С.В х имеет дискретное распределение если сущ.конечное или счетный набор чисел таких что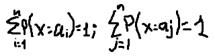 
закон дискрет.распределения:
Дискретное распределение удобно задавать таблицей:
| Х | а1 | а2 | … | an |
| Р | Р1 | Р2 | … | Pn |
Рi= P(x=ai), i=1,n сумма вероятностей =1.
Случ.вел. х имеет непрерывное распределение если существует неотрицательная функция f(x), такая что для любого промежутка (а,в) числовой прямой
Р(х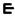 
(а,в))=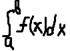 
f(x)-плотность распределения.
Она должна удовлетворять:
1.f(x)>=0
2. 
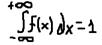
Вопрос 10.
Функцией распределения случайной величины Х называют функцию F(x), определяющую для каждого значения х, вероятность того, что случайная величина Х примет значение меньше х, т.е.
F(x) = P (X <x).
Функция распределения обладает следующими свойствами:
1. Значение функции распределения принадлежит отрезку [0,1]: 0 ≤ F(x) ≤ 1.
2. Функции распределения есть неубывающая функция, х1<x2.F(x1)<=F(x2).
3. Вероятность того, что случайная величина Х примет значение, заключенное в интервале (а, b), равна приращению функции распределения на этом интервале:
Р(а < X < b) = F(b) – F(а). (2.1)
4. Если все возможные значения случайной величины Х принадлежат интервалу (а, b), то
F(x) = 0 при х ≤ а; F(x) = 1 при х ≥ b.
5. Справедливы следующие предельные отношения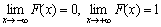 
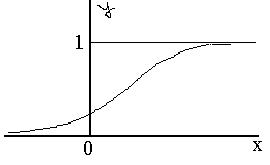
Вероятность попадания случайной величины на заданном участке.
Для определенности условимся левый конец α включать в участок (α, β), а правый нет: α ≤ Х < β.
Выразим вероятность этого события через функцию распределения величины Х. Для этого рассмотрим три события:
событие А, состоящее в том, что X < β;
событие В, состоящее в том, что X < α;
событие С, состоящее в том, что α ≤ Х < β.
Событие А по теореме сложения вероятностей равно А = В + С и его вероятность Р(А) = Р(В) + Р(С) или P(X < β) = P(X < α) + P (α ≤ Х < β). Но вероятность нахождения случайной величины левее некоторой текущей переменной есть ни что иное, как функция распределения:
F(β) = F(α) + P (α ≤ Х < β) откуда
P (α ≤ Х < β) = F(β) - F(α)т.е. вероятность попадания случайной величины на заданный участок равна приращению функции распределении на этом участке. Будем неограниченно уменьшать участок (α, β), полагая, что β→α. В пределе вместо вероятности попадания на участок получим вероятность того, что величина примет отдельно взятое значение α:P(X=α) = limβ→α P(α ≤ Х < β) = limβ→α [F(β) - F(α)]
?11.Плотность распределения случайной величины. Свойства. Вероятность попадания случайной величины на заданный участок.
Случайную величину Х называют непрерывной (непрерывно распределенной) величиной, если существует такая неотрицательная функция p(t), определенная на всей числовой оси, что для всех х функция распределения случайной величины F(x) равна:
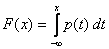. (6.7)
При этом функция p(t) называется плотностью распределения вероятностей непрерывной случайной величины.(f(x))
Если такой функции p(t) не существует, то Х не является непрерывно распределенной случайной величиной.
Таким образом, зная плотность распределения, по формуле (6.7) можно легко найти функцию распределения F(x). И, наоборот, по известной функции распределения можно восстановить плотность распределения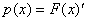 
.
Значит, наряду с функцией распределения, плотность распределения вероятностей непрерывной случайной величины задает ее закон распределения.
1. Плотность распределения – неотрицательная функция:p(t)³0.
Геометрически это означает, что график плотности распределения расположен либо выше оси Ох, либо на этой оси.
2. 
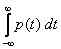=1.
3. P(a<x<b)=F(b)-F(a) - Вероятность попадания случайной величины на заданный участок???
12. Числовые характеристики случайной величины. Центральные моменты. Дисперсия.
Математическое ожидание – среднее значение случайной величины. Сумма произведении всех возможных значений с.в. на вероятности этих значений. Центральный момент первого порядка
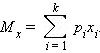
1.Математическое ожидание постоянной величины равно ей самой: M[C]=C, C – постоянная;
2. M[C•X]=C•M[X]
3. Математическое ожидание суммы случайных величин равно сумме их математических ожиданий: M[X+Y]=M[X]+M[Y]
4. Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий: M[X•Y]=M[X]•M[Y], если X и Y независимы.
Для непрерывной сл. величины, заданной функцией плотности вероятности f(x), математическое ожидание определяется в виде интеграла
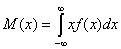
Дисперсией (рассеянием) случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания. Второй центральный момент с.в. Х
D(X)=M(X2)-M2(X)
для непрерывной случайной величины
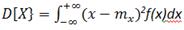
Свойства:
1. D[C]=0, C – постоянная;
2. D[C•X]=C2•D[X]
3. D[X+Y]=D[X]+D[Y]
4. D[X-Y]=D[X]-D[Y]
5. D[X]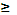 
0
Дисперсия числа появлений в n независимых испытаниях (с одинаковой вероятностью р появления события в каждом испытании и вероятностью не появления события q вычисляется
по формуле
D(X) = n*p*q
Средний квадрат отклонения с.в.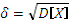 
Число, M[X-M[Xk]], центральный момент порядка k с.в. Х
Вопрос 13. Характеристики случайной величины: центральный момент и дисперсия
· Моменты относительно центра распределения х = m называются центральными моментами и обозначаются: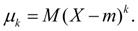 
следует, что центральный момент первого порядка всегда равен нулю: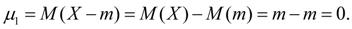 
· Центральные моменты не зависят от начала отсчета значений случайной величины, так как при сдвиге на постоянное значение С ее центр распределения сдвигается на то же значение С, а отклонение от центра не меняется: Х – m = (Х – С) – (m – С).
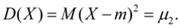
Теперь очевидно, что дисперсия – это центральный момент второго порядка:
· Дисперсией случайной величины х называется математическое ожидание квадрата соответствующей центрированной величены.
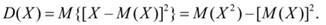
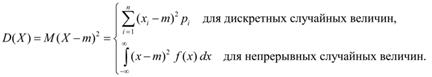Здесь m = М ( Х ).
Свойства дисперсии:
Вопрос14.
1)Биноминальное распределение:
2)Геометрическое распределение.
3)Распределение Пуасона.
15. Законы распределения – равномерный, показательный.
Равномерный закон распределения. Непрерывная случайная величину Х имеет равномерный закон распределения (закон постоянной плотности) на отрезке [a; b], если на этом отрезке функция плотности вероятности случайной величины постоянна, т.е. f(x) имеет вид:
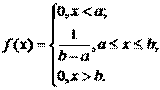
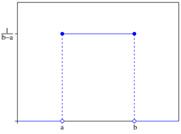
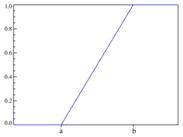
Функция плотности Функция распределения F(x)
вероятности f(x)
Вероятность попадания значения случайной величины, имеющей равномерное распределение, на интервал ), принадлежащий,( целиком отрезку [a, b]:
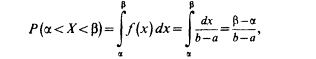
Пример. Время ожидания ответа на телефонный звонок – случайная величина, подчиняющаяся равномерному закону распределения в интервале от 0 до 2 минут. Найти интегральную и дифференциальную функции распределения этой случайной величины.
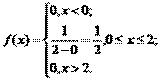
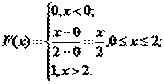
Непрерывная случайная величина Х имеет Показательный (экспоненциальный) закон распределения с параметром λ, если ее плотность вероятности имеет вид
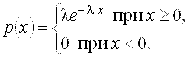
Функция распределения случайной величины, распределенной по показательному закону, равна
Кривая распределения Р(Х) и график функции распределения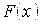 
приведены на рис. 8.13.
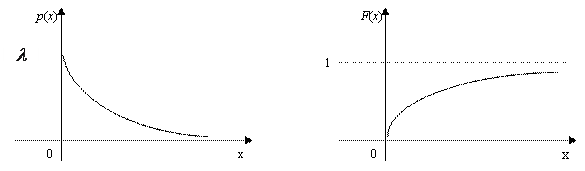
Рис. 8.13
Для случайной величины, распределенной по показательному закону
; 
.
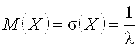Вероятность попадания в интервал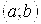 
непрерывной случайной величины Х, распределенной по показательному закону
.
Пример. Непрерывная величина Х распределена по показательному закону
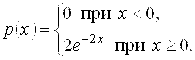
Найти вероятность попадания значений величины Х в интервал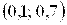 
.
Решение. Поскольку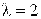 
, то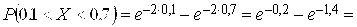 
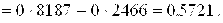
16. Нормальный закон распределения. Параметры нормального закона. Свойства.
Нормальный закон распределения.
Нормальный закон распределения (закон Гаусса). Непрерывная случайная величина Х имеет нормальный закон распределения с параметрам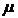и 
и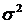 
(обозначают 
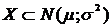), если ее плотность вероятности имеет вид:
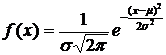где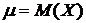 
, 
.
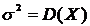Нормальный закон распределения случайной величины Х с параметрам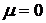и 
и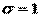 
(обозначается N(0;1)) называется стандартным или нормированным, а соответствующая нормальная кривая – стандартной или нормированной.
Для практических целей очень важны свойства случайной величины, имеющей нормальный закон распределения.
1. Если 
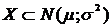, то для нахождения вероятности попадания этой величины в заданный интервал (х1;х2) используется формула:
.
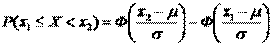2. Вероятность того, что отклонение случайной величины 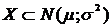от ее математического ожидания 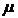не превысит величину 
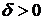(по абсолютной величине), равна:
.
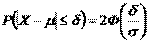3. "Правило трех сигм". Если случайная величина 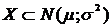, то практически достоверно, что ее значения заключены в интервале ( 
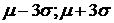). (Вероятность выхода за эти границы составляет 0,0027.) Правило позволяет, зная параметры ( 
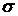и 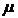), ориентировочно определить интервал практических значений случайной величины.
Пример 5. Случайная величина распределена нормально с параметрами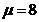 
, 
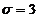. Найти вероятность того, что случайная величина в результате опыта примет значение, заключенное в интервале (12,5; 14).
.
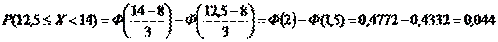Вопрос 17:
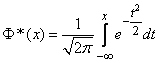данная функция представляет собой, функцию распределения для нормально распределенной случайной величины с параметрами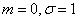 
Условимся называть функцию нормальной функцией распределения.
вероятность попадания случайной величины х на интервале от а до в: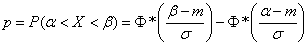 
Таким образом, мы выразили вероятность попадания на участок случайной величины х, распределенной по нормальному закону с любыми параметрами, через стандартную функцию распределения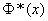 
, соответствующую простейшему нормальному закону с параметрами 0,1. Заметим, что аргументы функции 
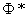в данной формуле имеют очень простой смысл: 
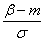есть расстояние от правого конца участка 
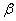до центра рассеивания, выраженное в средних квадратических отклонениях; 
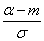- такое же расстояние для левого конца участка, причем это расстояние считается положительным, если конец расположен справа от центра рассеивания, и отрицательным, если слева.
Свойства функции:
1. 
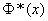
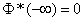
2. 
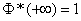
3. 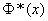- не убывающая функция.
Кроме того, из симметричности нормального распределения с параметрами 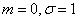относительно начала координат следует, что 
.
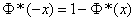На практике часто встречается задача вычисления вероятности попадания нормально распределенной случайной величины на участок, симметричный относительно центра рассеивания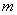 
. Рассмотрим такой участок длины 
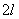. Вычислим вероятность попадания на этот участок по формуле 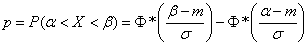получим:
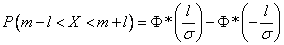
· Учитывая свойства функции 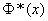,данная формула примет более компактный вид, получим формулу для вероятности попадания случайной величины, распределенной по нормальному закону на участок, симметричный относительно центра рассеивания: 