Министерство образования республики Беларусь

Дата: 2025-06-14; Просмотры: 1

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

УЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ

"БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТРАНСПОРТА"

Кафедра "Информационные технологии"

КОНТРОЛЬНАЯ РАБОТА

по дисциплине

"Информатика"

Вариант 3

Гомель, 2021

Оглавление

Задание 1. 3

Задание 2. 5

Задание 3. 6

Задание 4. 8

Задание 5. 10

Список использованных источников. 12

Задание 1

Средствами MathCAD решить уравнение с точностью 10^-5: Отделить корень графически и уточнить его с помощью функции root; блока Given … Find; блока Given … Minerr.

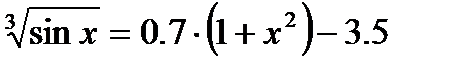
Решение:

Решение данного уравнения будем проводить в два этапа:

1) отделение корней уравнения графически;

2) уточнение корней уравнения.

Определим функцию f(x), равную правой части заданного уравнения, когда левая часть равна нулю:

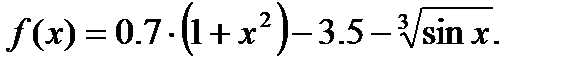
Вставим в документ графическую область. Для этого выберем дважды пиктограмму с изображением графика сначала на панели Math (Математика), затем на палитре графиков Graph или выполним из главного меню последовательность команд Insert / Graph / X-Y Plot (Вставка / График / X-Y Зависимость). Снизу по оси абсцисс наберём x, а сбоку по оси ординат введём f(x). Для появления графика щелкнем левой клавишей мыши вне графической области.

Отформатируем график функции f(x). Для этого щелкнем правой клавишей мыши в области графика и выберем в контекстном меню команду Format (Формат). Установим отображение осей графика по центру, добавим линии сетки по координатным осям. Отменим при этом автосетку и установим количество линий сетки, равное 10.

Для подтверждения внесенных изменений нажмем последовательно кнопки «Применить» и «ОК». После указанных преобразований получим график функции f(x), который представлен на рисунке 1.1.

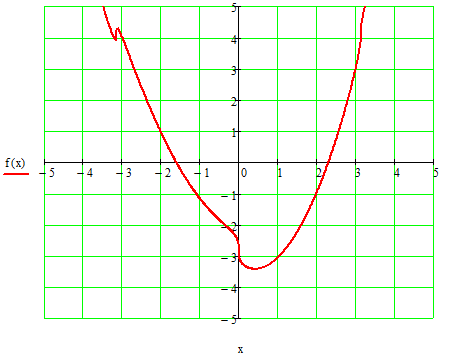
Рисунок 1.1 – График функции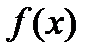

На основании графика делаем вывод, что заданное уравнение имеет два корня, которые находятся на следующих интервалах: 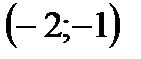и .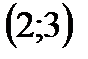

Поиск корней заданного уравнения представлен на рисунке 1.2.

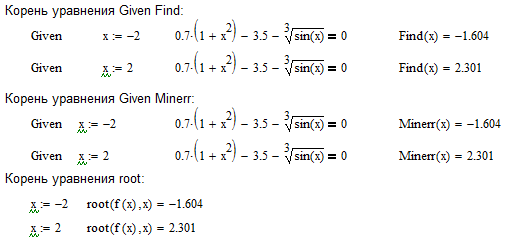
Рисунок 1.2 – Поиск корней заданного уравнения

Задание 2

Средствами MathCAD решить полиномиальное уравнение:

.

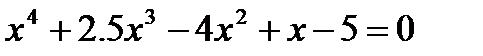Решение:

Напечатаем левую часть уравнения, не приравнивая выражение к 0, и выделим синим курсором переменную x.

Выберем из главного меню Symbolics / PolynomialCoefficients (Символика / Коэффициенты полинома). Появившийся вектор коэффициентов полинома выделим целиком синим курсором и вырежем в буфер обмена, используя кнопку «Вырезать» на панели инструментов Formatting (Форматирование) или комбинацию клавиш «Ctrl+X». Напечатаем «v:=» и вставим вектор из буфера обмена, используя кнопку «Вставить» на панели инструментов или комбинацию клавиш «Ctrl + V».

Для получения результата напечатаем polyroots(v). Фрагмент решения заданной задачи представлен на рисунке 2.1.

Рисунок 2.1 – Поиск корней заданного уравнения

Задание 3

Средствами MathCAD решить систему линейных алгебраических уравнений с помощью блока Given … Find и матричным способом.

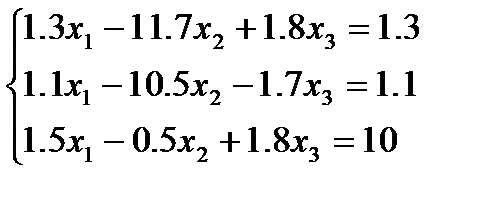
Решение:

Найдем решение системы уравнений, при помощи блока Given … Find. Зададим всем неизвестным, входящим в систему уравнений, произвольные начальные приближения, например: x 1:=0, x 2:=0, x 3:=0.

Напечатаем слово Given. Установим курсор и наберём уравнения системы, каждое в своем блоке. Используем при этом логический знак равенства (Ctrl + =).

После ввода уравнений системы напечатаем X:=Find(x1, x 2, x 3) и получим решение системы в виде вектора, состоящего из трех элементов (рисунок 3.1)

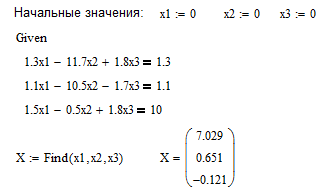
Рисунок 3.1 – Решение системы уравнений

Решим систему линейных уравнений матричным способом. Создадим матрицу А, состоящую из коэффициентов при неизвестных системы. Для этого напечатаем «A:=» , вызовем окно создания массивов (Ctrl+M). Число строк (Rows) и столбцов (Columns) матрицы данной системы равно 3. Заполним пустые места шаблона матрицы коэффициентами при неизвестных системы (рисунок 3.2).

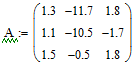
Рисунок 3.2 – Определение матрицы A

Зададим вектор B свободных членов системы. Сначала напечатаем «B :=», затем вставим шаблон матрицы(Ctrl + M), где количество строк (Rows) равно 3, а количество столбцов (Columns) равно 1. Заполним его (рисунок 3.3).

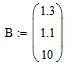
Рисунок 3.2 – Определение вектора B

Решим систему матричным способом (рисунок 3.3).

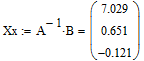
Рисунок 3.3 – Решение системы уравнений

Для проверки правильности решения системы, полученного матричным способом, достаточно вычислить произведение A * X, которое должно совпасть с вектором-столбцом свободных членов B (рисунок 3.4)

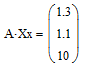
Рисунок 3.4 – Проверка правильности решения

Совпадает, значит, решение найдено правильно.

Задание 4

Решить уравнение в MS Excel, отделив его корни аналитически и графически и уточнив один из них с точностью 0.0001, используя инструмент Подбор параметра. Проверить правильность решения уравнения.

.

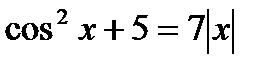Решение:

Запустив MS Excel, переименуем листы рабочей книги в Задание 4, Задание 5.

Для графического отделения корней построим таблицу значений нашей функции. Для этого в ячейку А1 введём заголовок столбца «X», в ячейку В1 заголовок столбца «Y». Искать корни будем на отрезке [-3; 3]. В ячейку А2 вводим «-3», а в ячейку А3 вводим формулу «=А2+0.1» и с помощью маркера автозаполнения заполняем до ячейки А62.

Далее в ячейку В2 вводим формулу «=COS(A2)^2+5-7*ABS(A2)» и также с помощью маркера автозаполнения заполняем ячейки до В62 включительно.

Теперь построим график. Для этого выделяем диапазон «=A1:B62» и выбираем на вкладке Вставка Диаграммы – Точечные с гладкими кривыми. На листе появляется наш график (рисунок 4.1).

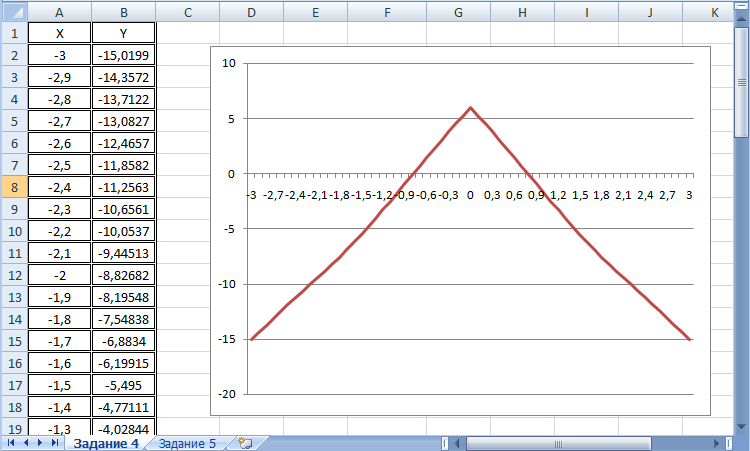
Рисунок 4.1 – Отделение корней уравнения

Как видно из таблицы один корень лежит в интервале (-0.9;0.6), второй – (0.6;0.9). Уточним первый корень. Скопируем начальное значение и формулу в ячейки «F 20: G 20» в которых и будем подбирать.

На вкладке данные, в группе «Работа с данными», раскрываем «Анализ что-если» и выбираем команду «Подбор параметра».

Установить в ячейке: в поле указывается адрес ячейки, в которой записана формула правой части функции(F 20); значение: в поле указывается значение, которое должен получить полином в результате вычислений, т.е. правая часть уравнения (в нашем случае 0); Изменяя значение: в поле указывается адрес ячейки (где записано начальное приближение), в которой будет вычисляться корень уравнения и на которую ссылается формула (F 20).

Аналогично делаем и для другого корня. Подбор параметра представлен на рисунке 4.2.

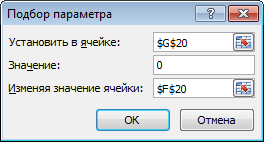
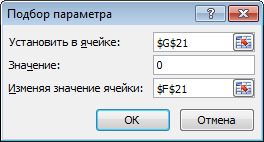
Рисунок 4.2 – Подбор параметра

В результате получили следующие корни (рисунок 4.3)

Рисунок 4.3 – Корни уравнения

Задание 5

В MS Excel найти решение системы линейных уравнений: задать матрицу коэффициентов при неизвестных системы и столбец свободных членов. Вычислить определитель матрицы коэффициентов при неизвестных и решить систему уравнений методом обратной матрицы. Сделать проверку.

.

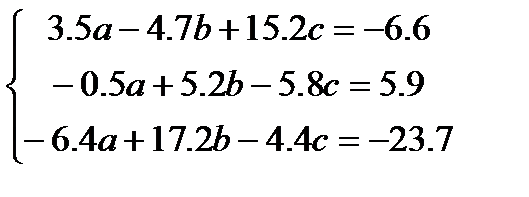Решение:

В ячейки «В2: D 4» вводим коэффициенты системы. В ячейки «G 2: G 4» вводим значения свободных членов (рисунок 5.1).

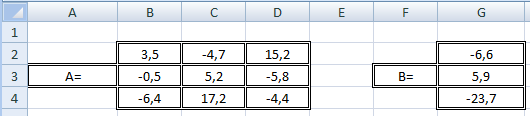
Рисунок 5.1 – Определение матрицы A и вектора B

Найдём определитель матрицы. В ячейку «С7» вставляем формулу «=МОПРЕД(B2:D4)» (рисунок 5.2).

Рисунок 5.2 – Определитель матрицы

Так как определитель равен 480.092≠0, то система имеет решение.

Матричный способ решения СЛАУ достаточно прост. Обе части матричного равенства AX=B умножим слева на обратную матрицу А^-1. Получим A^-1´A´X=A^-1´ b. Т.к. A^-1´A=E, где E – единичная матрица (диагональная матрица, у которой по главной диагонали расположены единицы). Тогда решение системы запишется в следующем виде X = A^-1´ b . Т.е. для решения системы необходимо найти для матрицы A обратную A^-1 и умножить её справа на вектор-столбец b свободных членов.

Обратную матрицу находим с помощью функции «МОБР()». Данная функция возвращает блок ячеек, поэтому должна вводиться формула массива (Ctrl+Shift+Enter). Обратная матрица представлена на рисунке 5.3.

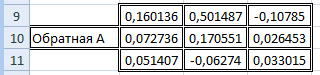
Рисунок 5.3 – Обратная матрица

Затем вычисляем вектор Х=А^-1*b. Для умножения используем функцию «МУМНОЖ()» (рисунок 5.4).

Рисунок 5.4 – Корни системы уравнений

Для проверки умножим матрицу А на вектор-столбец Х (рисунок 5.5).

Рисунок 5.5 – Проверка решения системы уравнений

Результат совпадает с вектором столбцом b, следовательно, найденное решение верное.

Список использованных источников

1 Борисенко, М. В. Основы информационных технологий : пособие / М. В. Борисенко. – Гомель : БелГУТ, 2005. – 180с.

2 Голдобина, T. А. Mathcad для экономистов: практикум / T. А. Голдобина. – Гомель : БелГУТ, 2007. – 107с.

3 Гораев, О. П. Операционная система WINDOWS. Операционные оболочки: практикум по компьютерным технологиям / О. П. Гораев, Ю. П. Лыч. – Гомель: БелГУТ, 2003. – 68с.

4 Гораев, О.П. Табличный процессор MS EXCEL: практикум по компьютерным технологиям/О. П. Гораев, Ю. П. Лыч. – Гомель : БелГУТ, 2003. – 67с.

5 Гораев, О.П. Текстовый процессор MS WORD: практикум по компьютерным технологиям /О.П. Гораев, Ю.П. Лыч. – Гомель : БелГУТ, 2003. – 68с.

6 Дьяконов, В. П. Энциклопедия Mathcad 2001i и Mathcad 11 / В. П. Дьяконов. − М. : СОЛОН-Пресс, 2004. − 832с.

7 Информатика. Базовый курс : учеб. пособие для студ. высш. техн. учеб. заведений / С. В. Симонович [и др.] ; под общ. ред. С. В. Симоновича. – СПб. : Питер, 2003. − 640с.

8 Информатика. Программирование на языке Паскаль : практикум по лабораторным работам. Ч. 1 / А. П. Кейзер [и др.] ; под общ. ред. Ю. А. Пшеничнова. – Гомель : БелГУТ, 2005. – 46 c.

9 Кирьянов, Д. В. Самоучитель Mathcad 13 / Д. В. Кирьянов. − СПб. : БХВПетербург, 2006. − 560с