Крутильные колебания

Дата: 2025-05-25; Просмотры: 3
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

 

Крутильными колебаниями называются такие колебания, прикоторых твердое тело, подвешенное на невесомой вертикальной нити, совершает колебания в горизонтальной плоскости.

В случае малых углов j при крутильных колебаниях на тело действует возвращающий момент

 

М = -Dj,

 

где D - модуль кручения нити подвеса.

Учитывая выражение (3), запишем уравнение движения при крутильных колебаниях:

 

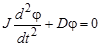, (4)

 

J - суммарный момент инерции, который включает момент инерции исследуемого тела и подвеса крутильного маятника. Решение этого дифференциального уравнения можно представить:

 

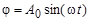, (5)

 

А0 - амплитуда колебаний. Взяв вторую производную от (5) и подставив ее и j в (4), получим:

 

,

 

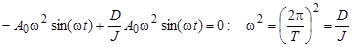а период крутильных колебаний определиться как:

 

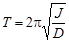. (6)

 

 

Теория метода

 

Для расчета момента инерции тела относительно произвольной оси (формула 6а) необходимо знать момент инерции подвеса крутильного маятника и модуль кручения. Для определения этих величин, измеряют период крутильных колебаний для двух случаев:

1) без дополнительного груза T1;

2) с дополнительным грузом Т2 (цилиндром) , момент инерции которого легко рассчитать теоретически (например цилиндра):

 

.

 

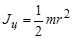Запишем период крутильных колебаний для этих случаев:

 

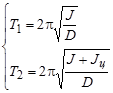(7)

 

где Jц - момент инерции цилиндра, D - модуль кручения, J - момент инерции подвеса крутильного маятника.

Возьмем оба уравнения в квадрат и разделим друг на друга:

 

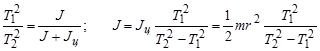. (8)

 

Подставим (8) в первое уравнение системы (7) и разрешим относительно D

 

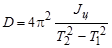. (9)

 

Рассчитав модуль кручения и момент инерции подвеса можно преобразить вторую формулу в системе (7), в которой вместо Jц уже стоит искомый момент инерции тела Jx .

 

:

 

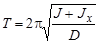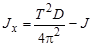. (10)

 

При упрощенном D и J получите у преподавателя.

 

 

Порядок выполнения работы

 

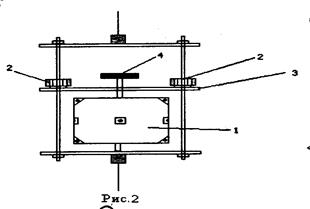
1. Установите исследуемое тело. Для этого отверните цанговые зажимы 2 (рис.2) и установите планку 3 на необходимую высоту, закрутите цанговые зажимы 2, винтом 4 закрепите исследуемое тело вдоль заданной оси.

Рис.2

2. Включите секундомер и обнулите индикаторы, для чего нажмите последовательно кнопки "стоп" и "сброс" (кнопка "пуск" отжата).

3. Подведите к электромагниту маятник.

4. Нажмите кнопку "пуск". Отсчитайте заданное преподавателем количество колебаний N (кнопку "стоп" нажать, когда произойдет N - 1 колебаний). По формуле 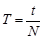рассчитайте период колебаний (t - время, N - число колебаний).

5. Определите момент инерции твердого тела относительно произвольной оси по формуле (10).

 

№ N t T J DJ 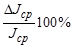Jист
1 2 3              

Среднее значение

        

 

Контрольные вопросы

 

1. Физический смысл момента инерции.

2. Момент инерции материальной точки, твердого тела.

3. Дифференциальное уравнение крутильных колебаний. Его решение.

4. оновное уравнение динамики вращательного движения.

5. Момент силы, его уравнение.

6. Цель работы. Вывод рабочей формулы.