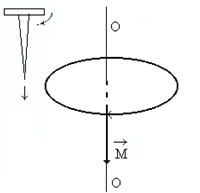
Изменение момента импульса тела dL равно импульсу момента силы.
| |
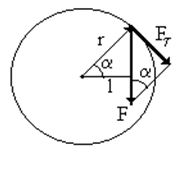
Момент силы - величина векторная, численно равная произведению силы на плечо 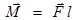 . Плечом называется кратчайшее расстояние от оси вращения до линии действия силы (рис.2).
. Плечом называется кратчайшее расстояние от оси вращения до линии действия силы (рис.2).
|
Рис.3 |
Момент силы параллелен оси вращения (рис.3) и направлен вдоль нее так, что если буравчик вращать так, как вращается тело, то поступательное движение буравчика покажет направление момента силы..
| Рис.2 |
Из рис. 2 видно, что 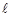 = rsin a, где r - радиус вектор точки приложения силы
= rsin a, где r - радиус вектор точки приложения силы
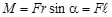 . (1)
. (1)
Или в векторной форме 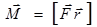
Подставим в (1) выражение силы из второго закона Ньютона, и учтем, что угловое ускорение e связано с ускорением аt = e r, получим, а Ft=F sina
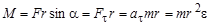
Но mr2 есть момент инерции I, и окончательно получим
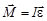 или
или 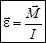 (2)
(2)
Полученное выражение является основным уравнением динамики вращательного движения. Момент силы равен произведению момента инерции на угловое ускорение. Данное уравнение можно преобразовать:
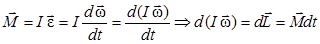
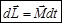 (3)
(3)
Изменение момента импульса тела dL равно импульсу момента силы.
Это есть вторая форма основного уравнения динамики вращательного движения.
Крутильные колебания - это такие колебания, которые совершает подвешенное твердое тело вокруг вертикальной невесомой нити, верхний конец которой закреплен (рис.4).
Применим к этим колебаниям основное уравнение вращательного движения. При крутильных колебаниях на тело действует возвращающий момент со стороны нити подвеса, обусловленный упругими силами.
|
Рис.4 |
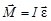 и
и 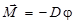 , тогда
, тогда
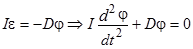 ,
,
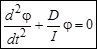 . (4)
. (4)
Полученное уравнение является дифференциальным уравнением крутильных колебаний , в этом уравнении отношение D / I= w2 - циклическая частота.
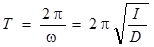 . (5)
. (5)
Решением уравнения (4) является
j = j0sin(wt + f)
где f-начальная фаза колебаний(угол отклонения в момент времени t=0), j0 - максимальный угол поворота.
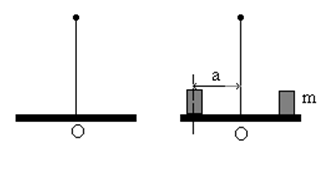
Вывод рабочей формулы. Воспользуемся методом крутильных колебаний для определения момента инерции диска, подвешенного на упругой нити (рис.4). Для этого воспользуемся периодом крутильных колебаний по формуле (5) . Однако в этой формуле две неизвестные величины: I- момент инерции диска относительно оси О, проходящей через центр масс диска, и D- модуль упругости нити. Учитывая аддитивные свойства момента инерции, поставим на диск два груза и запишем второе уравнение
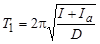 , (6)
, (6)
где Ia - момент инерции двух грузов относительно оси О. Возведем (5,6) в квадрат и разделим одно уравнение на другое:
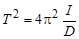 ,
,
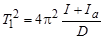
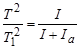 .
.
Выразим момент инерции диска
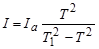 .
.
Момент инерции двух грузов относительно оси О по теореме Штейнера равен:
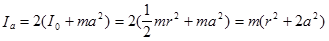 ,
,
где I0 - момент инерции цилиндра относительно его оси, проходящей через центр масс. Подставим полученное выражение в предыдущую формулу и получим:
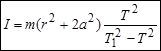 , (7)
, (7)
где r - радиус цилиндра, a - расстояние между осями диска и цилиндра.
Выражение (7)- является рабочей формулой для расчета момента инерции диска.
Выполнение работы
1. Запустите крутильные колебания и дайте им успокоиться, измерьте время t заданного числа колебаний. Найдите период колебаний диска без грузов 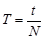 , где N- число колебаний.
, где N- число колебаний.
2. Поставьте на диск цилиндры, измерьте время t 1 и период T 1 с грузами.
3. По рабочей формуле рассчитайте момент инерции диска.
| № | t, c | T, c | t1,c | T1,c | I, кг м2 | D I, кг м2 | 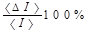
|
| Среднее значение | |||||||
 Контрольные вопросы
Контрольные вопросы
1. Цель работы.
2. Вывод рабочей формулы.
3. Физический смысл момента инерции твердого тела и материальной точки.
4. Теорема Штейнера.
5. Где при выводе рабочей формулы использовалась теорема Штейнера. Когда применяется эта теорема.
6. Основное уравнение динамики вращательного движения.
7. Вывод дифференциального уравнения крутильных колебаний.
8. Момент силы. Направление момента силы.
Лабораторная работа № 1.6
Измерение ускорения силы тяжести с помощью оборотного
маятника
Приборы и принадлежности: оборотный маятник, секундомер, линейка, опорная призма.
Краткая теория
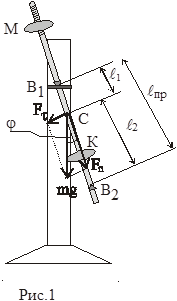 Физический маятник – твердое тело, которое совершает колебания вокруг горизонтальной оси, не проходящей через центр масс (рисунок). В положении равновесия вращающий момент силы тяжести равен нулю, так как плечо этой силы равно нулю. При отклонении от положения равновесия на угол j (рисунок) возникает вращающий момент, равный
Физический маятник – твердое тело, которое совершает колебания вокруг горизонтальной оси, не проходящей через центр масс (рисунок). В положении равновесия вращающий момент силы тяжести равен нулю, так как плечо этой силы равно нулю. При отклонении от положения равновесия на угол j (рисунок) возникает вращающий момент, равный
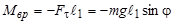 . (1)
. (1)
При малых углах (j »50) sinj » j и тогда 

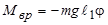 . (2)
. (2)
Минус означает, что вращающий момент стремится вернуть маятник в положение равновесия. Из основного уравнения динамики вращательного движения вращающий момент 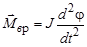 , подставив в (2), получим
, подставив в (2), получим
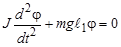 . (3)
. (3)









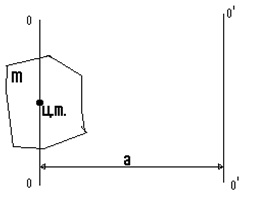 Рис.1
Рис.1