Контрольные вопросы

Дата: 2025-05-25; Просмотры: 2
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

1.Какое движение называется механическим колебанием ?

2.Какие колебания называются гармоническими ? Запишите уравнение этих колебаний. Дайте определение кинематическим элементам колебаний.

3.Изобразите график гармонических колебаний.

4.Запишите силы , действующие при свободных колебаниях. С учетом этих сил составьте дифференциальное уравнение свободных колебаний.

5.Запишите решение дифференциального уравнения гармонических колебаний.

6.Что называется математическим маятником ? Какие колебания он совершает ? Изобразите силы , под действием которых колеблется маятник.

7.Выведите формулу периода колебаний математического маятника.

8.Обьясните причину зависимости ускорения силы тяжести от широты географической широты , сделайте рисунок.

9.Выведите рабочую формулу.

 

Литература

 

1.А.А.Детлаф,Б.М.Яворский, Курс физики. Т.1,1973, с.152.

2.Г.А.Зисман, О.М.Тодес. Курс общей физики. Т.,1974, с.258.

3.С.Э.Фриш, А.В.Тиморева. Курс общей физики. Т.1, 1961, с.381.

 

Лабораторная работа 1.5

Определение момента инерции тела методом крутильных

колебаний

Приборы и принадлежности: кронштейн с закрепленной проволокой, испытуемое тело, два цилиндра, секундомер, штангенциркуль.

Краткая теория

Основными характеристиками динамики вращательного движения являются: момент инерции и момент силы.

Момент инерции есть мера инертности тела, имеющего ось вращения .

Во вращательном движении момент инер­ции имеет такую же роль, как масса при поступательном движе­нии. Как и масса, мо­мент инерции относи­тельно оси вращения скалярная величина. Однако величина момента инерции тела зависит от положения оси вращения.

Момент инерции материальной точки относительно оси вращения, находящейся на расстоянии r, равен произведению массы на квадрат расстояния до оси вращения .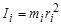

Момент инерции твердого тела равен сумме моментов инерции его составных точек 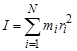. В случае непрерывного тела момент инерции тела относительно заданной оси представится выражением .

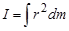Момент инерции относительно произвольной оси, не проходящей через центр масс, можно вычислить по теореме Штейнера:

Момент инерции относительно произвольной оси равен сумме момента инерции тела относительно оси, проходящей через центр масс параллельно заданной оси и произведения массы на квадрат расстояния между осями (Рис.1).