Частотой гармонических колебаний n называется число колебаний в единицу времени.
Лабораторная работа 1.4
Определение ускорения силы тяжести
математическим маятником
Краткая теория
Колебательным движением (колебанием) называется процесс, при котором система, многократно отклоняясь от своего состояния равновесия, каждый раз вновь возвращается к нему.
Колебания называются периодическими, если материальная точка возвращается в исходное состояние через равные промежутки времени. Время одного полного колебания называется периодом колебания Т.
Величина, обратная периоду, называется частотой: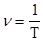 
.
Частотой гармонических колебаний n называется число колебаний в единицу времени.
Максимальное отклонение точки от положения равновесия называется амплитудой колебания А.
Существует множество различных видов периодических колебаний. Простейшими колебаниями будут такие, при которых координата материальной точки изменяется с течением времени по закону синуса или косинуса. Такие колебания называются гармоническими .
x = A sin (wt + j ), (1)
где х - смещение точки (координата),
А - амплитуда колебаний ,
(wt+j ) - фаза колебаний ,
w - циклическая частота ,
j - начальная фаза .
Математический маятник
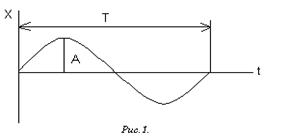
Математическим маятником называется материальная точка, подвешенная на невесомой нерастяжимой нити ( рис.2 ).
В положении равновесия сила тяжести Р уравновешивается силой натяжения нити N. Если отклонить маятник на малый угол a, то P и N будут направлены под углом друг к другу и не уравновешены. Равнодействующей этих сил будет составляющая F силы тяжести Р которая является возвращающей силой и равна : 
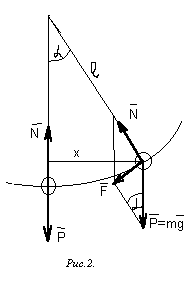
F = -mg sina
Знак минус указывает на противоположность направлений силы F и смещения х .
При малых углах отклонения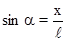 
. Поэтому : 
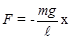; Из закона Гука 
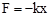, где 
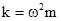- коэффициент упругости следует, что величина 
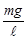подобна коэффициенту упругости k в упругой силе, т.е.
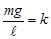или 
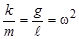. (3)
Тогда период колебания математического маятника равен :
, 
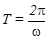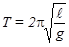. (4)
Значение величины периода колебаний Т используется для определения ускорения силы тяжести g :
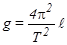. (5)
На измерении g основаны методы определения формы Земли и гравиметрическая разведка (поиски руд , каменного угля , нефти и др.)
Зависимость ускорения силы тяжести от географической
широты
Известно, что ускорение g зависит от географической широты j по двум причинами , являющимся следствием вращения Земли вокруг оси : 1) сплюснутостью Земли с полюсов , 2) возникновением центростремительной силы. По первой причине полярный радиус меньше, чем экваториальный. Поэтому все тела на полюсе испытывают притяжение к центру Земли большее , чем на экваторе. Однако это различие мало.
Основной причиной зависимости g от j является вторая причина. Вследствие вращения Земли на всякое тело, лежащее на поверхности на широте j, действует центростремительная сила:
Fц = mw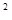 
r = mw2Rcos j, ( 6 )
направленная к оси вращения О’ . В связи с этим целесообразно разложить силу тяготения F 2 на ценростремительную силу F ц и силу тяжести Р (рис.3).
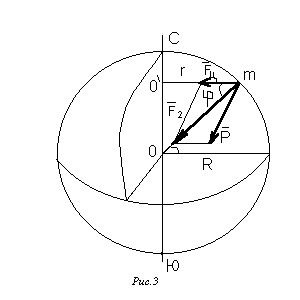
Таким образом, сила тяжести Р несколько отклоняется от F 2. Но если учесть, что это отклонение незначительное, то силу тяжести Р можно найти вычитанием из силы F 2 проекции центростремительной силы F ц на направление F 2 :
P = F2 -Fц cos j.
Или учитывая ( 6 ) , получим:
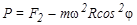. ( 7 )
Подставляя в уравнение ( 7 ) значения
P = mgj,
F2=mg90 ( j полюса = 90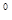 
) и сокращая уравнение на m , имеем :
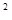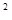gj= g90 - w R cos j.
Теория метода
Из формулы периода колебаний маятника 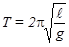легко найти ускорение силы тяжести
.
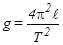Непосредственное измерение длины маятника представляет определенную трудность , так как приходится определять положение центра тяжести шарика и точки подвеса. Поэтому берут маятник произвольной длины и определяют период колебания
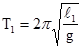. (8)
Затем укорачивают маятник и, измерив уменьшение длины, вновь определяют период колебания
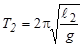. (9)
Вычтя ( 8 ) из ( 9 ) и решив уравнение относительно g, получим
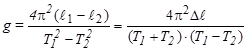. ( 9 )
Таким образом, отпадает необходимость измерять длину маятника , достаточно определить разность длин.
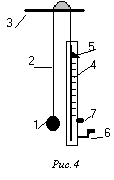
В данной работе (см. рис.4) маятником служит тяжелый шар 1 , подвешенный на длинной нити 2 к кронштейну 3 , укрепленному на стене. Параллельно нити укреплена линейка 4, с миллиметровыми делениями, по которой перемещается движок 5. По этой линейке возможно произвести отсчет разности длин маятника. Ручка 6 служит для изменения длины маятника. При изменении длины маятника нажмите фиксатор 7.
Порядок выполнения работы
1. С помощью ручки 6 устанавливают длину маятника l1 , при этом отмечают положение движка 5 на линейке 4.
2. Отводят маятник от положения равновесия на небольшой угол ( около 5-6 ). Отпускают шар , предоставив ему свободно колебаться.
3. В момент наибольшего отклонения маятника пускают в ход секундомер и отсчитывают время t1 , в течение которого маятник совершит n1=50 полных колебаний. Измерения времени 50 колебаний для неизменной длины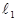 
проводят три раза и результаты записываются в таблицу.
4. Устанавливают новую длину маятника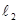 
и отмечают новое положение движка на линейке.
5. Для новой длины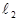 
измеряют время n2=50 полных колебаний. Измерения проводят три раза.
6. По результатам измерений t1 и t2 времени полных колебаний рассчитываются периоды колебаний T1 и T2 по формуле: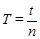 
, где t - время , n - число колебаний .
7. Разность между двумя положениями движка есть разность длин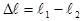 
.
8. По формуле ( 9 ) вычисляют ускорение силы тяжести.
Отчетная таблица
| № | t1,c | n1 | T1,c | t2, c | n2 | T2,c | Dl м | g ,м/с2 | |
| 1 2 3 | |||||||||
|
| |||||||||
Среднее значение