Определение момента инерции махового колеса и силы трения в опоре
Лабораторная работа № 1.2
Определение момента инерции махового колеса и силы трения в опоре
Краткая теория
Вращательным движением твердого тела называется такое движение, при котором траектории всех точек тела являются концентрическими окружностями с центрами на одной прямой, называемой осью вращения.
Вращательное движение характеризуется угловой скоростью вращения w и угловым ускорением e, которые определяются по формулам:
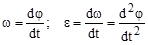, (1)
где j- угол поворота тела.
Связь между линейной v и угловой w скоростями, линейным аt и угловым e ускорениями следующая:
(2)
Векторы, характеризующие параметры вращательного движения, направлены по оси вращения
 |
.
Вектор угловой скорости определяет :
1. Величину угловой скорости
2. Плоскость вращения
3. Направление вращения.
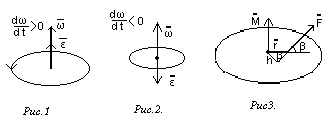
Длина вектора w определяет величину угловой скорости; он проводится по оси вращения (перпендикулярно плоскости вращения, и определяет плоскость вращения ), а направление вращения (вращение по часовой стрелке или против, вектор направлен вверх или вниз ) определяется правилом буравчика. (рис.1).
Если буравчик вращать так, как вращается тело, то поступательное движение буравчика покажет направление вектора угловой скорости.
Если вращение переменное, то вектор углового ускорения проводится по оси вращения. Если угловая скорость возрастает, то направление углового ускорения совпадает с угловой скоростью, в противном случае - направление противоположно (рис.1,2,3).
Закон сохранения энергии: В замкнутой системе энергия не исчезает и не возникает. Она только переходит из одной формы в другую.
Частным случаем этого закона является закон сохранения полной механической энергии: В замкнутой системе консервативных сил полная механическая энергия остается неизменной:
Екин+Епот = сonst ,
где Екин=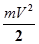 
- кинетическая энергия, которой обладает любое тело массы m, движущееся со скоростью V ;
Епот= mgh - потенциальная энергия тела, она определяется взаимным расположением тел.
Консервативными силами называются силы, работа которых не зависит от формы траектории, а зависит только от начального и конечного положения тела. Например, силы упругости, тяготения.
Диссипативными силами называют силы работа, которых зависит от длины и формы траектории. Например, силы трения.
Если в системе присутствуют диссипативные силы, часть механической энергии переходит в тепловую.
Моментом инерции тела относительно данной оси вращения называется физическая величина, характеризующая меру инертности тела при изменении угловой скорости под действием вращающего момента. Момент инерции тела относительно данной оси вращения является величиной скалярной.
Моментом инерции материальной точки относительно произвольной оси называется произведение массы m этой точки на квадрат расстояния до оси:
.
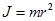Момент инерции твердого тело относительно какой-либо оси равен сумме моментов инерции всех точек тела относительно этой оси:
.
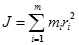Для сплошного тела момент инерции относительно какой-либо оси вычисляется:
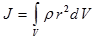где r-плотность, dV- элементарный объем.
Так как момент инерции зависит от оси вращения, то при определении момента инерции необходимо указывать ось вращения
Вращающееся тело обладает кинетической энергией вращательного движения:
.
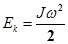Теория метода и описание установки
Приборы и принадлежности: стойка, на которой закреплено маховое колесо, линейка, секундомер, шнур с грузом.
Целью работы является определение момента инерции махового колеса и силы трения в опоре.
Момент инерции махового колеса А и силу трения вала С в опоре можно определить при помощи прибора, изображенного на рис.4.
Маховое колесо приводится во вращательное движение грузом В. Груз В в начальный момент времени находится на высоте h1, обладая потенциальной энергией mgh1, где m- масса груза. Если предоставить возможность грузу падать с высоты h1, то потенциальная энергия груза перейдет в кинетическую энергию поступательного движения груза 
, кинетическую энергию вращательного движения махового колеса 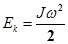, и на работу по преодолению трения в опоре вала, 
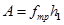. По закону сохранения энергии:
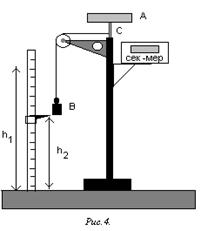
mgh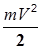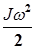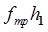1= 
+ 
+ 
. (1)
Груз движется равноускоренно без начальной скорости, скорость и ускорение выразятся:
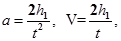(2)
Угловая скорость махового колеса определится:
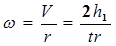, (3)
где r - радиус вала, на который наматывается шнур груза.
Сила трения fтр вычисляется следующим образом. Маховое колесо, вращаясь по инерции, поднимает груз на высоту h2<h1 и потенциальная энергия груза на высоте h2 будет равна mgh2 . Груз не поднимается на первоначальную высоту, так как часть энергии тратится на работу по преодолению трения в опоре:
| № опыта | r, м | m, кг | h1, м | h2. м | t, c | fтр , н | J |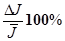 
| Jист |
|
|
|
|
| ||||||
| Среднее значение |
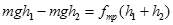. (4)
Откуда сила трения равна:
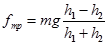. (5)
Подставим в (1) выражения для V,w,fтр из (2,3,5) получим:
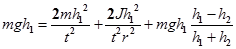
преобразовав, получим:
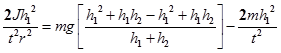
Окончательно рабочая формула :
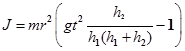. (6)
Измерение и обработка результатов
1. Наматывают на вал С шнур и поднимают груз на высоту h1.
2. Поворачивают рычаг и отпускают груз, при этом включается секундомер - измеряют время падения груза с высоты h1.
3. Определяют высоту h2, на которую поднимется груз после опускания.
4. Измерив радиус вала r, вычисляют силу трения по формуле (5) и момент инерции махового колеса по формуле (6)
Полученные результаты заносят в таблицу
Контрольные вопросы:
1. Закон сохранения энергии. Закон сохранения полной механической энергии. Какой из этих законов не выполняется в лабораторной работе и почему ?
2. Консервативные и диссипативные силы. Примеры этих сил.
3. Цель работы.
4. Физический смысл момента инерции.
5. Момент инерции материальной точки, твердого тела.
6. Размерность момента инерции.
6. Применить закон сохранения энергии к лабораторной установке.
7. Вывести рабочую формулу.
8. Угловая скорость. Угловое ускорение. Вектор угловой скорости и ускорения.