Описание установки
Коэффициент a в первом приближении зависит от материала и для большинства твердых тел имеет порядок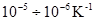 
. В действительности он несколько зависит от температуры.
Если тело изотропно, коэффициент объемного расширения av = 3a,
Vt = V0 ( 1+ avt)
В чем причины теплового расширения тел? Большинство тел имеет кристаллическую структуру , рассмотрим эти причины на примере кристаллических тел.
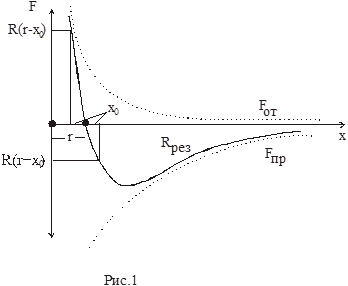
В узлах кристаллической решетки металлического кристалла находятся положительные ионы металла. Между ними беспорядочно , подобно молекулам газа , двигаются электроны. На рис.1 приведены графики сил взаимодействия между частицами в твердых телах.
|
На расстоянии r силы притяжения Fпр. и отталкивания Fотт. взаимно уравновешиваются. R (r) - равнодействующая этих сил. При увеличении температуры увеличивается амплитуда тепловых колебаний атома решетки. Сделав предположение , что отклонение иона в одну и другую сторону от положения равновесия r одинаковы, т.е.,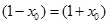 
,получим из графика ( рис.1 ): R(r-x0) ¹ R(r+ x0). Силы отталкивания между частицами меняются с расстоянием быстрее , чем силы притяжения : R(r-x0)> R(r+ x0).
Под действием преобладающей силы отталкивания атом удаляется от соседнего атома на большее расстояние , чем приближается к нему. Таким образом, предположение о равенстве отклонений необходимо заменить неравенством :
А ( + ) > А ( - ),
где А ( - ) - максимальное удаление ; А ( + ) - максимальное сближение.
Колебания ионов в узлах происходят ангармонично (т.е. не по гармоничному закону), и расстояние между атомами с ростом температуры растет. Тело расширяется.
Из графика зависимости потенциальной энергии W от расстояния между частицами тоже можно прийти к выводу о тепловом расширении твердых тел. На рис.2 изображен график зависимости потенциальной энергии от расстояния между атомами в узлах кристаллической решетки.
|
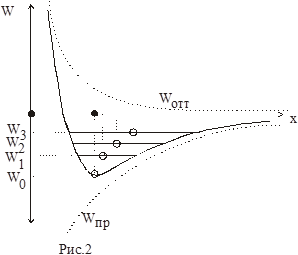
Кривая W несимметрична относительно минимума. По этой причине только малые колебания частиц около положения равновесия будут иметь гармонический характер. С ростом температуры растет кинетическая энергия колебаний частиц, за счет этого увеличивается полная энергия частиц ,
W0 = Wmin , W1 > W0 , W2 > W1 ,
Горизонтальными линиями внутри потенциальной ямы на рис.2 отмечена полная энергия колеблющихся частиц. Полная энергия при данной температуре сохраняется неизменной. При колебаниях кинетическая энергия имеет наибольшее значение в среднем положении. Она становится равной нулю в крайних точках ( точки пересечения прямой, соответствующей полной энергии, с графиком потенциальной энергии ) , так как полностью преобразуется в потенциальную. Частица , как маятник , в крайних положениях меняет направление движения , останавливаясь на мгновение в этих точках. Средние положения частицы В , отмеченные на рис.2 кружочком , с ростом температуры смещаются в сторону больших x , тело расширяется.
Описание установки
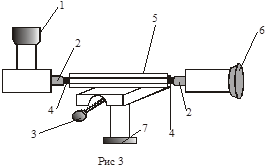
Установка для определения коэффициента линейного расширения состоит из термостата и оптиметра.
С помощью термостата достигаются заданные температурные условия для испытуемого образца. Инструкция к пользованию установкой для контроля, поддержания и регулирования температуры укреплена на приборе. Температура образца поддерживается постоянной следующим образом. С помощью термопары и электронного потенциометра производится изменение температуры. При достижении заданной температуры, установленной задатчиком, нагреватель отключается, при понижении температуры ниже заданной , нагреватель включается. Таким образом, температура образца поддерживается постоянной.
Горизонтальный оптиметр служит для непосредственного измерения с точностью до 0,001 мм удлинения образца , который нахо-
находится внутри нагревателя 4 (рис.3). Плоские концы образца должны слегка упираться в наконечники 2. Точная и тщательная установка образца производится после измерения его длины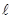 
при комнатной температуре с помощью штангенциркуля.
|
Порядок работы
Предлагается определить a для железа и алюминия.
1. Измерить начальную длину стержня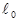 
штангенциркулем , занести в таблицу.
2. В нагреватель 5 вложить образец ; с помощью ручки 7 поднять столик до упора и повернуть его с помощью ручки 3. Затем, действуя в обратном порядке, поместить образец между наконечниками 2.
3. Наблюдая в окуляр 1, совместить нулевое деление шкалы с неподвижным указателем путем вращения ручки 6 – это показание оптиметра при t1 , т.е. при комнатной температуре.
4. Выставить задатчиком на электронном потенциометре заданную температуру t2 , включить установку в сеть. Образец начинает расширяться и шкала двигается. Когда температура образца достигнет заданной , расширение прекратится и шкала остановится. Наблюдают в окуляр , какое деление шкалы стоит против неподвижного указателя - это будет показание оптиметра при t2.
Все данные заносят в таблицу и по формуле вычисляют a:
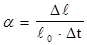
где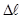 
есть разность показаний оптиметра при t2 и t1 ;
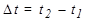
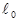- начальная длина стержня
5. Второй опыт проводят аналогично первому , т.е. совмещают нулевое деление шкалы с указателем при температуре t2, выставляют на потенциометре другую заданную температуру t 3, ждут когда шкала перестанет двигаться и снимают показание оптиметра при t3.
Данные заносят в таблицу , вычисляют второе значение a по формуле ( 1 ) , где 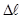- разность показаний оптиметра при t3 и t2 , умноженное на 0,001 ,
Dt = t3 - t2,
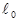- начальная длина стержня
6. Вычислить значение a по результатам обоих опытов.
7. Повторить опыты для другого образца.
Для установки начального положения используют микрометрический винт 6.
Образец укрепляется между наконечниками так, чтобы в трубку оптиметра 1 был виден правый край шкалы с делениями (стрелку оптиметра в начальный момент устанавливают винтом 6 в положение -80 или -90 мкм).
Контрольные вопросы
1. Объясните причины теплового расширения тел.
2. Коэффициент теплового расширения и его физический смысл.
3. Изобразите и объясните график зависимости потенциальной энергии от расстояния между атомами.
4. Расскажите об экспериментальной установке и ходе выполнения работы.
5. Сравните полученные данные с табличными.
| Показание оптиметра при t1 | Показание оптиметра при t2 | Удлинение Dl | t1 | t2 | разность температур Dt | a | Da | |
| Fe | ||||||||
| Al |
Литература
1. Яворский и др. Курс физики , т.1, 1983
2. Савельев И.В. Курс общей физики , т.1, 1977
3. Зисман и Тодес , Курс общей физики , т.1, 1974