Изотермический процесс

Дата: 2025-05-25; Просмотры: 4
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

 

При этом процессе температура остается постоянной (Т=const) В этом случае dT=0 и внутренняя энергия не изменяется dU=0 dQ = dA , т.е. вся подводимая теплота расходуется газом на совершение работы против внешних сил.

 

Изохорический процесс

 

При изохорическом процессе V=const, dV=0 и dA=0. Т.е. при этом процессе работа не совершается, т.к. объем не изменяется. Тогда 1 начало запишется:

 

dQ = dU .

 

Т.е. количество теплоты расходуется на изменение внутренней энергии. Но по определению 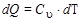(для 1 моля). Следовательно, .

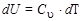Из этой формулы видно, что изменение внутренней энергии газа определяется только изменением его температуры. Теплоемкость при постоянном объеме (изохорная теплоемкость) равна:

 

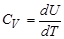
Изобарический процесс

В этом процессе изменяются и внутренняя энергия и работа против внешних сил:

,

 

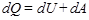т.е. теплота, подводимая к системе, идет на увеличение внутренней энергии и на совершение работы против внешних сил.

Для 1 моля газа уравнение Менделеева-Клапейрона

 

pV = RT ; pdV = RdT ,

 

но pdV = dA , поэтому dA = RdT , тогда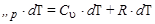

(Напомним, что С u и Cp - мольные теплоемкости)

 

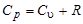, (12)

 

R - универсальная газовая постоянная равная работе расширения одного моля газа при нагревании на один градус в изобарическом процессе.

Уравнение (12) называется уравнением Роберта Майера. Из него следует: при изобарном нагревании 1 моля газа на 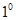часть теплоты, равная 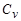, идет на увеличение внутренней энергии, а другая часть, равная R , - на совершение работы против внешних сил.

 

Адиабатический процесс

 

Так как при адиабатическом процессе dQ=0, то dA =- dU. Первое начало термодинамики будет иметь вид

 

dU + dA=0 или С V dT + PdV=0

 

Откуда следует, что при адиабатическом процессе работа совершается за счет изменения внутренней энергии.

Например, если открыть ниппель у автомобильного колеса, то выходящий воздух можно рассматривать как адиабатическое расширение. Работа по расширению воздуха происходит за счет уменьшения внутренней энергии, что приведет к охлаждению воздуха и ниппель станет холодным.

 

Степени свободы

 

Согласно молекулярно-кинетической теории внутренняя энергия, которая обусловлена движением молекул как поступательным так и вращательным, определяется (6), где i- число степеней свободы

Числом степеней свободы i называется число независимых координат, полностью определяющих положение молекулы в пространстве.

В случае жесткой связи например:

1. У одноатомной молекулы только три степени свободы поступательного движения, i=3 (для атома как материальной точки не учитывается вращательное движение); (рис.1).

2. У двухатомной молекулы три степени свободы поступательного движения и две степени свободы вращательного движения, i=5 (рис.2);

 

 

 


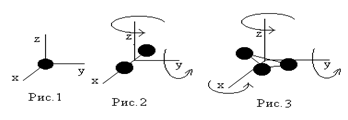3. У трехатомной молекулы три степени свободы поступательного движения и три степени свободы вращательного движения; i=6 (рис. 3).

Из (6) и (8) можно вычислить внутреннюю энергию и теплоемкости газа, а по формуле (1) определить адиабатическую постоянную g.

1. Для одноатомного газа i=3

 

;

;

.

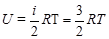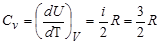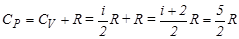Адиабатическая постоянная .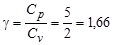

2. Для двухатомного газа i=5 и аналогично предыдущему получим

 

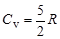
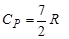
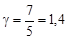
3. Для трехатомного газа i=6

 

;

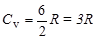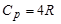
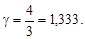
В общем случае:

; ; .

 

 

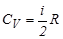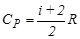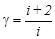4.Теория метода и описание установки

 

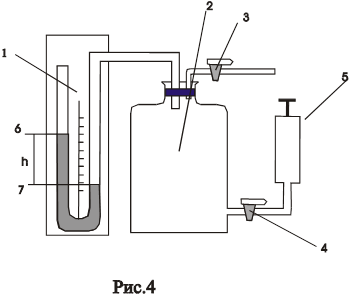
Рис.4.

 

Рис.5.

Экспериментальная установка состоит из стеклянного баллона 2 (рис.4), соединенного с манометром 1 и насосом 5. Посредством крана 3 баллон 2 может быть соединен с атмосферой. Давление в манометре h определяется по разности уровней жидкости левого колена 6 и правого колена 7. Для накачки воздуха в баллон надо открыть кран 4 и закрыть кран 3.Если при помощи насоса накачать в баллон некоторое количество воздуха, а затем закрыть кран 4, то давление и температура воздуха внутри баллона повысятся(внешними силами совершается работа по сжатию газа). Выждав определенное время (2-3 мин), вследствие теплообмена воздуха с окружающей средой температура воздуха, находящегося в баллоне, сравняется с комнатной температурой 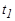, а давление при этом слегка понизится, о чем можно судить по показанию манометра.

Давление, установившееся в баллоне,

 

,

 

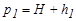где Н - атмосферное давление, 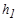-атмосферное давление, измеряемое разностью уровней жидкости в манометре 1.

Таким образом, состояние воздуха внутри баллона, которое назовем первым состоянием, будет характеризоваться параметрами: 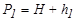; V ;Т1. Этому состоянию газа соответствует точка 1 рис.5. Затем открываем на короткое время кран 3 (рис.4), соединяем баллон с окружающей средой. Этот процесс расширения можно считать адиабатическим.

Давление в сосуде установится равным атмосферному P 2 = Н , температура понизится до Т2<Т1, а объем будет равен 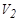. Следовательно, в конце адиабатического процесса у воздуха в баллоне будут параметры H ; V 2 ; T 2(T 2 < T 1) (рис.5 точка 2).

 

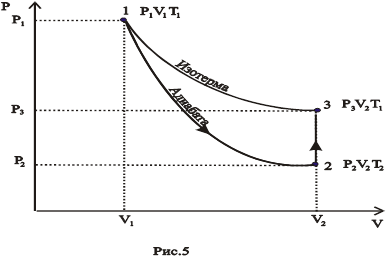
Переход из первого состояния во второе является адиабатическим, к такому переходу применим уравнение Пуассона

 

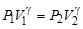. (13)

 

Через три-четыре минуты после закрытия клапана воздух в баллоне нагреется изохорически до комнатной температуры t 1 , а давление повышается до Р3 = H+ h 2(точка 3 на рис.5) h 2-разность уровней в манометре, когда температура в баллоне стала равной комнатной. Сравнивая конечное состояние «3» с первоначальным состоянием «1», видим, что они принадлежат одной и той же изотерме.

 

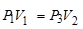(14)

 

Возведем (14) в степень g, получим 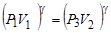и разделим его на (13): 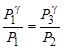прологарифмируем - 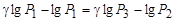, отсюда 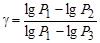. Принимая во внимание, что Р1= H + h 1 , P 2 = H , P 3 = H + h 2, т.е. давления мало отличаются друг от друга, разность логарифмов можно принять пропорциональными разностям самих давлений и

 

,

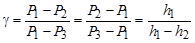откуда

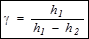. (15)

 

Последняя формула есть рабочая.

Порядок выполнения работы

1. Осторожно ( чтобы не выплеснуть жидкость из манометра ) накачайте в баллон воздух, так чтобы разность уровней в коленах манометра составляла 80-100 мм. Так как при нагнетании воздуха в баллон температура его возрастает ,то перед тем как снять показание давления, надо выждать одну минуту, пока через стенки баллона температура воздуха в нем не выравняется с температурой окружающей среды. Процесс выравнивания температуры можно заметить по небольшому изменению уровней жидкости в коленах манометра, которое прекращается, как только произойдет выравнивание температур. В это время снимите значение 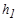, равное разности уровней.

2. Проведите над газом процесс адиабатического расширения (помните, что он должен пройти без теплообмена с окружающей средой ). Для этого откройте кран 3, при этом слышится характерное шипение. Как только оно прекратится, кран следует быстро закрыть. Расширяясь воздух в сосуде охладится .

3.Предоставьте возможность газу в баллоне через стенки нагреться до температуры окружающей среды, т.е. до первоначальной температуры 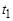. При нагревании газа давление в баллоне повышается, и уровень жидкости в коленах манометра изменяется. После выравнивания температуры снимите значение .

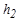4. Подставьте в рабочую формулу значения h 1 и h 2 вычислите значение g.Опыт повторите 5 - 7 раз.

Все полученные опытом и вычисленные результаты сводят в таблицу.

 

№ опыта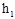
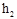
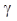
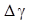
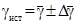
1
2
3
средние значения