Метод обработки опытных данных
И.С. Иванов, А.М. Светляков
Предположим, что в результате серии экспериментов получена таблица некоторой зависимости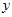 
от 
:
|
| 
| 
| …. | 
|
|
| 
| 
| … | 
|
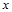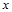
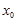
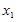
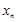
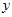
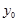
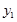
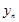
Надо найти формулу, выражающую эту зависимость аналитически
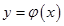(4.1)
Строгая функциональная зависимость для экспериментально полученной таблицы наблюдается редко, т.к. каждая из величин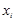 
и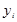 
может зависеть от многих случайных факторов. Однако если удастся найти 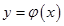, то во-первых, она позволит найти значение для не табличных значений 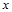, «сглаживая» результаты измерений величины 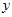, во-вторых, позволит экстраполировать функциональную зависимость, т.е. найти 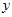, который соответствует некоторому 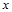, лежащему вне области эксперимента.
Задача: найти зависимость 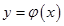, значения которой в точках 
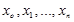мало отличается от опытных данных. Эта зависимость, полученная на основе опытных данных, называется эмпирической[1]. Задача построения эмпирической формулы отличается от задачи интерполирования. График эмпирической зависимости не проходит через заданные точки 
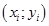, как в случае интерполяции. Это приводит к тому, что экспериментальные данные в некоторой степени «сглаживаются», а интерполяционная формула повторяла бы все ошибки, имеющиеся в данных. Построение эмпирической формулы состоит из двух этапов:
1) побора общего вида этой формулы,
2) определение наилучших значений, содержащихся в ней параметров.
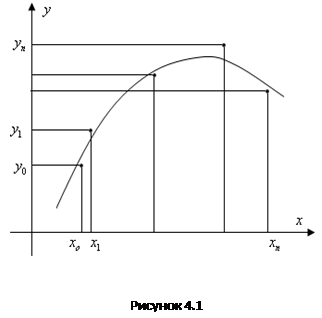
Для выполнения первого этапа строится по таблице точечный график, затем проводится плавная кривая, по возможности наилучшим образом отражающая характер расположения точек (см. рис. 4.1). По полученной таким образом кривой устанавливается вид приближающей функции.
Будем считать, что вид эмпирической формулы выбран:
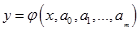, (4.2)
где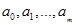 
– неизвестные постоянные параметры.
Обозначим разность между опытными данными и значениями эмпирической функции в точках 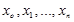через:
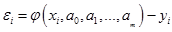, (4.3)
где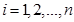 
.
Теперь задача нахождения параметров 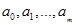сводится к минимизации отклонений 
.
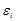Итак, согласно методу наименьших квадратов, параметры функции 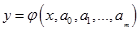надо выбирать таким образом, чтобы сумма квадратов отклонений 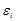была наименьшей.
Определим функцию:
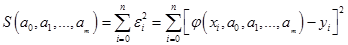, (4.4)
теперь задача сводится к отысканию ее минимума. Здесь 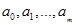выступают в роли независимых переменных функции 
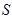. Минимум найдем приравнивая нулю частные производные по этим переменным: 
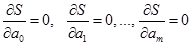, получим систему уравнений для определения .
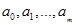Рассмотрим метод наименьших квадратов для частного случая, широко используемого на практике. В качестве эмпирической функции рассмотрим многочлен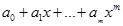 
, тогда 
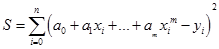. Найдем частные производные:
.
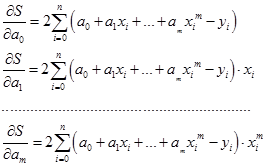Приравнивая их к нулю и собирая коэффициенты при неизвестных 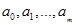, получим систему линейных уравнений:
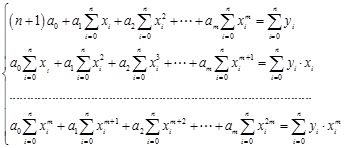(4.5)
Решая эту систему относительно неизвестных параметров 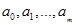, получим конкретный вид искомой функции .
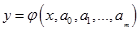Метод наименьших квадратов можно применять и к другим функциональным зависимостям, а не только к многочленам.
ЛИТЕРАТУРА
1. Заварыкин, В.М. Численные методы: учеб. пособие для студентов физ.-мат. спец. пед. ин-тов / В.М. Заварыкин, В.Г. Житомирский, М.П. Лапчик. – М.: Просвещение, 1990. – 176 с.
2. Бахвалов, Н.С. Численные методы / Н.С. Бахвалов. – М.: Наука, 1973.
3. Демидович, Б.П. Основы вычислительной математики / Б.П. Демидович, И.А. Марон. – М.: Наука, 1970.
4. Иванова, Т.П. Программирование и вычислительная математика / Т.П. Иванова, Г.В. Пухова. – М.: Просвещение, 1978.
5. Березин, И.С. Методы вычислений / И.С. Березин, Н. П. Жидков. – М.: Физматгиз, 1992.
6. Калиткин, Н.Н. Численные методы / Н.Н. Калиткин. – М.: Наука, 1978. – 512 с.
7. Мак-Кракен, Д. Численные методы / Д. Мак-Кракен, У. Дорн. – М.: Мир, 1997. – 584 с.
2 Методические указания к выполнению работы
Для создания и редактирования формул следует использовать редактор формул
Microsoft Equation. На стандартной панели Вставка в группе Текст есть кнопка Объект. Щелчок по этой кнопке открывает диалоговое окно Вставка объекта. Из предлагаемого списка надо выбрать название редактора формул - Microsoft Equation. После этих действий появляется окно редактора Microsoft Equation и панель инструментов Формула. Буквы и цифры, входящие в формулу, и некоторые часто используемые символы набираются с клавиатуры. Специальные символы и шаблоны вводятся с помощью панели инструментов Формула. Для выхода из редактора формул в документе Word нужно просто щелкнуть мышью вне окна редактора формул.
Графический объект расположите в нужном месте страницы, сгруппируйте его и выберите тип обтекания графического объекта текстом документа. Для этого выделите графический объект, при этом появятся контекстные инструменты Работа с рисунком, перейдите на контекстную вкладку Формат, далее – в группу Упорядочить, щелкните по кнопке Обтекание текстом и выберите нужную команду.
Чтобы сделать сноску в тексте документа, надо перейти на стандартную вкладку Ссылки, в группу Сноски. Установите курсор в то место документа, где должен стоять указатель сноски, и щелкните по кнопке Вставить сноску. Перенумерация сносок в документе выполняется автоматически.
Преподаватель __________ Ю.Г. Гетманова
[1] от от греч. empeiria – опыт