Регрессией называется функция , описывающая зависимость условного математического ожидания зависимой переменной от заданных фиксированных значений независимых переменных , где - объем выборки.
В общем случае, для описания функции регрессии необходимо знание условного закона распределения зависимой переменной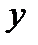 
. В практике экономического анализа такой информацией обычно не располагают, поэтому ограничиваются поиском подходящих аппроксимаций для распределений, основанных на исходных данных генеральной совокупности или данных выборки. При этом под аппроксимацией функций (от лат. approximato – приближение) понимают приближенное выражение одних функций другими. Задача аппроксимации возникает, например, при замене сложной функций простой, когда требуется вычислить значение данной функции.
Уравнение регрессии показывает, как в среднем изменяется переменная 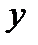при изменении любого из независимых переменных 
:
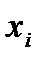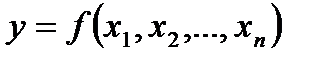. (2.55)
При этом зависимая переменная 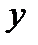всегда одна, а независимых переменных (факторов) 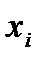может быть несколько. Если независимая переменная одна ( 
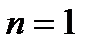), то имеет место простой регрессионный анализ. Если же независимых переменных несколько ( 
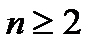), то имеет место многофакторный регрессионный анализ.
В практике экономического анализа наибольшее применение получили уравнения парной регрессии, отражающие взаимосвязь одного результативного признака с одним фактором, и уравнения множественной регрессии, отражающие взаимосвязь одного результативного признака с несколькими факторами. Для целей регрессионного анализа чаще всего используются следующие парные и множественные зависимости:
- парная линейная регрессия:
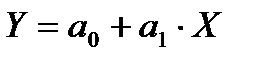; (2.56)
- парная параболическая регрессия:
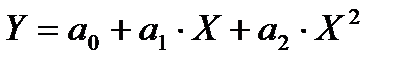; (2.57)
- парная полиномиальная регрессия степени p:
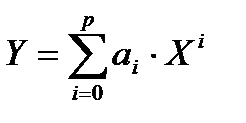; (2.58)
- парная гиперболическая регрессия:
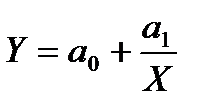; (2.59)
- парная степенная регрессия:
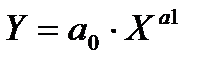; (2.60)
- парная показательная регрессия:
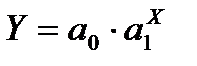; (2.61)
- множественная линейная регрессия:
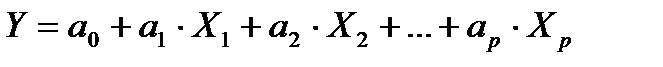; (2.62)
- множественная степенная регрессия:
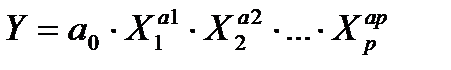. (2.63)
Посредством регрессионного анализа экономических явлений решаются две основные задачи:
- Построение уравнения регрессии, т.е. нахождение вида зависимости между результативным показателем 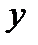и независимыми факторами
.
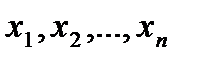2. Оценка значимости полученного уравнения регрессии, т.е. определение того, насколько выбранные факторные признаки 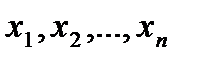объясняют вариацию признака .
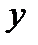Построение уравнения регрессии осуществляется, как правило, методом наименьших квадратов, сущность которого состоит в минимизации суммы квадратов отклонений фактических значений результативного признака от его расчетных значений по уравнению регрессии:
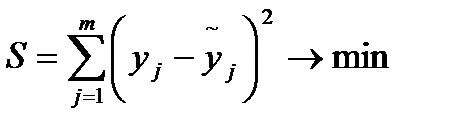, (2.64)
где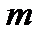 
- число наблюдений;
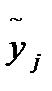- расчетное значение результативного фактора.
Кластерный анализ (от англ. cluster – группа) является одним из методов многомерного анализа, предназначенный для группировки (кластеризации) совокупности данных, элементы которой характеризуются многими признаками. Значения каждого их таких признаков служат координатами каждой единицы изучаемой совокупности в многомерном пространстве признаков. Каждое наблюдение, характеризующееся значениями нескольких показателей, можно представить как точку в пространстве этих показателей, значения которых рассматриваются как координаты в многомерном пространстве. Так, в многомерном пространстве указанных показателей расстояние между точками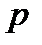 
и 
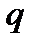внутри кластера с 
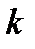координатами определяется следующим образом:
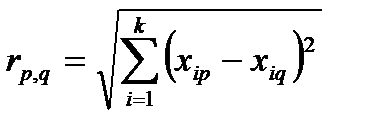. (2.65)
Основным критерием кластеризации является положение, согласно которому различия между кластерами должны быть более существенными, чем различия между наблюдениями, отнесенными к одному кластеру. Следовательно, в многомерном пространстве показателей должно выполняться неравенство
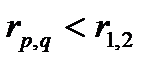, (2.66)
где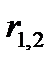 
- расстояние между кластерами 1 и 2 в многомерном пространстве показателей.
Как и многие расчетные процедуры регрессионного анализа, процедура кластеризации также достаточно трудоемка, поэтому ее целесообразно выполнять на компьютере, используя специальные программы.
Дисперсионный анализ представляет собой статистические метод, позволяющий подтвердить или опровергнуть гипотезу о том, что две выборки данных относятся к одной генеральной совокупности. Применительно к экономическому анализу можно сказать, что дисперсионный анализ позволяет определить, относятся ли группы разных наблюдений к одной и той же совокупности данных или нет.
Статистической гипотезой называется предположение о свойстве генеральной совокупности данных, которое можно проверить, опираясь на выборку данных. Гипотезы о параметрах генеральной совокупности называются параметрическими, а гипотезы о распределениях – непараметрическими. Гипотеза о том, что две совокупности, сравниваемые по одному или нескольким признакам, не отличаются, называются нулевой гипотезой (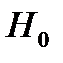 
).
Нулевая гипотеза отвергается тогда, когда по выборке получается результат, который при истинности выдвинутой нулевой гипотезы маловероятен. Границей невозможного или маловероятного обычно считают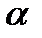 
= 0,05 (5%) или 0,01 (1%), 0,001 (0,1%). Для этого уровня вероятностей значения критериев рассчитаны в статистико-математических таблицах.
Дисперсионный анализ часто используется совместно с методами группировки данных. Задача анализа в таких случаях сводится к оценке существенности различий между группами наблюдений. Для этого определяются групповые дисперси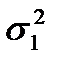и 
и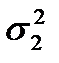 
, а затем по статистическим критериям Стьюдента ( 
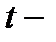критерий) или Фишера ( 
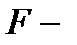критерий) проверяется значимость различий между группами наблюдений.
Собственно дисперсия характеризует меру рассеивания некоторой случайной величины 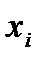, квадрат ее среднеквадратического отклонения.
Проверка гипотезы о средних величинах. Основными гипотезами о средних величинах являются:
- гипотеза о значении генеральной средней (при известной генеральной дисперсии или при неизвестной генеральной дисперсии);
- гипотезы о равенстве генеральных средних нормально распределенных совокупностей (при известных генеральных дисперсиях, при неизвестных равных генеральных дисперсиях, при неизвестных неравных генеральных дисперсиях).
Из этих двух первая задача, чаще всего, решается при неизвестной генеральной дисперсии. При этом испытуемая гипотеза :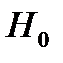 
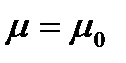, альтернативная гипотеза 
: 
( 
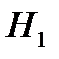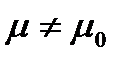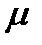и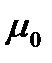 
, соответственно, характеристики генеральной совокупности и исследуемой выборки данных). Испытание гипотезы проводят с помощью 
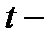критерия. При большом числе наблюдений критическое значение этого критерия определяется по таблице интеграла вероятностей 
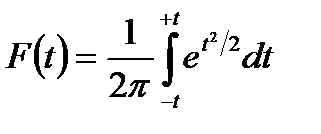, а при малом числе наблюдений – по таблице распределения Стьюдента с заданным уровнем значимости и числом степеней свободы 
.
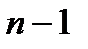Гипотеза 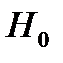не отклоняется в случае, если
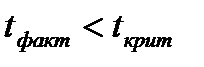. (2.67)
Гипотеза 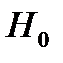отклоняется в случае, если
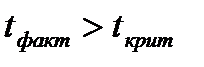. (2.68)
Если различие между фактическим и табличным (критическим) значением 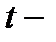критерия невелико, то вывод об отклонении (или не отклонении) гипотезы не считается достаточно надежным. И надежность такого вывода еще более понижается, если нет уверенности в нормальном распределении генеральной совокупности.
Если ставится задача сравнения двух и более выборочных дисперсий, то для ее решения применяется 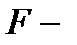критерий Фишера, который представляет собой отношений выборочных дисперси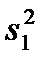й 
и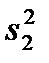 
как оценок одной и той же генеральной дисперсии 
:
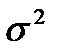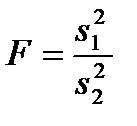. (2.69)
Испытуемая гипотеза является нулевой гипотезой :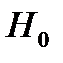 
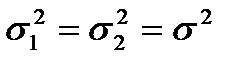, альтернативная гипотеза 
: 
.
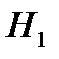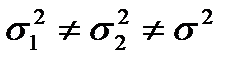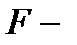критерий строится так, что в числителе стоит та дисперсия, которая больше. 
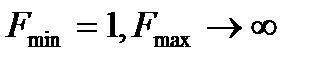. Критические значения критерия берутся из таблиц распределения, которое зависит от уровня значимости и от числа степеней свободы сравниваемых дисперсий.
Таким образом, в дисперсионном анализе общая вариация подразделяется на составляющие, и проводится сравнение этих составляющих. Испытуемая гипотеза заключается в том, что если данные каждой группы представляют случайную выборку из нормально распределенной генеральной совокупности, то величины всех частных дисперсий должны быть пропорциональны своим степеням свободы, и каждую их них можно рассматривать как оценку генеральной дисперсии.