В качестве показателей (характеристик) вариации чаще всего используются размах вариации, среднее линейное отклонение, среднеквадратическое отклонение, дисперсия, коэффициент вариации.
Размах вариации является одним из показателей вариации и характеризует пределы колеблемости (вариацию) индивидуальных значений признака (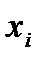 
) в совокупности. Размах вариации ( 
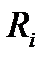) представляет собой разность между наибольшим ( 
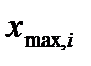) и наименьшим ( 
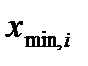) значениями i-го признака:
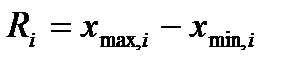. (2.42)
Среднее линейное отклонение (или средний модуль отклонения 
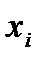) представляет собой отклонение значения признака ( ) от среднего арифметического ( 
) и вычисляется по формуле
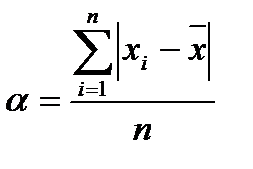. (2.43)
При использовании весовых коэффициентов (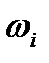 
) формула расчета средневзвешенного среднего линейного отклонения имеет вид
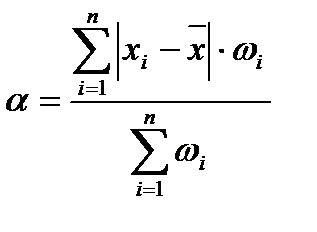, (2.44)
где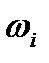 
- частота, с которой в изучаемой совокупности встречается значение признака .
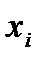Наиболее распространены при изучении вариации значений данных получили величины среднеквадратического отклонения и дисперсии.
Дисперсия представляет собой математическое ожидание квадрата отклонения случайной величины от ее математического ожидания. Дисперсией также называют средний квадрат отклонения значений признака от его среднего отклонения в генеральной совокупности. Чем больше величина дисперсии, тем сильнее разброс значений признака вокруг среднего. Расчет величины дисперсии (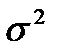 
) ведут как по формуле взвешенной дисперсии, так и по формуле невзвешенной дисперсии. Формула расчета невзвешенной дисперсии имеет вид
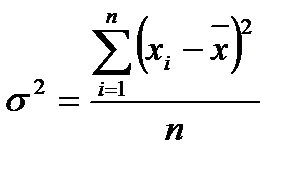, (2.45)
где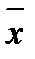 
- математическое ожидание случайной величины .
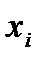В свою очередь, значение математического ожидания случайной величины можно определить по формуле
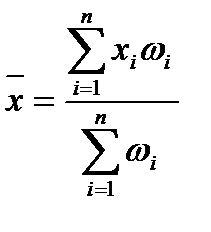. (2.46)
Формула расчета взвешенной дисперсии имеет такой вид:
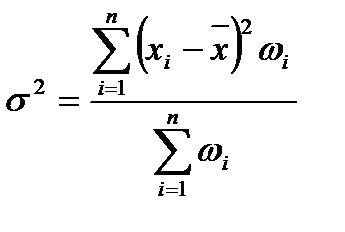. (2.47)
Среднеквадратическое отклонение ( 
) представляет собой корень второй степени из среднего квадрата отклонений значений признака от их средней величины (математического ожидания):
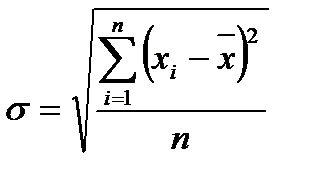; (2.48)
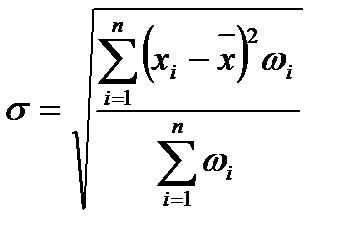; (2.49)
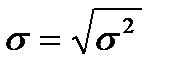. (2.50)
Чем больше величина или 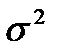, тем сильнее разброс значений ( 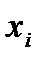) вокруг среднего. Следует отметить, что всегда больше модуля среднего линейного отклонения 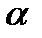. Так, для нормально распределенных величин имеет место соотношение
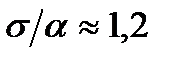. (2.51)
Если соотношение (2.51) не выполняется, то это свидетельствует о том, что в исследуемом массиве данных есть элементы, неоднородные с основной массой, т.е. сильно выбивающиеся по своей величине из общего ряда. В зависимости от решаемой задачи следует определить порядок исключения этих выбивающихся элементов из рассмотрения, либо не использовать их при построении некоторых моделей, поскольку эти элементы являются как бы исключениями из правила.
Как следует из определения величина среднеквадратического отклонения зависит от абсолютных значений изучаемого признака: чем больше величины 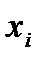, тем больше будет . Поэтому вводится показатель коэффициента вариации, чтобы сравнивать ряды данных, отличающихся по абсолютным величинам:
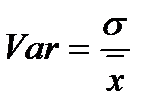. (2.52)
Коэффициент вариации является относительной мерой вариации и представляет собой отношение среднеквадратического отклонения ( ) к средней величине признака ( 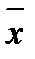). Коэффициент вариации является показателем количественной неоднородности исследуемой совокупности данных. При этом значение, равное 
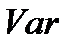=33% считается критическим. Если 
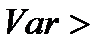33%, то исследуемую совокупность нельзя признать однородной. Чем меньше величина, тем меньше данные в совокупности отличаются друг от друга (тем меньше варианты признака отличаются один от другого по величине, тем однороднее исследуемая совокупность данных).
Таким образом, коэффициент вариации, будучи относительной величиной, абстрагирует различия абсолютных величин рядов данных и дает возможность их объективного сравнения.
Другими важнейшими аналитическими характеристиками вариационных рядов в системе стохастического моделирования являются асимметрия и крутизна распределения данных. Наряду с показателями общности и вариации они играют существенную роль в применении методов изучения связей.
Корреляционный анализ представляет собой метод установления связи различных данных исследования и измерения ее тесноты. Указанные данные можно считать случайными и выбранными из совокупности данных, имеющих нормальное многомерное распределение. Под корреляцией понимается зависимость между случайными величинами, не имеющая строго функционального характера, при которой изменение одной из случайных величин приводит к изменению математического ожидания (выборочной средней) другой случайной величины.
Основной задачей корреляционного анализа являются оценка параметров нормально распределенной многомерной совокупности (средние, дисперсия, парные коэффициенты корреляции), множественных и частных коэффициентов корреляции, проверка значимости оцениваемых параметров связи, выявление структуры взаимозависимых признаков. Дополнительной задачей корреляционного анализа считается построение различных (линейных) уравнений регрессии, статистические выводы относительно полученных уравнений и коэффициентов регрессии (принято объединять понятие корреляционно-регрессионного анализа).
Корреляционной связью называется такая статистическая связь, при которой различным значениям одной переменной (одного фактора) соответствуют разные значения другой переменной (другого фактора). Корреляционная связь может возникать несколькими путями, важнейшим из которых является причинная зависимость вариации результативного признака от изменения факторного признака. Кроме того, такой же вид связи может наблюдаться между двумя следствиями одной причины. Основной особенностью корреляционного анализа следует признать то, что он устанавливает лишь сам факт наличия какой-либо связи и степень ее тесноты, не вскрывая причин этой связи.
Если в статистике для определения тесноты корреляционной связи, как правило, применяются коэффициенты Фехнера, Пирсона, коэффициенты ассоциации и другие, то в системе экономического анализа деятельности хозяйствующих субъектов чаще используется линейный коэффициент корреляции.
Коэффициент корреляции (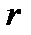 
) представляет собой числовую характеристику совместного распределения двух случайных величин или факторов ( 
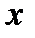и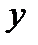 
), выражающую их взаимосвязь, и рассчитывается по следующим формулам:
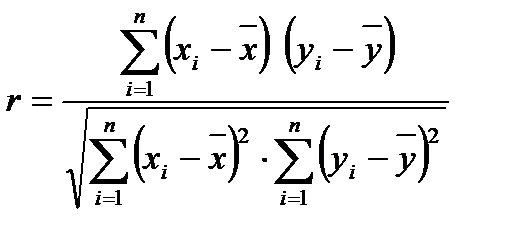; (2.53)
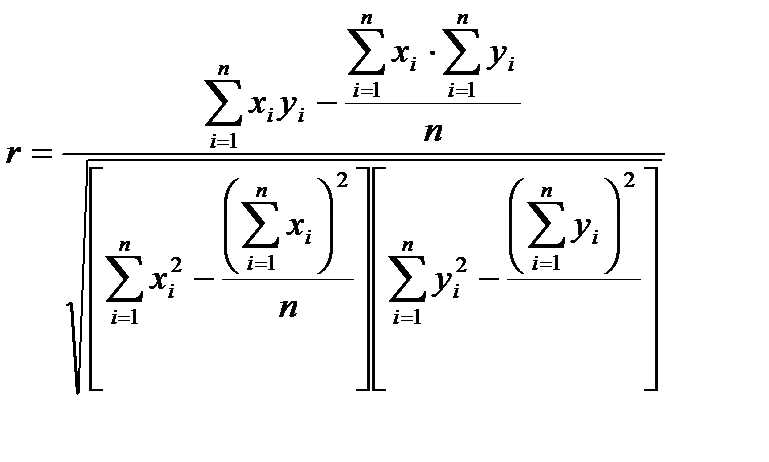. (2.54)
Таким же образом рассчитывается коэффициент корреляции между факторами в двухфакторной регрессионной модели вида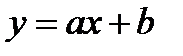 
, а также при любой другой связи между двумя показателями.
Значения коэффициента корреляции ( 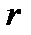) изменяются в интервале 
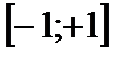. Значение 
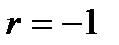свидетельствует о наличии жестко детерминированной обратно пропорциональной связи между факторами. Значение 
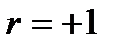соответствует жестко детерминированной связи между факторами с их прямо пропорциональной зависимостью. Значение 
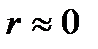говорит о том, что линейной связи между факторами не наблюдается. Другие значения коэффициента корреляции 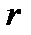свидетельствуют о наличии стохастической связи, причем, чем ближе абсолютное значение этого коэффициента 
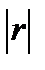к единице, тем теснее связь между факторами.
При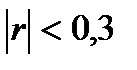 
связь считается слабой, при 
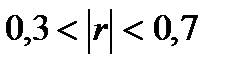имеет место связь среднего уровня тесноты, а при 
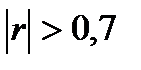связь считается тесной. На практике применяются и более дробные градации уровня 
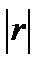, в частности, применяется таблица Чэддока.
Регрессионный анализ представляет собой метод установления аналитического выражения стохастической зависимости между исследуемыми признаками. Он направлен на исследование форм связи, устанавливающих количественное соотношение между случайными величинами (признаками) изучаемого случайного процесса. В этом смысле регрессионный анализ является частью корреляционного анализа.