Классические методы экономических исследований
Глава 2
АЛГОРИТМЫ И МЕТОДИКИ ИССЛЕДОВАНИЯ
СОСТОЯНИЯ И ПЕРСПЕКТИВ РАЗВИТИЯ
СОВРЕМЕННЫХ ЭКОНОМИЧЕСКИХ СИСТЕМ
2.1 Экономико-математическое моделирование.
Классические методы экономических исследований
Одним из наиболее важных направлений научных исследований экономических систем является использование экономико-математических методов, что позволяет сократить сроки проведения аналитических процедур, более полно выявить влияние факторов на результаты финансово-хозяйственной деятельности, заменить приближенные или упрощенные расчеты точными вычислениями, обеспечить постановку и выполнение новых многомерных задач анализа, которые практически невыполнимы вручную или традиционными способами.
Классификация экономико-математических методов исследования финансово-хозяйственной деятельности организаций может включать следующие группировки [4]:
- методы элементарной математики;
- классические методы математического анализа;
- методы математической статистики;
- эконометрические методы;
- методы математического программирования;
- методы исследования операций;
- методы экономической кибернетики;
- методы математической теории оптимальных процессов;
- эвристические методы.
Методы элементарной математики используются в обычных, традиционных экономических расчетах в целях обоснования потребностей в ресурсах, в учете затрат на производство и реализацию продукции (работ, услуг), расчете финансовых результатов деятельности, балансовых расчетах, разработке планов и проектов. Такие методы достаточно широко применяются в любой коммерческой организации.
Классические методы математического анализа выделены в отдельную группу, чтобы показать возможность их применения не только в рамках других методов (методов математической статистики, методов математического программирования и других), но и в качестве самостоятельной группы методов. К их числу относятся методы вариационного, дифференциального и интегрального исчисления. Так, факторный анализ показателей хозяйственной деятельности организации может быть осуществлен с применением методов дифференцирования и интегрирования.
Методы математической статистики применяются в тех случаях, когда изменение анализируемых показателей можно представить как случайный процесс. Эти методы являются основным средством изучения массовых, повторяющихся явлений и играют важную роль в прогнозировании показателей деятельности хозяйствующих субъектов. Если связь между анализируемыми характеристиками (показателями) не детерминированная, а стохастическая, то статистические и вероятностные методы считаются едва ли не единственным инструментом исследования. Из математико-статистических методов экономического анализа наибольшее распространение получили методы множественного и парного корреляционного анализа. К их числу также относятся методы изучения одномерных и многомерных статистических совокупностей.
Эконометрические методы анализа основаны на синтезе трех областей знаний – экономики, математики и статистики. В основе эконометрики лежит экономическая модель, являющаяся абстрактным отображением какого-либо экономического явления или процесса. Наибольшее распространение в современной экономике получил метод «затраты–выпуск», включающий матричные (балансовые) модели, построенные по шахматной схеме и позволяющие в наиболее компактной форме представить взаимосвязь затрат и результатов производства. Также достаточно широко используется метод производственной функции. Главными достоинствами матричных моделей экономического анализа являются удобство расчетов и четкость экономической интерпретации.
Методы математического программирования являются основным средством решения задач оптимизации хозяйственной деятельности в виде плановых расчетов. К числу этих методов относятся методы линейного и блочного программирования, метод нелинейного программирования (целочисленного, квадратического, параметрического программирования), метод динамического программирования. Ценность этих методов в системе экономического анализа заключается в оценке выполнения планов организации, напряженности плановых заданий, выявлении лимитирующих групп оборудования, видов сырья, материалов и полуфабрикатов, оценке дефицитности производственных ресурсов и т.п.
Методы исследования операций ориентированы на получение количественной оценки решений по разработке целенаправленных действий (операций) и выбор наилучшего из них. Целью такого исследования является оптимальное сочетание структурных взаимосвязанных элементов системы, которое в наибольшей степени отвечает критерию получения наилучшего экономического показателя. К числу этих методов относятся методы разработки линейных программ, управления запасами, оценки износа и замены оборудования, методы теории игр, теории расписания, сетевые методы планирования и управления, методы теории массового обслуживания. Методы теории игр предполагают использование математических моделей для принятия оптимальных решений в условиях неопределенности или конфликта нескольких сторон, имеющих существенно различающиеся интересы. Методами теории массового обслуживания исследуются процессы массового обслуживания, выводятся их количественные оценки на основе теории вероятностей.
Методами экономической кибернетики анализируют очень сложные экономические системы с точки зрения законов и механизмов управления и движения информации в них. К числу этих методов относятся методы системного анализа, методы моделирования, методы имитации (имитационного моделирования), методы обучения на основе деловых игр, методы распознавания образов. Наиболее распространены на практике методы моделирования и системного анализа.
Эвристические методы (решения) представляют собой неформализованные методы решения задач на основе интуиции, профессионального опыта и знаний, экспертных оценок специалистов и т.д.
В современной методологии экономико-математического моделирования выделяют две основные классификации методов и задач экономического анализа [4]:
· по классификационному признаку оптимальности все экономико-математические методы (задачи анализа) подразделяются на оптимизационные и неоптимизационные: если какой-либо метод (задача) позволяют найти решение по заданному критерию оптимальности, то он относятся к оптимизационным методам, если поиск решения ведется без критерия оптимальности, то используемый метод анализа относится к группе неоптимизационных методов;
· по признаку получения точного решения все экономико-математические методы подразделяются на точные и приближенные: если алгоритм метода позволяет получить единственное решение, то этот метод относится к точным методам, если при поиске решения используется стохастическая информация и решение можно получить с любой степенью точности, то используемый метод считается приближенным методом.
Экономический анализ, в широком смысле, представляет собой факторный анализ, под которым понимается постепенный переход от исходной факторной системы (исходная аналитическая информация) к конечной факторной системе (результативный показатель) с раскрытием полного набора прямых, количественно измеримых факторов, оказывающих влияние на изменения результативного показателя. Классификация методов факторного анализа представлена на рис. 2.1.
| МЕТОДЫ ФАКТОРНОГО АНАЛИЗА |
| Методы прямого факторного анализа |
| Методы обратного факторного анализа (синтез) |
| Пространственный анализ |
| Детерминированный анализ |
| Одноступенчатый анализ |
| Статический пространственный анализ |
| Оперативный анализ |
| Перспективный анализ |
| Цепной анализ |
| Динамический анализ |
| Стохастический анализ |
| Временной анализ |
| Ретроспективный анализ |
Рис. 2.1 – Укрупненная схема методов факторного анализа [4]
В случае применения методов прямого факторного анализа выявляются отдельные факторы, влияющие на изменение результативного показателя, устанавливаются формы детерминированной (функциональной) или стохастической зависимости между результативным показателем и определенным набором факторов, а также выясняется роль отдельных факторов в изменении результативного показателя. Постановка задачи прямого факторного анализа распространяется на детерминированный и стохастический случаи и может быть представлена в следующем виде.
Задается некоторая функция 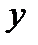 , характеризующая изменение какого-либо результативного показателя или экономического процесса:
, характеризующая изменение какого-либо результативного показателя или экономического процесса:
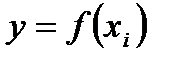 , (2.1)
, (2.1)
где 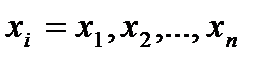 - набор влияющих факторов (рассматривается влияние
- набор влияющих факторов (рассматривается влияние 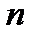 факторов).
факторов).
Таким образом, задана функциональная детерминированная форма связи изучаемого результативного показателя 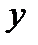 с набором факторов
с набором факторов 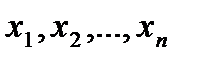 в следующем виде:
в следующем виде:
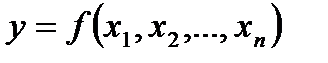 . (2.2)
. (2.2)
Постановка задачи прямого детерминированного факторного анализа при этом формулируется следующим образом: если показатель 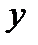 получил за анализируемый период некоторое приращение (
получил за анализируемый период некоторое приращение ( 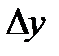 ), то требуется определить, какой частью изменение численного значения функции
), то требуется определить, какой частью изменение численного значения функции 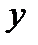 обязано приращению каждого аргумента (фактора)
обязано приращению каждого аргумента (фактора) 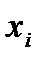 .
.
Примерами применения метода прямого детерминированного факторного анализа являются анализ влияния производительности труда и численности работающих на объем произведенной продукции (на объем проданных товаров, предоставленных услуг), анализ влияния величины прибыли, стоимости основных производственных фондов и оборотных средств на уровень рентабельности продукции и многие другие.
Постановка задачи прямого стохастического факторного анализа имеет свои особенности: в отличие от прямого детерминированного факторного анализа, когда исходные данные заданы в форме конкретных чисел, в случае применения прямого стохастического факторного анализа исходные данные задаются временной или поперечной выборкой. Поэтому здесь требуется глубокое экономическое исследование для выявления основных факторов, подбор вида регрессии, наилучшим образом отражающей связь исследуемого объекта с факторами, разработка метода определения влияния каждого фактора на результативный показатель.
Если результаты прямого детерминированного анализа должны получиться точными и однозначными, то результаты прямого стохастического анализа получаются с некоторой вероятностью (надежностью), которую еще следует оценить. Примером применения метода прямого стохастического факторного анализа может служить регрессионный анализ производительности труда, товарооборота и др.
Кроме задач, сводящихся к детализации показателя и разбивке его на составляющие части, в экономическом анализе существует ряд обратных задач, в которых требуется увязать ряд экономических характеристик в комплекс (т.е. построить функцию, содержащую основное качество всех показателей-аргументов). Такие обратные задачи, по существу, являются задачами синтеза.
Если некий экономический процесс 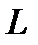 характеризуется набором показателей
характеризуется набором показателей 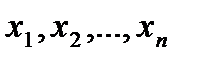 , каждый из которых односторонне характеризует процесс
, каждый из которых односторонне характеризует процесс 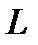 , и требуется построить функцию
, и требуется построить функцию 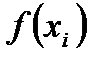 изменения процесса
изменения процесса 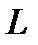 , содержащую основные характеристики вышеуказанных показателей в комплексе, то в зависимости от целей исследования эта функция
, содержащую основные характеристики вышеуказанных показателей в комплексе, то в зависимости от целей исследования эта функция 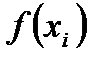 должна характеризовать процесс
должна характеризовать процесс 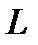 в статике или в динамике. Такая постановка задачи исследования предполагает использование метода обратного факторного анализа.
в статике или в динамике. Такая постановка задачи исследования предполагает использование метода обратного факторного анализа.
Методы обратного факторного анализа также подразделяются на детерминированные и стохастические. В качестве примеров использования методов обратного детерминированного факторного анализа можно привести комплексную оценку производственно-хозяйственной деятельности коммерческой организации, решение задач математического программирования. В качестве примеров использования методов обратного стохастического факторного анализа можно привести вычисления производственных функций, посредством которых устанавливаются зависимости между величиной выпуска продукции и затратами производственных ресурсов (первичных факторов).
В целях детального исследования экономических показателей, процессов, явлений возможно проведение не только одноступенчатого, но и цепного факторного анализа. К разновидностям цепного факторного анализа относятся статический (пространственный) факторный анализ и динамический (пространственный и временной) факторный анализ.
Так, в случае исследования поведения экономического показателя 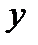 с влияющими на этот показатель факторами
с влияющими на этот показатель факторами 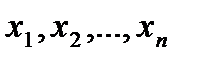 возможно применение одного из методов факторного анализа. Если перечисленные факторы
возможно применение одного из методов факторного анализа. Если перечисленные факторы 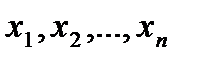 представляют собой функции некоторых первичных факторов, то для анализа следует объяснить поведение этих факторов. С этой целью проводят дальнейшую детализацию по такой схеме:
представляют собой функции некоторых первичных факторов, то для анализа следует объяснить поведение этих факторов. С этой целью проводят дальнейшую детализацию по такой схеме:
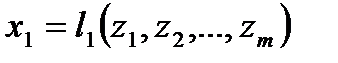 ; (2.3)
; (2.3)
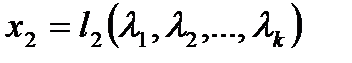 ; (2.4)
; (2.4)
………………………. ..…
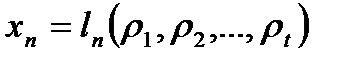 . (2.5)
. (2.5)
Детализация факторов, при необходимости, может быть продолжена и далее. Закончив ее, решают обратную задачу факторного анализа. При этом синтезируют результаты исследования для характеристики результативного показателя 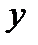 . Данный метод исследования называют цепным статическим методом факторного анализа. В случае применения цепного динамического метода факторного анализа для полного изучения поведения результативного показателя недостаточно знать его статическое значение, анализ показателя необходимо проводить на различных интервалах времени.
. Данный метод исследования называют цепным статическим методом факторного анализа. В случае применения цепного динамического метода факторного анализа для полного изучения поведения результативного показателя недостаточно знать его статическое значение, анализ показателя необходимо проводить на различных интервалах времени.
Задачей временного факторного анализа является изучение динамических временных рядов показателей хозяйственной деятельности, при этом производится расщепление уровня ряда на его составляющие:
· основную линию развития (тренд);
· сезонную или периодическую составляющую:
· циклическую составляющую, связанную с воспроизводственными процессами;
· случайную составляющую.
Экономико-математическое моделирование экономических систем и процессов является важным инструментом научных исследований. Содержание метода моделирования составляет конструирование модели, экспериментальный или теоретический анализ модели, сопоставление результатов с данными об объекте исследования, корректировки модели. Модель конструируется так, чтобы отобразить существенные характеристики исследуемого объекта (свойства, взаимосвязи, структурные и функциональные параметры и т.п.). Построенная экономико-математическая модель должна быть адекватной действительности, исследуемому объекту.
Построение (моделирование) конечной факторной системы для анализируемого показателя можно осуществить как формальным, так и эвристическим путем (на основе качественного анализа сущности экономического явления или процесса). Моделирование факторной системы основывается на следующих экономических критериях, обусловливающих выделение (отбор) факторов в качестве элементов факторной системы: причинность, достаточная специфичность, самостоятельность существования, учетная возможность.
Детерминированное моделирование факторных систем. В детерминированном моделировании факторных систем можно выделить типовые конечные факторные системы, наиболее часто встречающиеся в экономическом анализе деятельности организаций:
1. Аддитивные модели.
- Мультипликативные модели.
- Кратные модели.
При построении аддитивных моделей используется следующее аналитическое выражение:
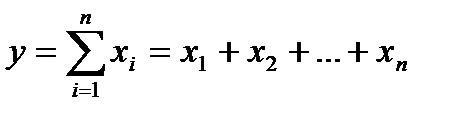 . (2.6)
. (2.6)
При построении мультипликативных моделей используется следующее аналитическое выражение:
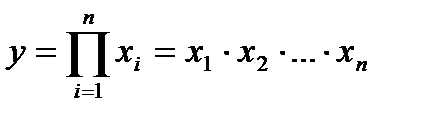 . (2.7)
. (2.7)
При построении кратных (смешанных) моделей используются следующие аналитические выражения:
 ; (2.8)
; (2.8)
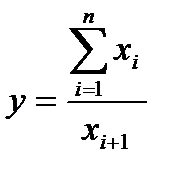 ; (2.9)
; (2.9)
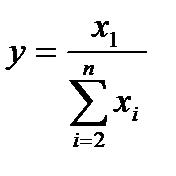 ; (2.10)
; (2.10)
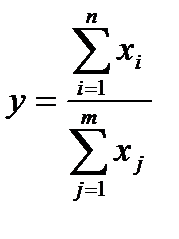 . (2.11)
. (2.11)
где 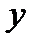 - результативный показатель (исходная факторная система);
- результативный показатель (исходная факторная система);
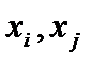 - факторы (факторные показатели).
- факторы (факторные показатели).
Применительно к классу детерминированных факторных систем используются следующие основные приемы и методы моделирования:
1. Метод удлинения факторной системы.
- Метод расширения факторной системы.
- Метод сокращения факторной системы.
При использовании метода удлинения факторной системы исходная факторная система имеет, например, следующий вид:
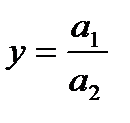 . (2.12)
. (2.12)
Если фактор 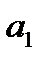 можно представить в виде суммы отдельных слагаемых (факторов):
можно представить в виде суммы отдельных слагаемых (факторов):
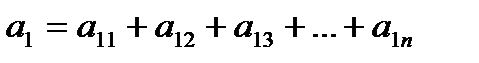 . (2.13)
. (2.13)
Следовательно, конечная факторная система будет иметь вид
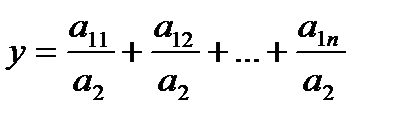 . (2.14)
. (2.14)
Таким образом, конечная факторная система, выраженная формулой (2.14), соответствует типовой аддитивной модели (2.6).
При использовании метода расширения факторной системы, если исходная факторная система имеет, например, вид (2.12), то при «расширении» и числителя, и знаменателя этой дроби умножением на одно и то же число (например, 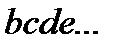 ), можно получить новую факторную систему следующего вида:
), можно получить новую факторную систему следующего вида:
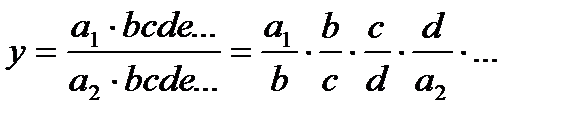 (2.15)
(2.15)
В этом случае конечная факторная система, выраженная формулой (2.15), соответствует типовой мультипликативной модели (2.7).
При использовании метода сокращения факторной системы, если исходная факторная система имеет, например, вид (2.12), то при «сокращении» и числителя, и знаменателя этой дроби путем их деления на одно и то же число (например, 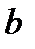 ), можно получить новую факторную систему (с безусловным соблюдением правила выделения факторов):
), можно получить новую факторную систему (с безусловным соблюдением правила выделения факторов):
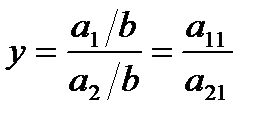 . (2.16)
. (2.16)
В этом случае конечная факторная система, выраженная формулой (2.16), также будет соответствовать типовой кратной модели (2.8).
В качестве промежуточных выводов можно указать, что детерминированное моделирование факторных систем представляет собой простое и эффективное средство формализации связи экономических показателей, которое служит основой для количественной оценки уровня влияния отдельных факторов на изменения экономического явления или процесса в динамике изменения обобщающего показателя хозяйственной деятельности. В основе детерминированного моделирования факторных систем лежит возможность тождественного преобразования исходной формулы экономического показателя по теоретически предполагаемым прямым связям этого показателя с другими показателями-факторами.
Вместе с тем, следует иметь в виду, что детерминированное моделирование факторных систем ограничено длиной факторного поля прямых связей. При недостаточном уровне знаний (представлений) о природе прямых связей того или иного показателя хозяйственной деятельности требуется иной подход к исследованиям. Размах (рассеяние) количественных изменений экономических показателей можно оценить только на основе стохастического анализа массива эмпирических данных.
Стохастическое моделирование факторных систем. Стохастический анализ направлен на исследование не прямых, а косвенных связей, на исследование опосредованных факторов (в случае невозможности определения непрерывной цепи прямой связи). С методологической точки зрения стохастическое моделирование факторных систем ориентировано на выявление взаимосвязей отдельных сторон хозяйственной деятельности и опирается на обобщение закономерностей варьирования значений экономических показателей (количественных характеристик факторов и результатов хозяйственной деятельности). При этом количественные параметры таких взаимосвязей выявляются на основе сопоставления различных значений изучаемых показателей, относящихся к определенному временному периоду или виду деятельности.
Таким образом, исходной первой предпосылкой стохастического моделирования является возможность формирования некоторой совокупности данных наблюдений (т.е. возможность повторно измерять параметры одного и того же экономического явления в различных условиях). В отличие от этого, в случае детерминированного факторного анализа модель изучаемого явления не изменяется во времени или при переходе от одного объекта исследования к другому.
Второй предпосылкой применимости стохастического моделирования факторных систем является качественная однородность совокупности данных относительно изучаемых взаимосвязей. Это обусловлено тем, что при необходимости сравнения результатов деятельности организации в различные периоды времени, должна быть обеспечена сопоставимость показателей. Третья предпосылка стохастического анализа сводится к требованию обеспечить достаточно большой объем совокупности данных наблюдений, который позволял бы с достаточной надежностью и точностью выявлять изучаемые закономерности, так как моделируемые взаимосвязи существуют в скрытом виде, они переплетаются со случайными компонентами вариации исследуемых показателей. Четвертая предпосылка требует наличия методов, позволяющих выявлять количественные параметры связей экономических показателей на основе массива данных варьирования уровня этих показателей.
Исходя из вышеизложенного, можно сделать еще один промежуточный вывод о том, что основная особенность стохастического факторного анализа заключается в том, что при стохастическом анализе модели не составляются путем качественного, теоретического анализа, для этого требуется количественный анализ эмпирических данных.
Классические методы экономических исследований. В группу классических методов экономического анализа обычно включают метод сравнения, балансовый метод, методы детерминированного факторного анализа (к ним относятся метод цепных подстановок, метод исчисления арифметических разниц, метод выявления изолированного влияния факторов, а также дифференциальный, интегральный и логарифмический методы), прогнозирование на основе пропорциональных зависимостей [4].
Метод сравнения является наиболее ранним и наиболее распространенным методом анализа. Сравнение начинается с сопоставления явлений или процессов и выделения в них общего и различного. В экономическом анализе метод сравнения считается одним из важнейших, с него, собственно, и начинается анализ. В практике экономического анализа выделяют несколько разновидностей метода сравнения:
· сравнение с планом (нормой, нормативом);
· сравнение с прошлым;
· сравнение с лучшим;
· сравнение со средними данными.
Необходимым условием корректного сравнения является сопоставимость объектов сравнения, их одинаковость по содержанию и структуре, по ценам, по структуре выпуска продукции и ее реализации и т.д. Для обеспечения сопоставимости показателей допускаются их корректировки (например, для корректного сравнения затрат, образованных при различных объемах производства и реализации продукции, необходимо привести эти затраты к какому-либо одному объему производства и реализации продукции). Выявленные в результате сравнения отклонения являются объектом дальнейшего анализа.
Важной задачей экономического анализа является сравнение фактических показателей с плановыми показателями деятельности хозяйствующего субъекта. В случае выявлении отклонений следует анализ факторов, обусловивших такие отклонения, а также устанавливаются обстоятельства, связанные с качеством самого планирования (нормирования).
Сравнение текущих показателей с прошлым, с показателями предыдущих периодов также широко применяется в экономическом анализе. Здесь важно обеспечить сопоставимость исследуемых показателей путем пересчета цен, ряда статей затрат с применением индексов цен, а также учесть влияние и других факторов (социальных, природных и т.д.).
Метод сравнения с лучшим предполагает сравнение показателей работы исследуемого объекта с лучшими показателями данного и других объектов, основанных на передовом опыте, достижениях науки и техники. Так, внутри предприятия могут сравниваться показатели лучших цехов, участков, бригад, отдельных работников. Существенное значение для целей анализа и управления имеет сравнение с показателями других предприятий, фирм, которые работают в аналогичных условиях (при этом особенно важна оценка и сравнение с зарубежным опытом работы).
Метод сравнения со средними показателями часто используется в анализе работы объединений, групп предприятий, концернов. Здесь не всегда допустимо простое сравнение, почти всегда имеются существенные отличия в работе различных предприятий. Целесообразно использовать для сравнения средние показатели, рассчитанные по производственным профилям деятельности, по однородным группам предприятий.
Балансовый метод. Балансовый метод, главным образом, предназначен для отображения соотношений, пропорций двух групп взаимосвязанных экономических показателей, итоги которых должны быть тождественными. Данный метод достаточно широко распространен в системе бухгалтерского учета, в планировании, иногда он используется также в экономическом анализе для исследования обеспеченности хозяйствующих субъектов материальными, трудовыми и финансовыми ресурсами, обеспеченности средствами производства и полноты их использования в хозяйственной деятельности. При оценке обеспеченности какого-либо предприятия ресурсами составляют баланс, в котором, с одной стороны, показывают потребность и их расход в данном виде ресурсов, а с другой стороны, показывают фактическое их наличие и поступление. Так, в системе анализа использования трудовых ресурсов предприятия сравнивается возможный (необходимый, требуемый) фонд рабочего времени с фактическим количеством отработанных часов, определяются причины сверхплановых (сверхнормативных) потерь рабочего времени. Для определения платежеспособности предприятия используется платежный баланс, в котором соотносятся наличие и поступление платежных средств с платежными обязательствами и расходом денежных средств.
В системе экономического анализа балансовый метод обычно используется как вспомогательное средство для проверки исходных данных и сведений, на основе которых далее проводится собственно экономический анализ, а также для проверки правильности аналитических расчетов.
Балансовый метод достаточно широко используется при построении детерминированных факторных моделей аддитивного типа. Например, на практике такие модели могут основываться на товарном балансе:
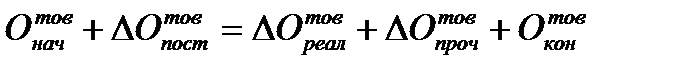 , (2.17)
, (2.17)
где 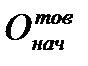 - остаток товаров на начало периода;
- остаток товаров на начало периода;
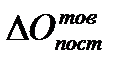 - поступление товаров в течение периода;
- поступление товаров в течение периода;
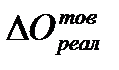 - продажа товаров в течение периода;
- продажа товаров в течение периода;
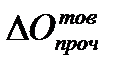 - другие направления расходования товаров в течение периода;
- другие направления расходования товаров в течение периода;
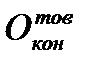 - остаток товаров на конец периода.
- остаток товаров на конец периода.
Метод цепных подстановок. Данный метод основан на элиминировании (устранении, отклонении, исключении) воздействия всех факторов на величину результативного показателя, кроме одного фактора. При этом исходят из того, что все факторы изменяются независимо друг от друга: сначала изменяется один фактор, а все остальные остаются без изменения, затем изменяются два фактора, затем три фактора и так далее при неизменности остальных факторов. Это позволяет определить влияние каждого фактора на величину исследуемого показателя в отдельности.
Этот метод относится к разновидностям детерминированного факторного анализа и состоит в последовательном рассмотрении влияния отдельных факторов на общий результат. При этом последовательно заменяются базисные (плановые) показатели фактическими показателями и новый результат сравнивается с прежним результатом. Данный метод применяется только в случае прямой пропорциональной или обратно пропорциональной зависимости между факторами и результативными показателями. Для правильного применения этого метода важна последовательность подстановки, что можно показать на примере, в котором определяется влияние трудовых факторов на объем производства промышленной продукции. Пусть зависимость объема производства продукции от трудовых факторов формализуется в виде выражения
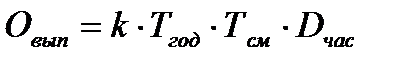 , (2.18)
, (2.18)
где 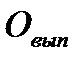 - объем выпуска продукции из производства;
- объем выпуска продукции из производства;
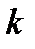 - среднесписочная численность рабочих;
- среднесписочная численность рабочих;
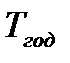 - среднее число смен, отработанных одним рабочим за год;
- среднее число смен, отработанных одним рабочим за год;
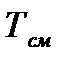 - среднее число часов, отработанных за одну смену;
- среднее число часов, отработанных за одну смену;
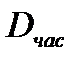 - средняя выработка продукции за один час в расчете на одного рабочего.
- средняя выработка продукции за один час в расчете на одного рабочего.
Из приведенной формулы видно, что объем выпуска продукции равен произведению четырех перечисленных выше показателей. Следовательно, необходимо сделать пять расчетов для измерения каждого из них. Исходные данные для указанных расчетов сводятся в табл. 2.1.
Таблица 2.1 – Исходные данные для определения влияния трудовых факторов
на показатель объема производства продукции
| Показатели деятельности промышленного предприятия | Плановые (базисные) | Фактические |
| Объем выпуска промышленной продукции, млн. руб. | 1482,9 | 1673,9 |
| Среднесписочная численность рабочих предприятия, чел. | 984 | 1017 |
| Среднее число смен, отработанных одним рабочим за год | 278 | 273 |
| Среднее число часов, отработанных одним рабочим за смену, час. | 7,8 | 7,7 |
| Средняя выработка промышленной продукции в расчете на один отработанный человеко-час, руб. | 695 | 783 |
Согласно данным представленной таблицы план выпуска промышленной продукции за анализируемый период был перевыполнен предприятием на (1673,9 – 1482,9) = 191,0 млн. руб. Для того, чтобы определить уровень влияния различных трудовых факторов на объем выпуска промышленной продукции, необходимо выполнить соответствующие расчеты.
Первый расчет. Проводится по формуле (2.18), причем все численные значения факторов, подставляемые в формулу, плановые:
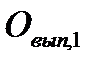 = 984 . 278 . 7,8 . 695 = 1482,9 млн. руб.
= 984 . 278 . 7,8 . 695 = 1482,9 млн. руб.
Второй расчет. Проводится по формуле (2.18), все численные значения трудовых факторов плановые, кроме значения фактора среднесписочной численности рабочих (подставляется его фактическое значение, равное 1017 чел.):
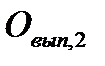 = 1017 . 278 . 7,8 . 695 = 1532,7 млн. руб.
= 1017 . 278 . 7,8 . 695 = 1532,7 млн. руб.
Третий расчет. Проводится по формуле (2.18), все численные значения факторов плановые, кроме значения фактора среднесписочной численности рабочих (подставляется его фактическое значение, равное 1017 чел.) и значения фактора среднего числа смен, отработанных одним рабочим за год (подставляется его фактическое значение, равное 273):
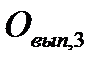 = 1017 . 273 . 7,8 . 695 = 1505,1 млн. руб.
= 1017 . 273 . 7,8 . 695 = 1505,1 млн. руб.
Четвертый расчет. Также проводится по формуле (2.18), в которую подставляются все фактические значения трудовых факторов, кроме значения фактора средней выработки промышленной продукции в расчете на один отработанный человеко-час (подставляется его плановое значение, равное 695 руб.):
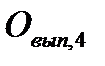 = 1017 . 273 . 7,7 . 695 = 1485,8 млн. руб.
= 1017 . 273 . 7,7 . 695 = 1485,8 млн. руб.
Пятый расчет. Проводится по формуле (2.18), в которую подставляются все фактические значения трудовых факторов:
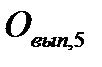 = 1017 . 273 . 7,7 . 783 = 1673,9 млн. руб.
= 1017 . 273 . 7,7 . 783 = 1673,9 млн. руб.
Полученные результаты вносятся в табл. 2.2.
Таблица 2.2 – Результаты оценки влияния трудовых факторов на повышение показателя
объема выпуска продукции методом цепных подстановок
| Трудовые факторы деятельности предприятия | Формула расчета | Уровень влияния фактора, млн. руб. |
| Увеличение среднесписочной численности рабочих | 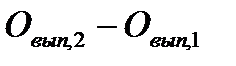
| 49,8 |
| Уменьшение числа смен, отработанных одним рабочим | 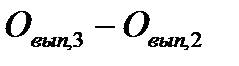
| -27,6 |
| Уменьшение среднего числа часов, отработанных одним рабочим за смену | 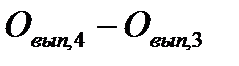
| -19,3 |
| Увеличение средней выработки продукции в расчете на один отработанный человеко-час | 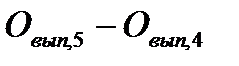
| 188,1 |
| Общее отклонение | 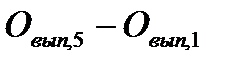
| 191,0 |
Анализ результатов, представленных в табл. 2.2, показывает, что два трудовых фактора оказывали положительное влияние на увеличение выпуска промышленной продукции, а два фактора – оказывали отрицательное влияние. Очевидно, отрицательное влияние на показатель выпуска продукции двух трудовых факторов было связано с целодневными и внутрисменными простоями, превысившими соответствующие плановые показатели. При условии решения организационной проблемы с простоями показатель выпуска промышленной продукции на предприятии может быть увеличен.
Следует иметь в виду, что при использовании метода цепных подстановок очень важно обеспечить строгую последовательность подстановки, так как ее произвольное изменение может привести к неправильным результатам. Произвольное изменение последовательности подстановки изменяет количественную весомость того или иного показателя.
Метод цепных подстановок в обобщенном виде имеет следующий алгоритм. Формула для определения базисного значения результирующего показателя имеет следующий вид:
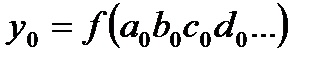 , (2.19)
, (2.19)
где 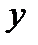 - результирующий показатель;
- результирующий показатель;
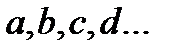 - факторы.
- факторы.
Формулы для определения промежуточных значений результирующего показателя имеют такой вид:
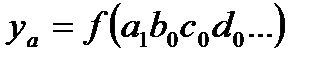 , (2.20)
, (2.20)
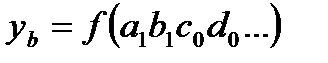 , (2.21)
, (2.21)
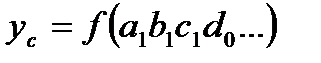 , (2.22)
, (2.22)
……………………..
Формула для определения фактического значения результирующего показателя имеет следующий вид:
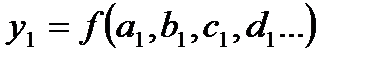 . (2.23)
. (2.23)
Общее абсолютное отклонение результирующего показателя ( 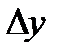 ) определяется по формуле
) определяется по формуле
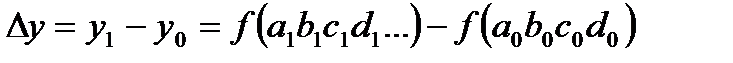 . (2.24)
. (2.24)
Далее общее отклонение результирующего показателя раскладывается по факторам. Так, отклонение результирующего показателя за счет действия фактора 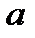 должно определяться по следующей формуле:
должно определяться по следующей формуле:
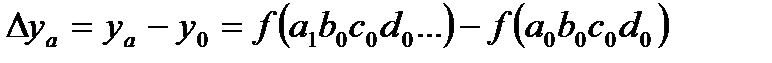 . (2.25)
. (2.25)
Отклонение результирующего показателя за счет действия фактора 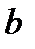 должно определяться по следующей формуле:
должно определяться по следующей формуле:
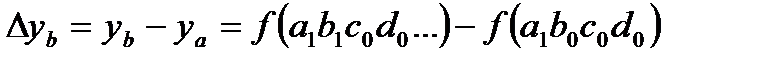 . (2.26)
. (2.26)
Отклонение результирующего показателя за счет действия фактора  должно определяться по следующей формуле:
должно определяться по следующей формуле:
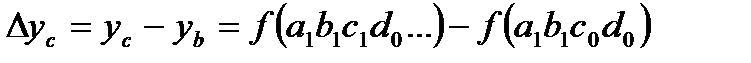 . (2.27)
. (2.27)
И так далее, по другим исследуемым факторам.
2.2 Возможности использования методов математической статистики
в системе экономических исследований
Метод группировок. Под группировкой понимают процесс образования групп единиц совокупности, однородных в каком-либо существенном отношении, а также имеющих одинаковые или близкие значения группировочного признака. Для осуществления группировки устанавливают признак, по которому единицы совокупности распределяют по группам, а также число групп и их обозначение (границы). Группировочный признак есть основание группировки, в зависимости от целей и задач исследования в качестве основания группировки может быть взят один или несколько признаков. Например, при группировке промышленных предприятий в качестве группировочного признака могут быть взяты объем выпущенной продукции, стоимость основных производственных фондов, численность работающих и другие. Выбор исследователем группировочного признака в значительной степени определяет результаты группировки и выводы, которые делаются на их основе [4].
Группировка показателей является неотъемлемой частью почти любого исследования, позволяя изучать экономические явления или процессы в их взаимосвязи и взаимозависимости. Метод группировки сводится к делению массива показателей изучаемой совокупности экономических объектов на качественно однородные группы по соответствующим признакам. Группировка всегда предполагает определенную классификацию явлений и процессов, а также причин и факторов, их обусловливающих, и должна быть научно обоснованной. Нельзя группировать явления или процессы, причины или факторы по случайным признакам, необходимо раскрыть их природу. Посредством экономического анализа устанавливается причинная связь, взаимосвязь и взаимообусловленность, основные причины и факторы лишь после этого устанавливается характер их влияния на основе построения групповых таблиц. Нельзя строить групповую таблицу для выявления второстепенного фактора.
Объединения однотипных предприятий, представляющие собой качественно однородные совокупности имеют возможность широкого применения типологических, структурных и аналитических группировок.
Типологические группировки формируются по однородным предприятиям в целом и по видам производства (по переделам). Например, в рамках машиностроительного предприятия можно выделить группировки литейного производства (с группировками серого и ковкого чугуна, стального и цветного литья), кузнечного производства, холодной штамповки, термообработки, механической обработки, сварки, сборки, нанесения защитных покрытий, прочих хозяйств (с группировками инструментального, складского, ремонтного и транспортного хозяйства).
Структурные группировки позволяют исследовать внутреннее строение показателей, соотношения их отдельных составляющих и используются при изучении деятельности подразделений и функциональных областей внутри предприятий, как в статике, так и в динамике. При этом группировки формируются по уровням производственной мощности, механизации, по производительности труда, по структуре выпускаемой продукции, работ, услуг (по видам и заданному ассортименту).
Аналитические (причинно-следственные) группировки, по существу, предназначены для выявления наличия, направления и формы связи показателей изучаемых объектов, явлений. По характеру признаков, на основании которых строится аналитическая группировка, она может быть качественной (когда выбранный признак построения не имеет количественного выражения) или количественной. По сложности построения различают два типа группировок – простые и комбинированные. С помощью простых группировок изучается взаимосвязь между явлениями, сгруппированными по какому-либо одному признаку. В комбинированных группировках деление изучаемой совокупности сначала производится по одному признаку, а затем внутри каждой группировки – по другому признаку и т.д. Таким образом, могут быть построены двух-, трех-, четырехуровневые группировки и т.д. По форме они соответствуют типологическим и структурным группировкам. При построении аналитических группировок из двух взаимосвязанных показателей один из них рассматривается в качестве фактора, влияющего на второй показатель, рассматривается как результат влияния первого показателя (и наоборот, факторный признак может выступать в качестве результативного).
Информационной основой группировки служит выборочная совокупность однотипных объектов. Выборочная совокупность конструируется по формуле случайной безвозвратной выборки:
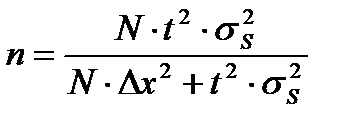 , (2.28)
, (2.28)
где 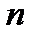 - необходимый объем выборки;
- необходимый объем выборки;
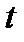 - коэффициент доверия;
- коэффициент доверия;
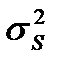 - общая выборочная дисперсия;
- общая выборочная дисперсия;
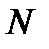 - объем генеральной совокупности;
- объем генеральной совокупности;
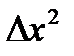 - предельная ошибка выборочной средней.
- предельная ошибка выборочной средней.
В табл. 2.3 представлен пример четырехфакторной группировки промышленных предприятий региона по уровню задолженности по платежам в бюджеты по налогу на прибыль. Определяющим фактором является рентабельность производства. От этого показателя зависит показатель уровня расходов на оплату труда и платежей по единому социальному налогу, а также показатель годового объема реализации продукции.
Таблица 2.3 – Группировка промышленных предприятий региона по уровню задолженности
по налогу на прибыль
| Группы предприятий по размерам задолженности по налогу на прибыль, млн. руб. | Рентабельность производства, % | Затраты на оплату труда на одного работающего, тыс. руб./год | Годовой объем реализации продукции, млрд. руб. |
| До 50 | 5,8 | 58,2 | 58,2 |
| 51 – 100 | 4,5 | 57,7 | 93,6 |
| 101 – 300 | 3,3 | 54,5 | 95,1 |
| 501 – 750 | 3,2 | 58,3 | 162,8 |
| 751 – 1000 | 2,7 | 57,1 | 110,5 |
| 1001 – 1300 | 2,1 | 53,9 | 92,8 |
| 1301 – 1600 | 1,8 | 52,0 | 88,0 |
| 1601 – 2000 | 1,5 | 55,5 | 71,7 |
| 2001 – 2500 | 1,3 | 57,4 | 23,8 |
| 2501 – 3000 | 1,1 | 56,3 | 31,6 |
| Свыше 3000 | 0,8 | 50,6 | 22,9 |
| В ЦЕЛОМ | 2,2 | 57,0 | 851,0 |
Аналитичность табл. 2.3 достаточно высока: чем ниже рентабельность производства на предприятиях, тем выше уровень задолженности по платежам по налогу на прибыль. Как правило, рост рентабельности производства благоприятно сказывается как на годовом объеме реализации продукции предприятия (рост доли рынка сбыта), так и на уровне заработной платы в расчете на одного работающего на предприятии.
В табл. 2.4 представлен пример четырехфакторной группировки по некоторой совокупности торговых предприятий, определяющим фактором в которой является объем товарооборота.
От показателя объема товарооборота зависят показатели среднегодового оборота на одного работника (производительность труда), товарных запасов (скорость товарооборота) и уровня издержек обращения. Очевидна высокая аналитичность приведенной таблицы 3.2: рост объема товарооборота весьма благоприятно сказывается на всех перечисленных выше показателях деятельности.
Правильная группировка показателей дает возможность исследовать зависимость между ними, более глубоко разобраться в сущности экономических явлений, систематизировать материалы анализа, определить главное, характерное, типичное. Одним из важнейших вопросов при проведении исследований является вопрос выбора интервала группировки. С этой целью применяются два подхода.
Первый подход предполагает деление всей совокупности данных на группы с равными интервалами значений. Этот подход используется наиболее часто, так как при выборе границ интервалов отсутствует элемент субъективизма. В рамках этого подхода длина интервала группировки определяется по следующим формулам Стерджеса:
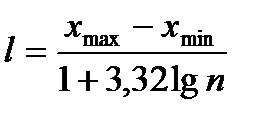 ; (2.29)
; (2.29)
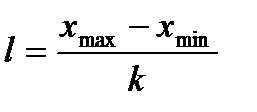 , (2.30)
, (2.30)
где 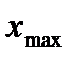 - максимальное значение признака в исследуемой совокупности данных;
- максимальное значение признака в исследуемой совокупности данных;
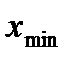 - минимальное значение признака в исследуемой совокупности данных;
- минимальное значение признака в исследуемой совокупности данных;
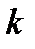 - число групп с одинаковой длиной интервала;
- число групп с одинаковой длиной интервала;
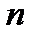 - число наблюдений.
- число наблюдений.
Таблица 2.4 – Группировка специализированных магазинов по объему товарооборота
| Группы магазинов по размерам розничного товарооборота, млн. руб. | Среднегодовой оборот на одного работника, тыс. руб. | Товарные запасы, суток | Уровень издержек обращения, % к обороту |
| До 150 | 444 | 59 | 9,94 |
| 151 – 200 | 481 | 53 | 9,15 |
| 201 – 300 | 547 | 51 | 8,79 |
| 301 – 400 | 622 | 44 | 8,45 |
| 401 – 600 | 844 | 41 | 8,32 |
| 601 – 800 | 921 | 38 | 8,12 |
| 801 – 1000 | 1210 | 34 | 7,95 |
| 1001 – 1200 | 1346 | 30 | 7,73 |
| 1201 – 1500 | 1781 | 27 | 7,57 |
| 1501 – 2000 | 2055 | 23 | 7,13 |
| Свыше 2000 | 2320 | 21 | 6,52 |
| В ЦЕЛОМ | 648 | 49 | 8,88 |
Очевидно, что знаменатель дроби в формуле (2.29) численно равен количеству групп или интервалов, на которое разбивается исследуемая совокупность данных. Таким образом, можно рассчитать оптимальное число групп, соответствующее некоторому числу наблюдений, согласно формуле Стерджеса (табл. 2.5).
Таблица 2.5 – Результаты расчета оптимального числа групп согласно формуле Стерджеса
Число наблюдений 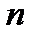
| 9-14 | 15-24 | 25-44 | 45-89 | 90-164 |
Число групп 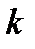
| 4 | 5 | 6 | 7 | 8 |
Прямое применение формулы Стерджеса предполагает отсутствие каких-либо ограничений на параметры группировки. Однако, возможно введение таких ограничений. Например, заранее устанавливается количество групп 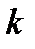 исходя из представлений аналитика о качественной однородности выделяемых групп единиц совокупности. В таком случае длина интервала группировки определяется по формуле (2.30).
исходя из представлений аналитика о качественной однородности выделяемых групп единиц совокупности. В таком случае длина интервала группировки определяется по формуле (2.30).
В соответствии со вторым подходом интервалы группировки можно выбирать равными или неравными, как возрастающими, так и убывающими. Такой подход обычно применяется в тех случаях, когда имеет место большая вариация ( 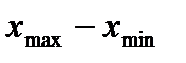 ) и неравномерность распределения признака по всему интервалу его изменения. При выборе размера интервала группировки руководствуются здравым смыслом и логикой, опираясь при этом на опыт и традиционно сложившиеся подходы в группировке данных. При втором подходе интервалы часто выбирают таким образом, чтобы группы оказались равнозаполненными.
) и неравномерность распределения признака по всему интервалу его изменения. При выборе размера интервала группировки руководствуются здравым смыслом и логикой, опираясь при этом на опыт и традиционно сложившиеся подходы в группировке данных. При втором подходе интервалы часто выбирают таким образом, чтобы группы оказались равнозаполненными.
Индексный метод. Всякий индекс исчисляется соизмерением отчетной величины с базисной величиной. При этом сравниваются в относительных числах производительность труда, цены, товарооборот, объемы производства, затраты на производство и реализацию продукции (работ, услуг) и т.д. Под индексом понимается статистический относительный показатель, характеризующий соотношение во времени (динамические индексы) или в пространстве (территориальные индексы) разнообразных социально-экономических явлений – цен отдельных товаров, объемов производства и реализации продукции (работ, услуг), себестоимости и других [4].
Выделяют индивидуальные и сводные индексы. Индивидуальные (частные) индексы выражают соотношение непосредственно соизмеримых величин и являются исходными для индексных расчетов. К таким индексам относятся, например, индексы реализации определенного вида продукции (работ, услуг) в отчетном и базисном периодах. Сводные индексы включают разновидности групповых и общих индексов и характеризуют соотношения сложных явлений. К таким индексам относятся, например, групповой индекс продукции легкой промышленности или общий индекс объема розничного товарооборота по району. По существу, групповые (общие) индексы представляют собой некоторую среднюю величину из индивидуальных (частных) индексов. Таким образом, групповой (общий) индекс всегда меньше, чем наибольший из индивидуальных (частных) индексов, и всегда больше, чем минимальный из них.
Расчет индивидуального (частного) индекса ведется путем деления величины исследуемого элемента (показателя) в отчетном периоде на соответствующую величину этого элемента (показателя) в базисном периоде. Например, формула для расчета индивидуального индекса ( 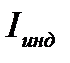 ), характеризующего изменение цены определенного товара в отчетном периоде по сравнению с базисным, будет выглядеть так:
), характеризующего изменение цены определенного товара в отчетном периоде по сравнению с базисным, будет выглядеть так:
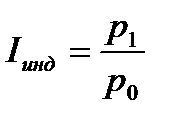 , (2.31)
, (2.31)
где 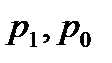 - цена данного товара соответственно в отчетном и базисном периодах.
- цена данного товара соответственно в отчетном и базисном периодах.
Общая формула для расчета индивидуальных индексов такова:
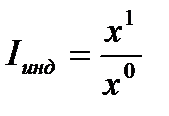 , (2.32)
, (2.32)
где 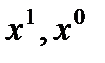 - индексируемый показатель, соответственно, в отчетном и базисном периодах.
- индексируемый показатель, соответственно, в отчетном и базисном периодах.
Расчет группового индекса может производиться по формулам агрегатного индекса, среднего арифметического индекса, среднего гармонического индекса.
Агрегатный индекс является основной формой сводных индексов и характеризует относительные изменения индексируемого показателя в отчетном периоде по сравнению с базисным периодом. Числитель и знаменатель агрегатных индексов представляют собой суммы произведений индексируемого показателя и его веса за два сравниваемых периода.
Формула агрегатного индекса с весами текущего периода:
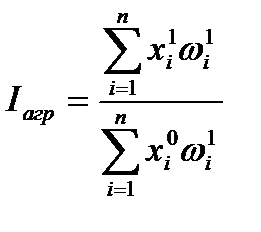 , (2.33)
, (2.33)
где 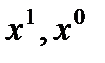 - индексируемые показатели, соответственно, в отчетном и базисном периодах;
- индексируемые показатели, соответственно, в отчетном и базисном периодах;
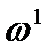 - веса индексов в отчетном периоде;
- веса индексов в отчетном периоде;
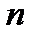 - количество разновидностей индексируемого показателя.
- количество разновидностей индексируемого показателя.
Формула агрегатного индекса с весами базисного периода:
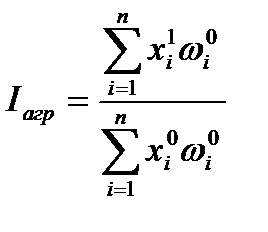 , (2.34)
, (2.34)
где 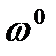 - веса индексов в базисном периоде.
- веса индексов в базисном периоде.
Агрегатный индекс с совместным изменением обоих показателей:
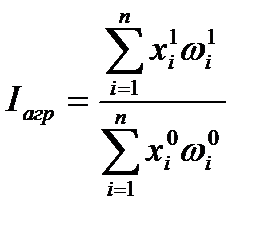 . (2.35)
. (2.35)
В системе анализа коммерческой деятельности важную роль играет исследование динамики индекса ассортиментных сдвигов в товарообороте. Указанный индекс показывает изменение товарооборота за счет сдвигов в внутригрупповой, ассортиментной структуре продажи товаров. Данный индекс ( 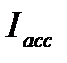 ) строится по следующей формуле:
) строится по следующей формуле:
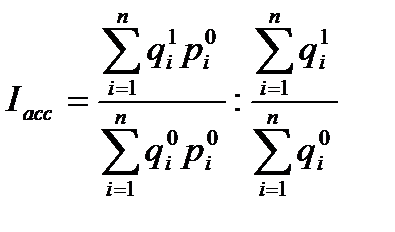 , (2.36)
, (2.36)
где 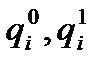 - количество i–го сорта товара, реализованного, соответственно, в базисном и отчетном периодах;
- количество i–го сорта товара, реализованного, соответственно, в базисном и отчетном периодах;
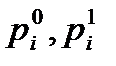 - цена i–го вида (сорта) товара соответственно в базисном и отчетном периодах;
- цена i–го вида (сорта) товара соответственно в базисном и отчетном периодах;
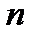 - количество видов (сортов) реализуемого товара в ассортименте.
- количество видов (сортов) реализуемого товара в ассортименте.
В практике экономического анализа коммерческой деятельности достаточно часто используется целый ряд других индексов.
Например, индекс издержкоемкости товарооборота, характеризующий влияние на динамику среднего уровня издержек обращения изменений состава товарооборота по ряду признаков:
- по товарам;
- по видам оборотов (складской и транзитный в оптовой торговле);
- по торговым системам и другим.
Исчисляется индекс издержкоемкости товарооборота как отношение двух сумм издержек, рассчитанных на одинаковые по объему, но разные по структуре суммы товарооборота при равных групповых уровнях издержек обращения (обычно это издержки базисного периода):
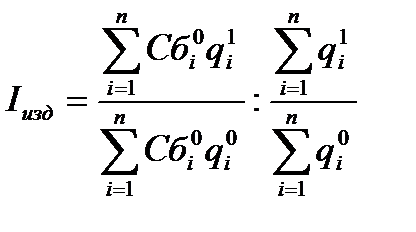 , (2.37)
, (2.37)
где 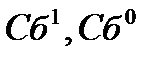 - уровни издержек обращения по группам товаров (равны частному от деления общей суммы издержек на сумму товарооборота по группам товаров), соответственно, в отчетном и базисном периодах;
- уровни издержек обращения по группам товаров (равны частному от деления общей суммы издержек на сумму товарооборота по группам товаров), соответственно, в отчетном и базисном периодах;
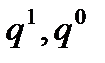 - товарооборот по группам товаров, соответственно, в отчетном и базисном периодах;
- товарооборот по группам товаров, соответственно, в отчетном и базисном периодах;
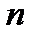 - количество рассматриваемых групп товаров в общем объеме товарооборота.
- количество рассматриваемых групп товаров в общем объеме товарооборота.
Индекс физического объема розничного товарооборота отражает динамику товарооборота в сопоставимых ценах и исчисляются отдельно по каждой товарной группе, по продовольственным и непродовольственным товарам. Когда количество товаров измеряется в натуральных единицах, используется агрегатная форма этого индекса ( 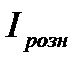 ):
):
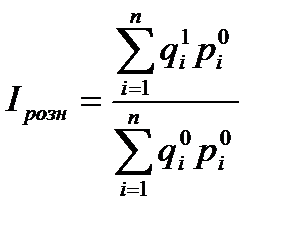 , (2.38)
, (2.38)
где 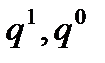 - объемы реализации товаров по товарным группам, соответственно, в отчетном и базисном периодах;
- объемы реализации товаров по товарным группам, соответственно, в отчетном и базисном периодах;
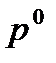 - цены товаров по группам базисного периода;
- цены товаров по группам базисного периода;
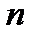 - количество рассматриваемых товарных групп.
- количество рассматриваемых товарных групп.
В тех же случаях, когда продажа товаров учитывается в денежных единицах, индекс физического объема розничного товарооборота строится по формуле, в которой в числителе товарооборот отчетного периода 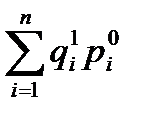 пересчитывается в базисные цены:
пересчитывается в базисные цены:
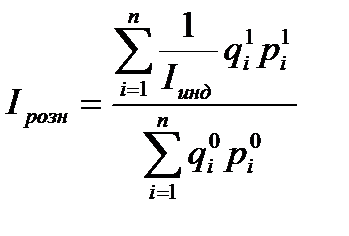 . (2.39)
. (2.39)
Индекс поставки товаров ( 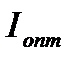 ) характеризует динамику оптового товарооборота. При этом используется система индексов товарооборота в сопоставимых ценах. Так как поставка продовольственных товаров учитывается в натуральных единицах, то их индекс поставки строится по агрегатной форме. Так как поставка непродовольственных товаров учитывается в денежных единицах, то их индекс поставки строится по формуле индекса физического объема товарооборота с использованием индивидуальных индексов цен. В общем индексе поставки товаров (включая продовольственные и непродовольственные товары) числитель агрегируется из числителей двух предыдущих индексов, а знаменатель – из их знаменателей:
) характеризует динамику оптового товарооборота. При этом используется система индексов товарооборота в сопоставимых ценах. Так как поставка продовольственных товаров учитывается в натуральных единицах, то их индекс поставки строится по агрегатной форме. Так как поставка непродовольственных товаров учитывается в денежных единицах, то их индекс поставки строится по формуле индекса физического объема товарооборота с использованием индивидуальных индексов цен. В общем индексе поставки товаров (включая продовольственные и непродовольственные товары) числитель агрегируется из числителей двух предыдущих индексов, а знаменатель – из их знаменателей:
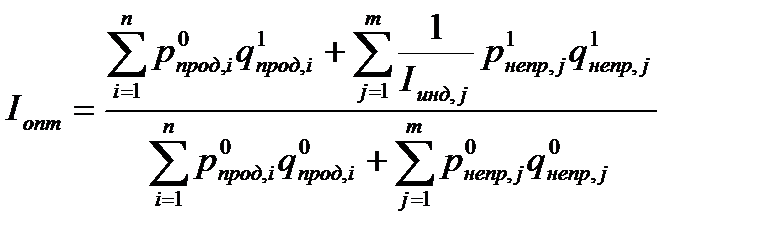 , (2.40)
, (2.40)
где 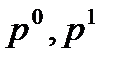 - розничные цены продовольственных и непродовольственных товаров в базисном и отчетном периодах;
- розничные цены продовольственных и непродовольственных товаров в базисном и отчетном периодах;
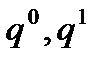 - количество поставленных продовольственных и непродовольственных товаров в базисном и отчетном периодах;
- количество поставленных продовольственных и непродовольственных товаров в базисном и отчетном периодах;
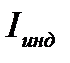 - индивидуальные (или групповые) индексы розничных цен;
- индивидуальные (или групповые) индексы розничных цен;
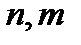 - количество ассортиментных групп соответственно продовольственных и непродовольственных товаров.
- количество ассортиментных групп соответственно продовольственных и непродовольственных товаров.
В экономическом анализе широко используются такие индексы:
- индекс средних розничных цен;
- индекс структурных сдвигов;
- индекс стоимости основных фондов;
- индекс тарифный (транспортный);
- индекс территориальный;
- индекс трудоемкости товарооборота;
- индекс физического объема внешней торговли;
- индекс физического объема продукции;
- индекс цен внешней торговли;
- индекс цен потребительских товаров и услуг;
- индексы закупочных цен;
- индексы оптовых цен на промышленную продукцию;
- индексы производительности труда в торговле;
- индексы себестоимости строительной продукции;
- индексы соотношения цен;
- индексы цен и тарифов на услуги;
- индексы цен на продукцию строительства;
- индексы цепные;
- индексы биржевые (фондовые);
- индексы валютной корзины;
- индекс деловой активности;
- индекс заработной платы;
- индекс конкурентоспособности промышленных товаров;
- индекс котировки (курсов) акций;
- индекс курсов;
- индекс сбыта;
- индекс себестоимости;
- индекс цен и тарифов на услуги населению;
- индекс цен по капиталовложениям и др.
Математико-статистические методы изучения связей в современных системах экономического анализа применяются весьма широко и включают корреляционный, регрессионный, дисперсионный, кластерный анализ. Указанные методы используются в системе стохастического моделирования и, в определенной степени, представляют собой дополнение и углубление системы детерминированного анализа [4, 5]. При использовании этих методов требуется обеспечить достижение следующих целей:
- оценка уровней влияния факторов на результативный показатель, по которым нельзя построить жестко детерминированную модель;
- изучение и сравнение уровней влияния факторов, которые невозможно включить в одну и ту же детерминированную модель;
- выделение и оценка уровней влияния сложных факторов, которые не могут быть выражены каким-то одним количественным показателем.
Применение стохастического подхода, в отличие от детерминированного подхода, требует выполнения некоторых предпосылок. Прежде всего, это требование наличия достаточно большой совокупности объектов. Так, если для анализа детерминированной модели достаточно даже одного объекта, то для анализа стохастической модели необходима уже совокупность объектов. Кроме того, для стохастического анализа нужен достаточный объем наблюдений, так как лишь по одному-двум наблюдениям нельзя судить о характере стохастической связи. Особенностью использования стохастических моделей в экономике считается трудность получения совокупности данных достаточного объема. Если, например, в ходе технического исследования можно повторить тот или иной эксперимент, то в экономике этого сделать нельзя. Поэтому в системе экономического анализа нередко приходится работать в условиях малых выборок (менее 20 наблюдений). Кроме того, одним из требований статистических расчетов при построении регрессии является достаточность количества наблюдений, которое в 6-8 раз должно превышать количество исследуемых факторов, что в практике экономического анализа наблюдается крайне редко.
Поскольку стохастическая модель, как правило, выражается уравнением регрессии, ее построение требует соблюдения ряда условий:
- случайность наблюдений;
- качественная и количественная однородность совокупности (показателем количественной однородности совокупности является показатель вариации, который рассматривается ниже);
- наличие специального математического аппарата для проведения вычислений.
При этом следует учитывать, что стохастическое моделирование предназначено для решения трех основных задач:
1. Установление факта наличия или отсутствия статистически значимой связи между изучаемыми результативными и факторными признаками.
2. Прогнозирование неизвестных значений результативных показателей по заданным значениям факторных признаков (это, по существу, задачи интерполяции и экстраполяции).
3. Выявление причинных связей между изучаемыми показателями, измерение их тесноты и сравнительный анализ степени влияния.
Проведение стохастического моделирования и выявление связей представляет собой достаточно сложный процесс, состоящий из нескольких этапов, на каждом из которых необходимо выполнить определенные процедуры. Ниже приводятся характеристики основных этапов стохастического моделирования.
Этап 1. Качественный анализ:
- постановка цели анализа;
- определение совокупности данных, используемых для анализа;
- определение результативных признаков;
- определение факторных признаков;
- выбор периода анализа;
- выбор метода анализа.
Этап 2. Предварительный анализ моделируемой совокупности данных:
- проверка однородности совокупности;
- исключение аномальных наблюдений;
- уточнение необходимого объема выборки;
- установление законов распределения изучаемых переменных.
Этап 3. Построение регрессионной модели экономического объекта:
- перебор (чередование, выбор) конкурирующих вариантов построения модели;
- уточнение перечня исследуемых факторов, включаемых в модель;
- расчет оценок параметров уравнений регрессии.
Этап 4. Оценка адекватности модели:
- проверка статистической значимости уравнения регрессии в целом и его отдельных параметров;
- проверка соответствия формальных свойств полученных оценок задачам исследования.
Этап 5. Экономическая интерпретация и практическое использование модели. На данном этапе выполняются следующие действия:
- определение пространственно-временной устойчивости полученных зависимостей;
- оценка прогностических свойств модели.
Перечисленные выше процедуры стохастического анализа имеют ряд методологических особенностей и теоретических аспектов:
1. Для анализа следует брать всю имеющуюся совокупность данных. Если эта совокупность слишком велика, необходимо обеспечить тщательность составления выборки из этой совокупности. Выборки должна быть типичной (практически проверенной) для данного круга явлений, в противном случае анализ не будет иметь смысла, поскольку его результаты не позволят сделать значимые выводы для всей совокупности данных.
2. В качестве результативных признаков в экономическом анализе используют либо показатели экономического эффекта (выручка, товарооборот, объем реализации и т.п.), либо показатели экономической эффективности (рентабельность, оборачиваемость, производительность и т.п.). Более предпочтительно использование не абсолютных, а относительных показателей. Этому есть несколько причин, в том числе сравнимость относительных показателей и большая близость их распределений нормальному закону распределения. Последнее обстоятельство также важно, поскольку нормальность распределения признаков является основной предпосылкой корреляционно-регрессионного анализа.
3. В качестве факторных признаков следует выбирать показатели, которые комплексно характеризуют исследуемое экономическое явление. Также предпочтительнее ориентироваться на относительные показатели.
- В анализе экономических явлений выделяют два подхода – статистический и динамический. Чаще используется статистический подход, так как он отличается относительной простотой и не требует применения сложных математических методов. Динамический анализ (исследование рядов данных во времени) часто предполагает рассмотрение автокорреляционных зависимостей, что требует применения сложного эконометрического инструментария.
5. Предварительная обработка рядов данных начинается с установления законов распределения (распределение должно быть близко к нормальному). В условиях использования малых выборок проверка нормальности распределения проводится путем сравнения эмпирических коэффициентов асимметрии и эксцесса с их средними квадратическими ошибками (их аналитические выражения приводятся ниже). При этом должна быть подтверждена нормальность распределения рядов данных.
6. Проверка однородности сводится к проверке уровня коэффициента вариации. Если совокупность неоднородна, следует исключить из нее наиболее отклоняющиеся, «аномальные» наблюдения, поскольку именно эти наблюдения, скорее всего, нетипичны для данного исследования. Для устранения таких аномальных наблюдений используется правило «трех сигм».
7. Уточнение перечня факторов может осуществляться, например, путем расчета матрицы парных коэффициентов корреляции. Перебор (выбор) конкурирующих вариантов модели, осуществляется, как правило, с использованием компьютеров и прикладных программ.
- Проверка устойчивости модели осуществляется расчетом ее параметров на усеченной или расширенной совокупности, а также на той же совокупности, но уже в другом интервале времени.
При изучении некоторой совокупности данных в системе стохастического моделирования используют ряд специфических характеристик. К таким характеристикам относятся средние значения. При стохастическом анализе больших массивов данных обычно интересуются двумя аспектами:
- величинами, которые характеризуют ряд значений как целого (характеристиками общности);
- величинами, которые описывают различие между членами совокупности (характеристиками вариации, разброса значений).
Так, все средние величины относятся в первой группе показателей (характеристикам общности), поскольку являются характеристиками изучаемой совокупности как целого. Кроме средних величин, в качестве показателей (характеристик) общности также используются такие характеристики как середина интервала, мода, медиана.
Середина интервала возможных значений показателя 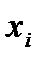 определяется по следующей формуле:
определяется по следующей формуле:
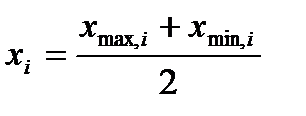 . (2.41)
. (2.41)
Мода представляет собой такое значение изучаемого признака, которое среди всех его значений встречается наиболее часто (можно сказать, что это типичное значение случайной величины). В этом случае говорят об унимодальном распределении. Если же чаще других встречаются два или более различных значений, то такую совокупность данных называют соответственно бимодальной или мультимодальной. Если же ни одно из значений совокупности не встречается чаще других (например, все значения совокупности встречаются по одному разу или равное количество раз), то такая совокупность считается безмодальной.
Медиана представляет собой такое значение изучаемой величины, которое делит изучаемую совокупность на две равные части, в которых количество членов со значениями меньше медианы равно количеству членов со значениями больше медианы. Медиану можно найти только в таких совокупностях, которые содержат нечетное количество членов. В отличие от средней величины, медиана не зависит от крайних значений показателей (если увеличивается максимальное или минимальное значение исследуемого показателя, то вместе с ним возрастают все средние величины, но медиана остается неизменной). Поэтому медиана представляется более удобной характеристикой совокупности в тех случаях, когда совокупность данных неоднородна и имеет резкие флуктуации.








