Матрица определитель которой равен нулю, называется вырожденной.
Геометрический смысл определителя состоит в следующем:
1) модуль определителя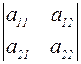 
равен площади параллелограмма, построенного на векторах 
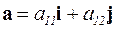и 
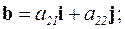
2) модуль определителя
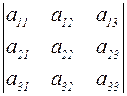
равен объему параллелепипеда, построенного на векторах
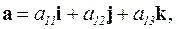
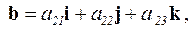
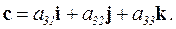
3. Обратная матрица
Матрица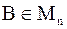 
называется обратной к матрице 
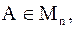если AB =BA = I; при этом пишут 
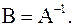Матрица А имеет обратную только в том случае, если она невырожденная, то есть если 
.
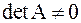Если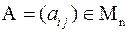 
– невырожденная матрица, то
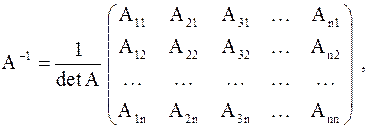
где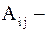 
алгебраические дополнения элементов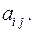 
Пример 4. Найт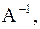и 
если
.
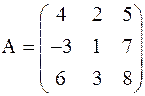Сделать проверку.
Решение.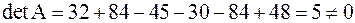 
, следовательно, существует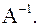 
Найдем алгебраические дополнения:
; 
; 
; 
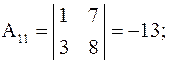
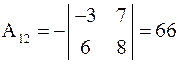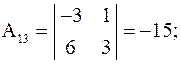
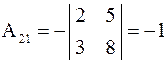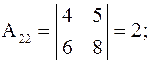
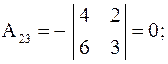
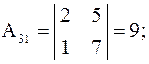
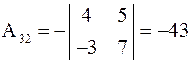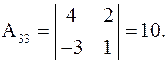
Отсюда получаем
.
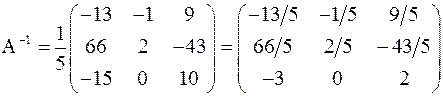Сделаем проверку:
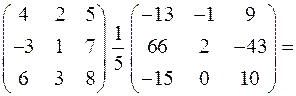
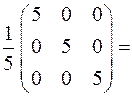
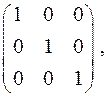
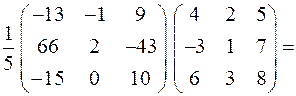
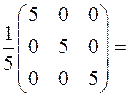
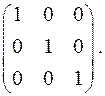
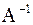найдено верно.
4. Ранг матрицы
Выберем в матрице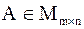 
k строк и k столбцов 
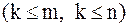. Из элементов, стоящих на пересечении выделенных строк и столбцов, составим определитель k-го порядка, который назовем минором k-го порядка матрицы A.
Пример 5. Найти минор 2-го порядка матрицы
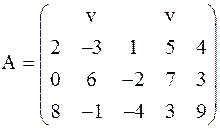
(выбранные строки и столбцы отмечены знаком «v»).
Решение. Имеем
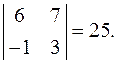
Рангом матрицы A называется неотрицательное целое число r, удовлетворяющее двум условиям:
1) существует по крайней мере один минор порядка r матрицы A, отличный от нуля;
2) все миноры порядка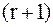 
матрицы A равны нулю.
При этом пишут rank A = r. Если rank A = r, то любой отличный от нуля минор порядка r матрицы A называется базисным минором.
Теорема 2. Максимальное число линейно независимых столбцов матрицы A равно максимальному числу линейно независимых строк матрицы A. Более того, это число равно рангу матрицы A.
Не изменяют ранга матрицы следующие операции:
1) перестановка столбцов или строк;
2) умножение столбца (строки) на число, отличное от нуля;
3) прибавление к столбцу (строке) другого столбца (другой строки), умноженного предварительно на некоторое число;
4) зачеркивание нулевого столбца (строки);
5) транспонирование.
Трапецеидальной матрицей называется матрица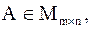 
имеющая вид
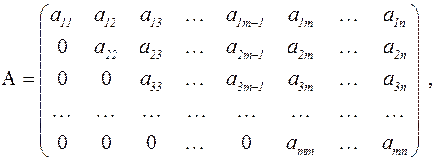
где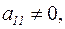 
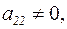
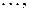
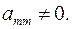Другими словами, матрица 
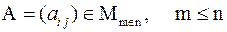является трапецеидальной, если 
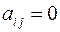при i > j и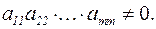 
Ранг трапецеидальной матрицы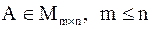 
равен m. Для нахождения ранга матрицы достаточно, пользуясь преобразованиями
1- 4, называемыми элементарными, привести матрицу к трапецеидальному виду.
Пример 6. Найти ранг матрицы
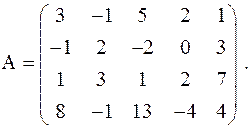
Решение. С помощью элементарных преобразований приведем матрицу A к трапецеидальному виду:
~ 
~
~ 
~ 
~
 |
~ 
~ 
.
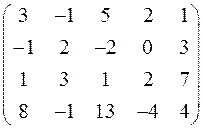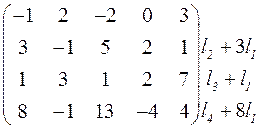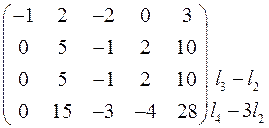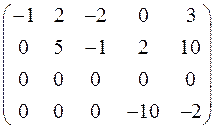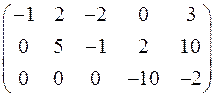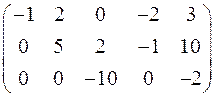Ранг последней матрицы, являющейся трапецеидальной, равен 3; следовательно, rank A = 3.
Из определения ранга следует, что матрица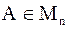 
является невырожденной в том и только в том случае, если rangА = n.
5. Системы линейных алгебраических уравнений