Отчет по Лабораторной работе 4

Дата: 2025-05-25; Просмотры: 2

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Московский государственный технический университет им. Н.Э. Баумана

Факультет «Информатика и системы управления»

Кафедра «Автоматизированные системы обработки информации и управления»

Отчет по Лабораторной работе 4

По курсу

“Оперативный анализ и визуализация данных”

Выполнил:

Алексеев А.В.

Студент группы РТ5-51

Москва 2018

1 Цель лабораторной работы.

Цель работы – получить теоретические знания, изучив алгоритмы, применяемые в машинном обучении, и практические навыки исследования и распознавания образов с применением модели линейной регрессии и логистической регрессии.

2.Теоретические основы предметной области.

Линейная регрессия — метод восстановления зависимости между двумя переменными.

Задача линейной регрессии заключается в нахождении коэффициентов уравнения линейной регрессии, которое имеет вид:

y = b ₀ + b ₁ x ₁ + b ₂ x ₂ + …+ b_nx_n

где y — выходная переменная модели;

x₁, x₂ …x_n — входные (независимые) переменные;

b_i — коэффициенты линейной регрессии, называемые также параметрами модели (b₀ — свободный член). Коэффициенты bi можно выразить через коэффициент корреляции Пирсона, стандартные отклонения и средние значения переменных x и y.

Логистическая регрессия:

Логистическая регрессия (Logistic regression) — метод построения линейного классификатора, позволяющий оценивать апостериорные вероятности принадлежности объектов классам. Логистическая регрессия применяется для предсказания вероятности возникновения некоторого события по значениям множества признаков. Для этого вводится так называемая зависимая переменная y, принимающая лишь одно из двух значений — как правило, это числа 0 (событие не произошло) и 1 (событие произошло), и множество независимых переменных (также называемых признаками, предикторами или регрессорами) — вещественных x1,x2..xn, на основе значений которых требуется вычислить вероятность принятия того или иного значения зависимой переменной. Характерна для задач оценки вероятности некоторого события на основе значений независимых переменных. Также используется для решения задач бинарной классификации, в которых выходная переменная может принимать только два значения — 0 или 1, «Да» или «Нет» и т. д.

3 Задачи лабораторной работы.

· Исследование и оценка распознавания образов с применением модели

линейной регрессии и логистической регрессии с множеством параметров.

· В процессе выполнения лабораторных работ необходимо построить несколько зависимостей (например, зависимость качества обучения от скорости обучения).

4.Результаты, полученные в лабораторной работе.

4.1. Линейная регрессия.

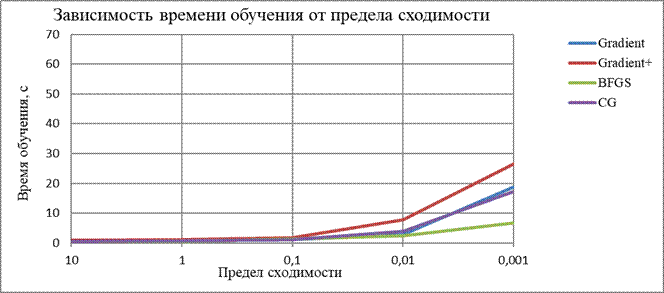
Зависимость времени обучения от предела сходимости
Предел сходимости:	10	1	0,1	0,01	0,001
Градиентный спуск	0,668	0,733	1,216	2,912	18,699
Метод наискорейшего спуска	0,904	1,068	1,674	7,758	26,38
BFGS	0,5	0,575	1,362	2,456	6,614
CG	0,56	0,656	1,093	4,009	17,156

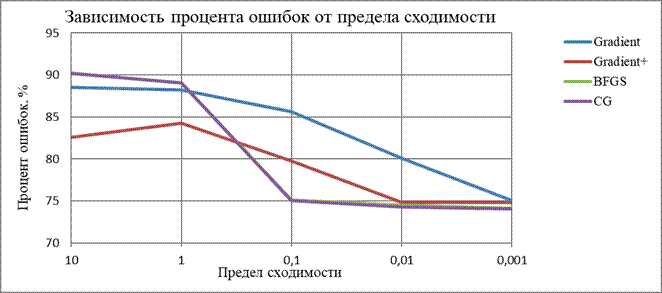
Зависимость процента ошибок от предела сходимости
Предел сходимости:	10	1	0,1	0,01	0,001
Градиентный спуск	88,53	88,23	85,63	80,1	75,07
Метод наискорейшего спуска	82,59	84,24	79,76	74,81	74,78
BFGS	90,2	89,05	75,08	74,5	74,11
CG	90,2	89,05	75,05	74,26	74,04

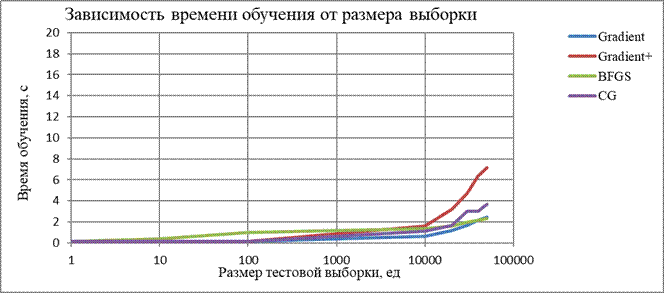
Зависимость времени обучения от размера тестовой выборки
Размер тестовой выборки:	1	10	100	10000	20000	30000	40000	50000
Градиентный спуск	0,116	0,12	0,128	0,655	1,163	1,682	2,148	2,464
Метод наискорейшего спуска	0,126	0,134	0,139	1,601	3,201	4,733	6,351	7,183
BFGS	0,125	0,391	1,008	1,394	1,636	1,966	2,159	2,365
CG	0,117	0,12	0,127	1,134	1,692	3,03	2,996	3,652

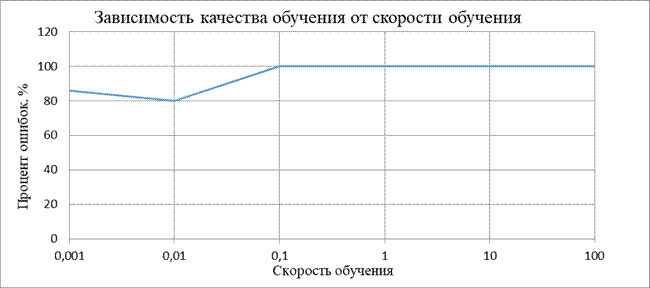
Зависимость качества и времени обучения от скорости обучения для метода градиентного спуска
Скорость обучения:	0,001	0,01	0,1	1	2	5	10	100
Процент ошибок	85,96	80,1	100	100	100	100	100	100
Время обучения	6,25	2,666	8,457	4,135	3,638	3,225	2,87	2,247

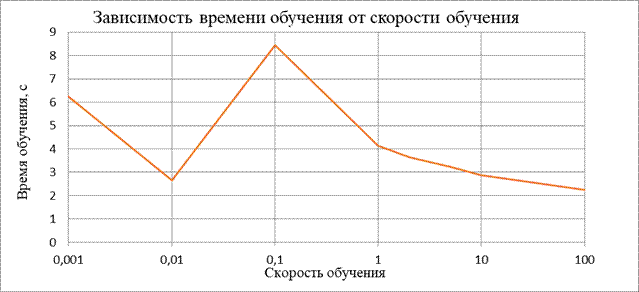
4.2. Логистическая регрессия.

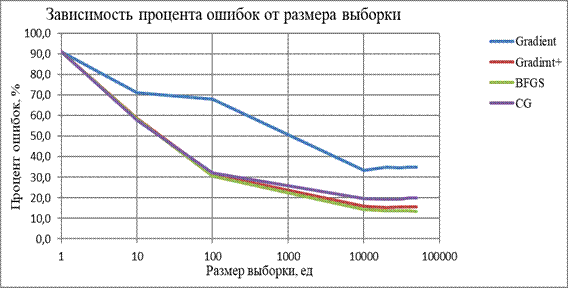
Зависимость процента ошибок от размера выборки
Размер тестовой выборки:	1	10	100	10000	20000	30000	40000	50000
Градиентный спуск	91,08	71,08	68,09	33,30	34,94	34,54	34,93	34,94
Метод наискорейшего спуска	91,08	58,64	31,58	16,01	15,26	15,45	15,46	15,45
BFGS	91,08	58,39	30,68	14,24	13,69	13,59	13,71	13,53
CG	91,08	57,84	32,04	19,55	19,44	19,38	20,11	19,91

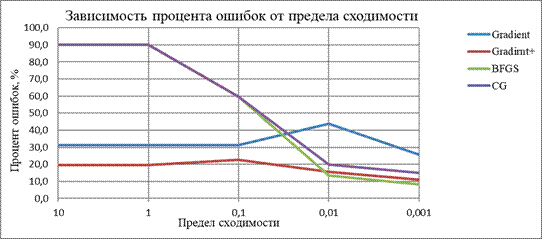
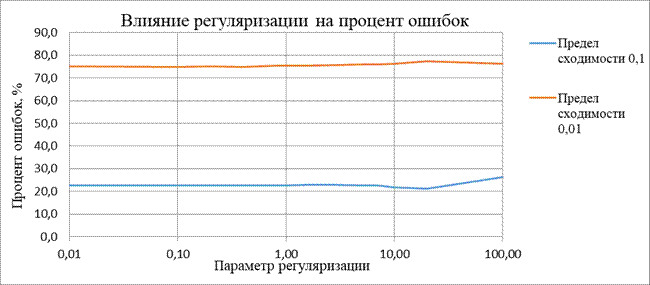
Зависимость процента ошибок от предела сходимости
Предел сходимости:	10	1	0,1	0,01	0,001
Градиентный спуск	31,20	31,20	31,20	43,94	25,81
Метод наискорейшего спуска	19,52	19,52	22,65	15,45	10,94
BFGS	90,20	90,20	59,77	13,53	8,34
CG	90,20	90,20	59,77	19,91	15,11

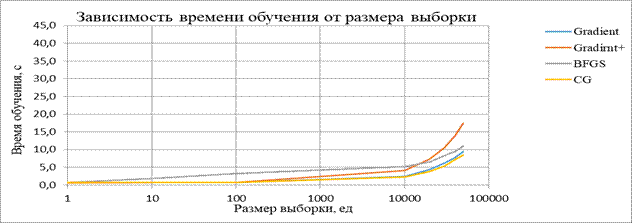
Зависимость времени обучения от размера тестовой выборки
Размер тестовой выборки:	1	10	100	10000	20000	30000	40000	50000
Градиентный спуск	0,607	0,624	0,657	2,355	4,336	6,198	7,766	9,453
Метод наискорейшего спуска	0,619	0,642	0,695	4,001	7,321	10,580	13,895	17,352
BFGS	0,701	1,744	3,166	5,182	6,413	8,280	9,468	10,932
CG	0,655	0,657	0,683	2,185	3,766	5,298	7,089	8,431

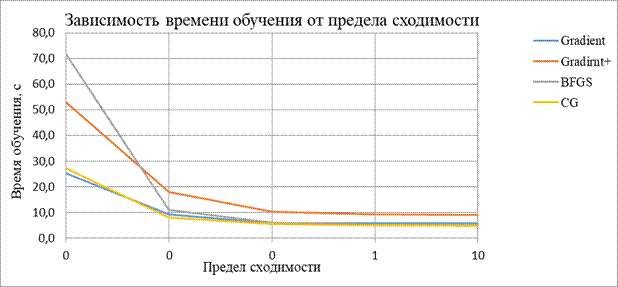
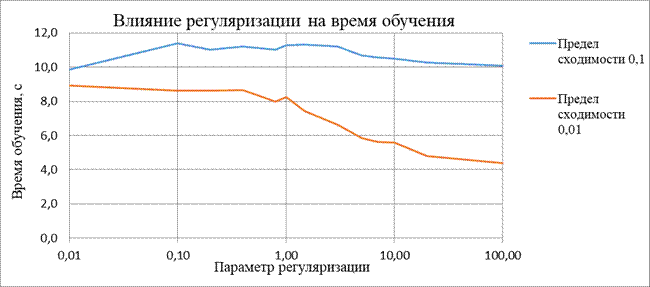
Зависимость времени обучения от величины предела сходимости
Предел сходимости:	10	1	0,1	0,01	0,001
Градиентный спуск	5,828	5,768	5,810	9,104	25,149
Метод наискорейшего спуска	8,910	9,203	10,116	18,083	52,975
BFGS	5,201	5,173	6,012	11,067	71,697
CG	4,710	5,002	5,533	8,072	27,218

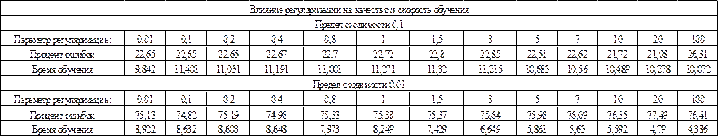
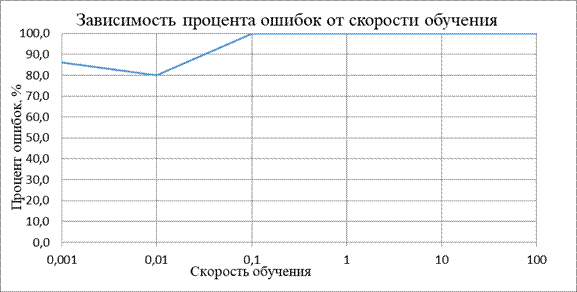
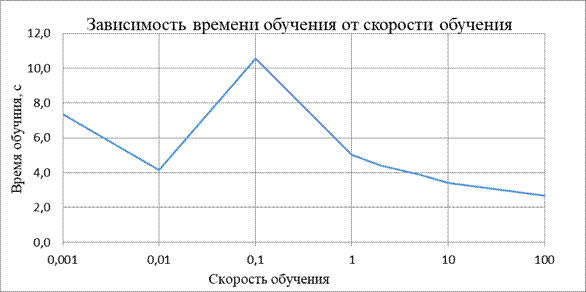
Для градиентного спуска влияние скорости обучения на качество и время обучения
Скорость обучения:	0,001	0,01	0,1	1	2	5	10	100
Процент ошибок	85,96	80,1	100	100	100	100	100	100
Время обучения	7,342	4,143	10,565	5,047	4,425	3,882	3,42	2,665

6.5 Выводы.

Изучил принципы алгоритмов машинного обучения, в частности, линейную и логистическую регрессию. Подкрепил теоретические навыки практическими исследованиями зависимостей основных параметров.