Московского инженерно- физического института
Министерство образования и науки Российской Федерации
ОЗЕРСКИЙ ТЕХНОЛОГИЧЕСКИЙ ИНСТИТУТ
(филиал)
Московского инженерно- физического института
( государственного университета) 
Лабораторная работа №15
Исследование спектра дифракционной решетки
По курсу
Физика (Оптика)
| Преподаватель | Карпов В. И. | ||||
| Выполнил студент группы | 1ТМ-20ДС 1МХ-39 | Куликов Н. В. Клюшин В. А. | |||
| индекс группы | (дата, подпись) | (Ф.И.О.) |
г. Озёрск
2011
| Цель работы: | измерение длин волн видимой части спектра |
| Приборы и принадлежности: | а) источник света в кожухе, б) раздвижная щель, в) собирающая линза, г) дифракционная решетка, д) матовая стеклянная шкала с ползунками и держателями |
ВВЕДЕНИЕ
Дифракционная решетка представляет собой систему параллельных одинаковых щелей, расположенных на равных расстояниях друг от друга. Решетки могут работать на пропускание света – в этом случае дифракционная картина наблюдается в проходящих лучах, широко распространены также металлические отражательные решетки, дающие дифракционную картину в отраженных лучах.
Простейшая дифракционная решетка, работающая на пропускание света, представляет собой стеклянную пластинку, на которой алмазным резцом с помощью делительной машины наносится рад параллельных штрихов. Эти штрихи образуют непрозрачные промежутки между неповрежденными участками пластины, которые и выполняют роль щелей.
Расстояние между серединами соседних щелей называется периодом или постоянной решетки. Период решетки d равен сумме ширины непрозрачного промежутка a и ширины щели b: d=а+b. Эта величина является одной из основных характеристик дифракционной решетки.
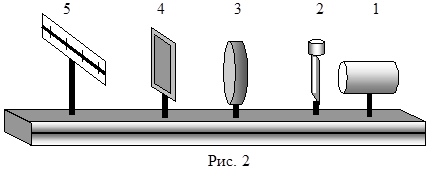
Пусть на дифракционную решетку падает плоская монохроматическая волна и фронт волны параллелен плоскости решетки (рис. 1). Тогда по принципу Гюйгенса каждая точка щели становится самостоятельным источником вторичных волн, распространяющихся по всем направлениям. При этом световые лучи отклоняются от первоначального направления на различные углы дифракции a, огибают препятствия - непрозрачные промежутки – и заходят в область геометрической тени.
Дифракционная картина, возникающая от решетки наблюдается или в бесконечности, или в фокальной плоскости линзы Л на экране Э. Лучи дифрагирующие под одинаковыми углами a, собираются линзой в некоторой точке Р экрана.
|
Рис. 1 |
Принцип Гюйгенса-Френеля позволяет рассчитать интенсивность света в различных точках экрана. Согласно этому принципу, интенсивность в данной точке экрана 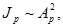 где Ар – результирующая амплитуда колебаний, пришедших в точку Р от всех щелей решетки. Результирующая амплитуда колебаний Ар является векторной суммой амплитуд колебаний создаваемых в точке Р каждой щелью:
где Ар – результирующая амплитуда колебаний, пришедших в точку Р от всех щелей решетки. Результирующая амплитуда колебаний Ар является векторной суммой амплитуд колебаний создаваемых в точке Р каждой щелью:
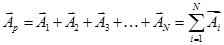 (1)
(1)
 |
Модули всех этих векторов одинаковы и зависят от угла a.
Для тех углов a, для которых разность хода лучей 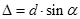 удовлетворяет условию:
удовлетворяет условию:
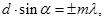 (2)
(2)
где m=0, 1, 2, 3, … и т.д., колебания, приходящие в точку Р от отдельных щелей, усиливают друг друга и амплитуда в точке Р будет максимальна. Формула (2) определяет положение главных максимумов интенсивности, целые числа m называются порядком главного максимума.
Главные максимумы располагаются симметрично по обе стороны относительно центрального главного максимума нулевого порядка (m=0).
При освещении решетки монохроматическим светом с длиной волны l, главные максимумы имеют вид светлых полос, цвет которых определяется длиной волны падающего света.
Если же решетка освещается не монохроматическим светом, т.е. светом с различными длинами волн, то, вследствие зависимости угла дифракции от длины волны, ( 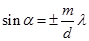 ), главные максимумы соответствующие различным длинам волн l окажутся в различных местах экрана. Дифракционная картина тогда представит, как говорят, спектр падающего на решетку света.
), главные максимумы соответствующие различным длинам волн l окажутся в различных местах экрана. Дифракционная картина тогда представит, как говорят, спектр падающего на решетку света.
Таким образом, дифракционная решетка является спектральным прибором и как всякий спектральный прибор характеризуется дисперсией D и разрешающей способностью R.
Дисперсия определяет протяженность (ширину) дифракционного спектра. Дисперсией называется величина
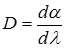 (3),
(3),
где da - угловое расстояние между двумя спектральными линиями, длины волн которых различаются на dl. Из формулы (2) при малых углах sina~a, и для дисперсии получается выражение, не зависящее от l:
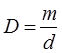 (4)
(4)
Отсюда следует, что при малых углах дисперсии растянутость дифракционного спектра зависит от постоянной решетки d и порядка спектра m и одинакова во всех областях длин волн. 
Разрешающей способностью дифракционной решетки называют безразмерную величину
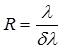 (5),
(5),
где dl - минимальная разность длин волн двух спектральных линий, при которой эти линии воспринимаются раздельно (разрешаются), l - длина волны, около которой происходит разрешение.
Для дифракционной решетки разрешающая способность пропорционально порядку спектра m и числу щелей решетки N:
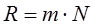 (6).
(6).
Более подробно теория дифракционной решетки изложена в учебниках, список которых приведен в конце сборника.
СХЕМА ОПЫТА
|
|
Установка, на которой наблюдается дифракция от дифракционной решетки, приведена на Рис. 2.
На оптической скамье в специальных держателях последовательно располагаются: источник света – лампа накаливания в кожухе – 1, раздвижная щель – 2, конденсор-3, дифракционная решетка – 4, матовая шкала с миллиметровыми делениями – 5, являющаяся экраном, на котором наблюдается дифракционная картина.
Дифракционная к  артина наблюдается не в фокальной плоскости, а на удаленном, на возможно большее расстояние от решетки экране – 5. В этом случае приближенно выполняется условие наблюдение дифракционной картины в «бесконечности». Лучи дифрагирующие под углом a, падая на экран, образуют систему максимумов различных порядков m=0, ±1, ±2, ±3, … (см рис. 1).
артина наблюдается не в фокальной плоскости, а на удаленном, на возможно большее расстояние от решетки экране – 5. В этом случае приближенно выполняется условие наблюдение дифракционной картины в «бесконечности». Лучи дифрагирующие под углом a, падая на экран, образуют систему максимумов различных порядков m=0, ±1, ±2, ±3, … (см рис. 1).
По расстоянию 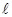 от решетки до экрана и расстоянию S от нулевого максимума до максимума прядка m легко определить углы дифракции для максимума любого порядка:
от решетки до экрана и расстоянию S от нулевого максимума до максимума прядка m легко определить углы дифракции для максимума любого порядка:
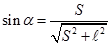 (7).
(7).
ИЗМЕРЕНИЯ
1. Осветив равномерно щель и отрегулировав её ширину и высоту, перемещением линзы 3 получите на шкале четкую картину дифракционных спектров нескольких порядков. Понаблюдайте положение спектров (наблюдение ведется на просвет) и объясните:
· их образование,
· симметричное расположение спектров относительно нулевого максимума,
· ослабление интенсивности по мере увеличения порядка спектра,
· образование в центральном максимуме белой полосы.
2. Определите приближенно длины волн, ограничивающие видимую область сплошного спектра лампы накаливания. Для этого измерьте расстояние 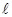 от экрана до дифракционной решетки и расстояние S от нулевого максимума до фиолетовой и красной границ наблюдаемых порядков спектров. Измерения проделайте при двух значениях расстояния
от экрана до дифракционной решетки и расстояние S от нулевого максимума до фиолетовой и красной границ наблюдаемых порядков спектров. Измерения проделайте при двух значениях расстояния 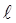 . Рассчитайте соответствующие углы дифракции по формуле (7). Все измерения и вычисления занесите в Таблицу.
. Рассчитайте соответствующие углы дифракции по формуле (7). Все измерения и вычисления занесите в Таблицу.
3. По вычисленным углам и известной постоянной решетки d, используя формулу (2) рассчитайте длины волн фиолетовой и красной границ спектров всех наблюдаемых порядков.
4. Найдите средние значения длин волн, ограничивающих видимую область спектра лампы накаливания.
5. Определите ошибку опыта.
ХОД РАБОТЫ
d=0,01 мм
| L | Фиолетовая граница | Красная граница | ||||||
| m | S | sinj | l, *10-3 | m | S | sinj | l, *10-3 | |
| 125мм | 1 | 6 | 0,43 | 4,3 | 1 | 9 | 0,58 | 5,8 |
| -6 | -0,43 | -9 | -0,58 | |||||
| 2 | 12 | 0,69 | 3,45 | 2 | 15 | 0,76 | 3,8 | |
| -12 | -0,69 | -15 | -0,76 | |||||
| 3 | 18 | 0,82 | 2,73 | 3 | 24 | 0,89 | 2,96 | |
| -18 | -0,82 | -24 | -0,89 | |||||
| 180мм | 1 | 9 | 0,44 | 4,4 | 1 | 12 | 0,55 | 5,5 |
| -9 | -0,44 | -12 | -0,55 | |||||
| 2 | 18 | 0,71 | 3,55 | 2 | 24 | 0,8 | 4 | |
| -18 | -0,71 | -24 | -0,8 | |||||
| 3 | 28 | 0,84 | 2,8 | 3 | 36 | 0,89 | 2,96 | |
| -28 | -0,84 | -36 | -0,89 | |||||
ВЫВОД
Измерили длины волн видимой части спектра.
 |