2. Найти полустепени исхода и захода вершины.
Задача 1
Ориентированный граф
1. Построить матрицы, смежности, инцидентности.
2. Найти полустепени исхода и захода вершины.
Матрица смежности
Матрица смежности графа G с конечным числом вершин n (пронумерованных числами от 1 до n) — это квадратная матрица A размера n, в которой значение элемента aij равно числу рёбер из i-й вершины графа в j-ю вершину.
| V1 | V2 | V3 | V4 | V5 | V6 | |
| V1 | 0 | 1 | 1 | 0 | 1 | 0 |
| V2 | 0 | 1 | 0 | 0 | 1 | 0 |
| V3 | 0 | 0 | 0 | 0 | 0 | 0 |
| V4 | 0 | 0 | 1 | 0 | 0 | 0 |
| V5 | 0 | 0 | 0 | 1 | 0 | 0 |
| V6 | 1 | 1 | 0 | 0 | 1 | 1 |
Матрица инцидентности
| U1 | U2 | U3 | U4 | U5 | U6 | U7 | U8 | U9 | U10 | |
| V1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | -1 | 0 |
| V2 | -1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| V3 | 0 | -1 | 0 | 0 | -1 | 0 | 0 | 0 | 0 | 0 |
| V4 | 0 | 0 | 0 | 0 | 1 | -1 | 0 | 0 | 0 | 0 |
| V5 | 0 | 0 | 0 | -1 | 0 | -1 | -1 | -1 | 0 | 0 |
| V6 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 |
Найдём степени полуисхода и полузахода
Полустепенью исхода (захода) вершины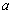 
графа 
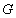будем называть число 
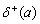(соответственно 
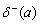), равное количеству дуг графа, исходящих из вершины 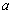(заходящих в вершину 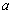). Вклад каждой петли, инцидентной вершине 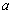, равен 1 как в 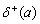, так и в .
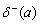Задача 2
Определим полустепени исхода и захода вершины данного графа:
Для вершины V1:
d1+=1, d1- =1
Для вершины V2:
d2+=1, d2-=1
Для вершины V3:
d3+=2, d3-=0
Для вершины V4:
d4+=1 d4-=1
Для вершины V5:
d5+=3 d5-=1
Для вершины V6:
d6+=1 d6-=2
Задача 3
Неориентированный граф
1. Построить матрицы смежности и инцидентности
2. Найти степени вершины графа
Матрица смежности
| V1 | V2 | V3 | V4 | V5 | V6 | |
| V1 | 0 | 1 | 1 | 0 | 1 | 1 |
| V2 | 1 | 0 | 0 | 0 | 1 | 0 |
| V3 | 1 | 0 | 0 | 1 | 0 | 0 |
| V4 | 0 | 0 | 1 | 0 | 1 | 0 |
| V5 | 1 | 1 | 0 | 1 | 0 | 1 |
| V6 | 1 | 0 | 0 | 0 | 1 | 0 |
Матрица инцидентности
| U1 | U2 | U3 | U4 | U5 | U6 | U7 | U8 | |
| V1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 |
| V2 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| V3 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
| V4 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| V5 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 |
| V6 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
Степень вершины неориентированного графа. Число рёбер, принадлежащие вершине.
d1=4 d4=2
d2=2 d5=4
d3=2 d6=2
Задача о кратчайшем пути
Пусть задана сеть из n+ 1 вершин, то есть ориентированный граф. В нем выделены две вершины – вход (нулевая вершина) и выход (вершина с номером n). Для каждой дуги заданы числа, называемые длинами дуг. Длиной пути (контура) называется сумма длин входящих в него дуг (если длины дуг не заданы, то длина пути (контура) определяется как число входящих в него дуг).
Задача заключается в поиске кратчайшего пути (пути минимальной длины) от входа до выхода сети. Будем предполагать, что в любую вершину сети можно попасть из входа и из любой вершины можно попасть в выход (вершины, не удовлетворяющие этому требованию, можно удалить). Известно, что для существования кратчайшего пути необходимо и достаточно отсутствия в сети контуров отрицательной длины. Номер строки в матрице соответствует номеру исходящей вершины, а номер столбца – входящей. Единица на пересечении i-й строки и j-го столбца ставится в том случае, если есть путь, выходящий из i-й вершины и входящий в j-ю. Во все остальные ячейки матрицы заносятся нули.
Найти кратчайший путь в сети, имеющей правильную нумерацию:
0) λ 0=0
Lik=gy:gy(r) Помечаем вершину индексом λ 0=0
1) λ 1=0
λ 1= λ 0 + L01=0+3= 3
Помечаем вершину индексом λ 1=3
2) λ 2 = min(λ 1 + L02 : λ 1 + L12)= min(0+9: 3+5)=8
Помечаем вершину индексом λ 2=8
3) λ 3= min(λ 1 + L13: λ 2 + L23) = min(3+8: 8+2)=10
Помечаем вершину индексом λ 3=10
4) λ 4= λ2+L24=8+1=9
Помечаем вершину индексом λ4=9
5) λ 5=min(λ3 + L35: λ 4+ L45)=min(10+4: 9+6)=14
Отсюда следует, что длина кратчайшего пути = 14
Методом обратного хода находится кратчайший путь. Если разность между индексом конечной вершины (дуги) и индексом начальной вершины (дуги) равен длине дуги, то длина входит в кратчайший путь.
λ 5- λ3 =14-10=4
L35=4, входит в кратчайший путь
λ 5- λ4=14-9=5
L46 не равно 5, не входит в кратчайший путь
λ 3 – λ1=10-3=7
L13 не равно 7, не входит в кратчайший путь
λ 3- λ2=10-8=2
L23=2, входит в кратчайший путь
λ 2- λ1=8-3=5
L12=5, входит в кратчайший путь
λ 1- λ0=3-0=3
L10=3, Водит в кратчайший путь
Следовательно кратчайший путь M:
0->1->2->3->5
Lm=14
Задача 4
Ориентированный граф
1. Построить матрицы, смежности, инцидентности.
2. Найти полустепени исхода и захода вершины.
Матрица смежности
Матрица смежности графа G с конечным числом вершин n (пронумерованных числами от 1 до n) — это квадратная матрица A размера n, в которой значение элемента aij равно числу рёбер из i-й вершины графа в j-ю вершину.
| V1 | V2 | V3 | V4 | V5 | |
| V1 | 1 | 1 | 0 | 0 | 0 |
| V2 | 0 | 0 | 1 | 1 | 1 |
| V3 | 1 | 0 | 0 | 0 | 1 |
| V4 | 0 | 0 | 0 | 1 | 0 |
| V5 | 0 | 0 | 0 | 0 | 0 |
Матрица инцидентности
| U1 | U2 | U3 | U4 | U5 | U6 | U7 | |
| V1 | 0 | 0 | 0 | -1 | -1 | 0 | 1 |
| V2 | 0 | 1 | 0 | 1 | 0 | 1 | -1 |
| V3 | 1 | 0 | 0 | -1 | 1 | -1 | 0 |
| V4 | 0 | 0 | -1 | 1 | 1 | 0 | 0 |
| V5 | -1 | -1 | 0 | -0 | 0 | 0 | 0 |
Найдём степени полуисхода и полузахода
Полустепенью исхода (захода) вершины 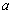графа 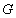будем называть число 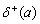(соответственно 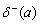), равное количеству дуг графа, исходящих из вершины 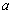(заходящих в вершину 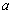). Вклад каждой петли, инцидентной вершине 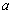, равен 1 как в 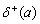, так и в .
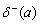Задача 2
Определим полустепени исхода и захода вершины данного графа:
Для вершины V1:
d1+=1, d1- =2
Для вершины V2:
d2+=3, d2-=1
Для вершины V3:
d3+=2, d3-=2
Для вершины V4:
d4+=2 d4-=1
Для вершины V5:
d5+=0 d5-=2
Задача 5
Неориентированный граф
3. Построить матрицы смежности и инцидентности
4. Найти степени вершины графа
Матрица смежности
| V1 | V2 | V3 | V4 | V5 | |
| V1 | 0 | 1 | 1 | 1 | 0 |
| V2 | 1 | 0 | 1 | 1 | 1 |
| V3 | 1 | 1 | 0 | 1 | 1 |
| V4 | 1 | 1 | 1 | 0 | 0 |
| V5 | 0 | 1 | 1 | 0 | 0 |
Матрица инцидентности
| U1 | U2 | U3 | U4 | U5 | U6 | U7 | |
| V1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 |
| V2 | 0 | 1 | 0 | 0 | 1 | 1 | 1 |
| V3 | 1 | 0 | 1 | 0 | 1 | 1 | 0 |
| V4 | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| V5 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
Степень вершины неориентированного графа. Число рёбер, принадлежащие вершине.
d1=3 d4=3
d2=4 d5=2
d3=4
Задача о кратчайшем пути
Пусть задана сеть из n+ 1 вершин, то есть ориентированный граф. В нем выделены две вершины – вход (нулевая вершина) и выход (вершина с номером n). Для каждой дуги заданы числа, называемые длинами дуг. Длиной пути (контура) называется сумма длин входящих в него дуг (если длины дуг не заданы, то длина пути (контура) определяется как число входящих в него дуг).
Задача заключается в поиске кратчайшего пути (пути минимальной длины) от входа до выхода сети. Будем предполагать, что в любую вершину сети можно попасть из входа и из любой вершины можно попасть в выход (вершины, не удовлетворяющие этому требованию, можно удалить). Известно, что для существования кратчайшего пути необходимо и достаточно отсутствия в сети контуров отрицательной длины. Номер строки в матрице соответствует номеру исходящей вершины, а номер столбца – входящей. Единица на пересечении i-й строки и j-го столбца ставится в том случае, если есть путь, выходящий из i-й вершины и входящий в j-ю. Во все остальные ячейки матрицы заносятся нули.
Найти кратчайший путь в сети, имеющей правильную нумерацию:
0) λ 0=0
Lik=gy:gy(r) Помечаем вершину индексом λ 0=0
1) λ 1=0
λ 1= λ 0 + L01=0+3= 3
Помечаем вершину индексом λ 1=3
2) λ 2 = λ 1 + L01= 3+6=9
Помечаем вершину индексом λ 2=9
3) λ 3= λ 3 + L34=9+3=12
Помечаем вершину индексом λ 3=12
4) λ 4= λ2+L45=12+3=15
Помечаем вершину индексом λ4=9
5) λ 5=min(λ5 + L56: λ 5+ L57)=min(15+1: 15+5)=16
Отсюда следует, что длина кратчайшего пути = 16
6) λ 6=min(λ6 + L78: λ 6+ L79)=min(16+7: 16+2)=18
Отсюда следует, что длина кратчайшего пути = 18
7) λ 7= λ6+L69=18+4=22
Помечаем вершину индексом λ 7=22
8) λ 8= λ2+L26=5+22=27
Помечаем вершину индексом λ 8=27
9) λ 9= λ9+L02=0+27=27
Помечаем вершину индексом λ 9=27
Методом обратного хода находится кратчайший путь. Если разность между индексом конечной вершины (дуги) и индексом начальной вершины (дуги) равен длине дуги, то длина входит в кратчайший путь.
λ 2- λ6 =27-22=5
L62=5, входит в кратчайший путь
λ 6- λ9=22-18=4
L96=4, входит в кратчайший путь
λ 9 – λ7=18-16=2
L79=2, входит в кратчайший путь
λ 7- λ5=16-15=1
L75 не равно 1, не входит в кратчайший путь
λ 5- λ4=15-12=3
L45=3, входит в кратчайший путь
λ 1- λ0=3-0=3
L10=3, Водит в кратчайший путь
Следовательно кратчайший путь M:
0->5->4->2->1->3
Lm=27