Абсолютная и относительная плотность жидкости
ГИДРОМЕХАНИКА БИЛЕТЫ
1. Основные парадигмы курса.
o Основы технической гидромеханики:
- гидростатика (это раздел гидравлики, в котором изучаются законы покоя жидкости, действующие при этом силы, плавание тел без их перемещения.)
- гидродинамика (это раздел механики жидкости (гидромеханики), изучающий движение жидкости, а также взаимодействие между жидкостью и твердыми телами при их относительном движении.)
- уравнения энергии
- системы водоснабжения и водоотведения
o Транспортирование жидкостей и газов:
- насосные установки
- вентиляторные установки
- компрессорные установки
· Основные вопросы гидравлики и аэродинамики систем водоснабжения и водоотведения.
Аэродинамика – это раздел гидродинамики, изучающий законы движения газообразной среды и ее взаимодействия с движущимися в ней твердыми телами. Основными задачами аэродинамики являются:
– определение сил, действующих на обтекаемое газом тело;
– распределение давления на поверхность тела;
– распределение скоростей в газе, обтекающем тело.
· Законы равновесия, основы кинематики и динамики, гидравлических сопротивлений при движении жидкости и газа.
· Обтекание потоком жидкости твердых тел.
· Механизмы перемешивания затопленных струй с окружающей средой и смешения сточных вод с водой водоемов.
· Основные элементы гидравлических машин и воздуходувных станций.
2. Классификация методов гидравлических исследований.
Методы
При решении практических вопросов гидравлика оперирует всеми известными методами исследований: методом анализа бесконечно малых величин, методом средних величин, методом анализа размерностей, методом аналогий, экспериментальным методом.
Метод анализа бесконечно малых величин - наиболее удобный из всех методов для количественного описания процессов равновесия и движения жидкостей и газов. Этот метод наиболее эффективен в тех случаях, когда приходится рассматривать движение объектов на атомно-молекулярном уровне, т.е. в тех случаях, когда для вывода уравнений движения приходится рассматривать жидкость (или газ) с молекулярно-кинетической теории строения вещества. Основной недостаток метода - довольно высокий уровень абстракции, что требует от читателя обширных знаний в области теоретической физики и умение пользоваться различными методами математического анализа, включая векторный анализ.
Метод средних величин - является более доступным методом, поскольку его основные положения базируется на простых (близких к обыденным) представлениях о строении вещества. При этом выводы основных уравнений в большинстве случаев не требуют знаний молекулярно-кинетической теории, а результаты, полученные при исследованиях, этим методом не противоречат «здравому смыслу» и кажутся обоснованными. Недостаток этого метода исследований связан с необходимостью иметь некоторые априорные представления о предмете исследований.
Метод анализа размерностей может рассматриваться в качестве одного из дополнительных методов исследований и предполагает всестороннее знания изучаемых физических процессов.
Методом аналогий - используется в тех случаях, кода имеются в наличии детально изученные процессы, относящиеся к тому же типу взаимодействия вещества, что и изучаемый процесс.
Экспериментальный метод - является основным методом изучения, если другие методы по каким- либо причинам не могут быть применены. Этот метод также часто используется как критерий для подтверждения правильности результатов, полученных другими методами.
В конечном счёте, метод изучения движения жидкости, а также уровень изучения (макро или микро) выбирается из условий практической постановки задач и соотношения характерных размеров.
3. Идеальная жидкость. Параметры и применение модели идеальной жидкости.
Идеальная жидкость в отличие от реальной жидкости не обладает внутренним трением, а также трением о стенки сосудов и трубопроводов, по которым она движется. Идеальная жидкость также обладает абсолютной несжимаемостью. Такая жидкость не существует в действительности, и была придумана для облегчения и упрощения ряда теоретических выводов и исследований.
Применение
Моделью идеальной жидкости пользуются при теоретическом рассмотрении задач, в которых вязкость не является определяющим фактором и ею можно пренебречь. В частности, такая идеализация допустима во многих случаях течения, рассматриваемых гидроаэромеханикой, и даёт хорошее описание реальных течений жидкостей и газов на достаточном удалении от омываемых твёрдых поверхностей и поверхностей раздела с неподвижной средой. Математическое описание течений идеальных жидкостей позволяет найти теоретическое решение ряда задач о движении жидкостей и газов в каналах различной формы, при истечении струй и при обтекании тел.
Параметры
4. Реальная жидкость и ее модель.
Реальная жидкость - жидкость, которая не обладает в совершенстве свойствами идеальной жидкости, она в некоторой степени сопротивляется касательным и растягивающим усилиям, а также отчасти сжимается. Для решения многих задач гидравлики этим отличием в свойствах идеальной и реальной жидкостей можно пренебречь. В связи с этим физические законы, выведенные для идеальной жидкости, могут быть применены к жидкостям реальным с соответствующими поправками.
5. Параметры состояния жидкости: абсолютное давление, абсолютная температура, плотность, относительная плотность.
Абсолютная и относительная плотность жидкости
Важнейшим физическим свойством жидкости, определяющим её концентрацию в пространстве, является плотность жидкости. Под плотностью жидкости понимается масса единицы объёма жидкости:
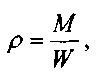
где: М - масса жидкости,
W - объём, занимаемый жидкостью.
Исключительными особенностями обладает вода, максимальная плотность которой отмечается при 4 °С
Кроме абсолютной величины плотности капельной жидкости, на практике пользуются и величиной её относительной плотности, которая представляет собой отношение величины абсолютной плотности жидкости к плотности чистой воды при температуре 4 °С:
.
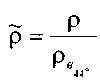Относительная плотность жидкости - величина безразмерная.
Абсолю́тное давле́ние ─ это истинное давление сплошных масс (жидкостей, паров и газов), отсчитываемое от абсолютного нуля давления ─ абсолютного вакуума. Абсолютный нуль давления макроскопических объёмов вещества практически недостижим, так как любое твёрдое тело образует пары, да и космическое пространство также не представляет собой абсолютную пустоту, лишённую вещества, поскольку содержит водород в количестве нескольких молекул на кубический сантиметр.
Шкала Кельвина (или абсолютная температурная шкала) – шкала, в которой температура замерзания воды принята равной 273,15 K, а температура ее кипения – 373,15 K. На практике часто используют приближенные значения: 273 и 373. Температуру, отсчитываемую по абсолютной шкале, называют абсолютной. Температуру, равную 0 К, называют абсолютным нулем.
6. Статические параметры жидкости. См. билет 5
Статическими называются параметры (давление, температура и другие) в потоке, движущемся с некоторой скоростью С. Чтобы точно измерить статические параметры, измерительные приборы должны перемещаться в потоке с одинаковой с ним скоростью.
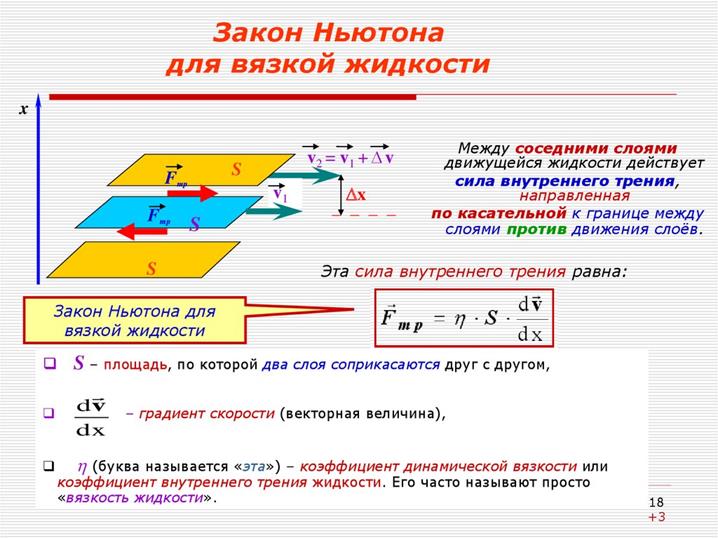
7. Силы, действующие в жидкости. Кинематическая и динамическая вязкость.
На произвольно выделенный объем жидкости действуют два вида сил:
Поверхностные – силы давления на свободной поверхности жидкости (атмосферное или отличное от него внешнее давление в замкнутом сосуде или силы давления соседних частит жидкости). Поверхностные силы распределены по поверхности и пропорциональны ее площади.
Р – сила давления
Т – сила трения
Массовые — объемные силы, пропорциональные массе жидкости: силы тяжести и инерционные силы
G – сила тяжести
I – сила инерции
Массовые силы действуют по всему выделенному объему и пропорциональны его массе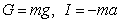 
. Поверхностные силы действуют по поверхности и пропорциональны площади поверхности.
Вязкость жидкости – это свойство реальных жидкостей оказывать сопротивление касательным усилиям (внутреннему трению) в потоке. Вязкость жидкости не может быть обнаружена при покое жидкости, так как она проявляется только при её движении.
Динамическая вязкость m. Единицей измерения этой вязкости является паскаль в секунду (Па*с). Физический смысл состоит в снижении давления в единицу времени. Динамическая вязкость характеризует сопротивление жидкости (или газа) смещению одного слоя относительно другого.
Динамическая вязкость зависит от температуры. Она уменьшается при повышении температуры и увеличивается при повышении давления.
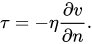
dv/dn – градиент скорости, т.е. отношение приращения скорости на границах слоя жидкости к его толщине
h - коэффициент вязкости, динамическая вязкость
Кинематическая вязкость n. Единицей измерения является Стокс. Кинематическая вязкость получается, как отношение динамической вязкости к плотности конкретного вещества.
Определение кинематической вязкости производится в классическом случае измерением времени вытекания определенного объема жидкости через калиброванное отверстие при воздействии силы тяжести.
8. Основные гипотезы гидромеханики.
В основе классической гидромеханики лежат следующие положения (гипотезы).
1. Справедливость классической механики Ньютона. Исследуются движения, когда скорости малы по сравнению со скоростью света, поэтому не надо пользоваться релятивисткой механикой. Рассматриваются объекты большие, чем объекты микромира, изучаемые квантовой механикой.
2. Справедливость классической термодинамики. Термодинамическим равновесным состоянием системы называется такое, в котором все характеристики внутреннего состояния замкнутой системы могут сколь угодно долго сохранять свои значения при сохранении внешних условий. В условиях термодинамического равновесия состояние жидкости можно определить с помощью нескольких макроскопических параметров (плотности, давления, температуры, скорости).
3. Справедливость схемы сплошной среды. В гидромеханике рассматриваются макроскопические движения жидкостей. При этом размеры рассматриваемых объектов жидкости и твердых тел оказываются не сопоставимо большими по сравнению с размерами молекул и межмолекулярным расстоянием Rмолек ≈ 10-9 ÷10-10 м, а длина свободного пробега молекулы ℓпробега ≈ 10-7 м = f(p,T). Указанные обстоятельства позволяют ввести гипотезу сплошности жидкости и рассматривать ее как материальную среду, масса которой непрерывно (сплошным образом) распределена по объему, т.е. отвлекаясь от молекулярного строения, представлять жидкость как непрерывно распределенную (размазанную) по пространству среду, обладающую физическими свойствами реальной жидкости. Исключения составляют сильноразреженные газы.
9. Допущения, рассматриваемые в гидромеханике жидкостей и газов.
В технической механике жидкости (гидравлике) при решении различных практических задач широко используются те или иные допущения и предположения, упрощающие рассматриваемый вопрос. Достаточно часто гидравлические решения основываются на результатах экспериментов, и потому в технической механике жидкости приводят относительно много различных эмпирических и полуэмпирических формул. При этом стремятся к оценке только главных характеристик изучаемого явления и часто
оперируют теми или иными интегральными и осредненными величинами, которые дают достаточную для технических приложений характеристику рассматриваемых явлений.
Например, в технической механике жидкости часто пользуются понятием средней скорости движения жидкости в том или другом поперечном сечении потока. По своему характеру техническая механика близка к известным дисциплинам – строительной механике и сопротивлению материалов, в которых под тем же углом зрения изучаются
вопросы механики твердого тела. Следует учитывать, что гидравлика, являясь общетехнической дисциплиной, должна рассматриваться как «профессиональная физика жидкого тела», в которой, в частности, даются основы соответствующих гидромеханических расчетов, используемых при проектировании инженерных сооружений, конструкций, а также надлежащих технологических процессов.
10. Методы Лагранжа и Ньютона.
Метод Лагранжа. Метод Лагранжа основан на исследовании движения отдельных частиц жидкости при их перемещении в пространстве.
В методе Лагранжа положение индивидуальной частицы описывается законом её движения, т.е. тремя уравнениями
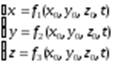; (3.1)
где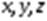 
- координаты частицы; 
- время; 
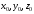- начальные координаты частиц, т.е. положение частиц в начальный момент времени. Следовательно, текущие координаты некоторой движущейся частицы 
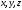являются функциями четырёх переменных 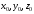и .Эти переменные называют переменными Лагранжа.
Совместное решение уравнений (3.1) определяет траекторию MN конкретной частицы с начальными координатами 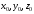в течение времени 
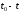(рис. 3.1).
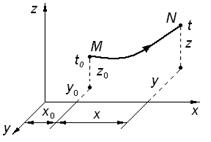
Рис. 3.1. Траектория частицы жидкости
Из теоретической механики известно, что первые производные этих функций по времени определяют компоненты скорости частицы жидкости:
; 
; 
,
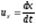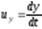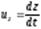а вторые производные – ускорения:
; 
; 
,
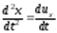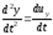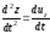где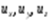 
- компоненты вектора скорости 
.
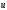Таким образом, в методе Лагранжа исследованию подлежит движение отдельных частиц жидкости.
Метод Ньютона
