Тема 9. Методи обробки експериментальних даних
Приклад 9.1. Підібрати емпіричну функцію для залежності між зростом і масою 10 юнаків-студентів, поданої таблицею:
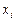
| 167 | 170 | 176 | 178 | 179 | 180 | 181 | 183 | 184 | 185 |
| 69 | 70 | 73 | 78 | 79 | 83 | 84 | 85 | 86 | 88 |
Оцінити розбіжності між емпіричними і теоретичними (обчисленими за емпіричною функцією) даними.
Розв’язання. Виберемо і побудуємо емпіричну функцію для залежності між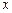 
(зростом) та 
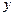(масою) юнаків. Для зручності проведемо відповідні обчислення і занесемо їх в таблицю 9.2.
Таблиця 9.2.
| № п/п | Емпірична функція |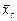 
| 
| 
| 
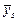
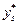
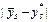
| Висновок |
| 1 | 
| 176,00 | 78,50 | 76,00 | 2,50 | мало придатна |
| 2 |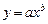 
| 175,77 | 77,92 | 72,89 | 5,04 | не придатна |
| 3 |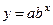 
| 176,00 | 77,92 | 76,00 | 1,92 | мало придатна |
| 4 |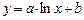 
| 175,77 | 78,50 | 72,89 | 5,62 | не придатна |
| 5 |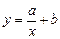 
| 175,54 | 78,50 | 72,77 | 5,73 | не придатна |
| 6 |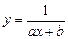 
| 176,00 | 77,35 | 76,00 | 1,35 | найбільш придатна |
| 7 |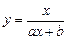 
| 175,54 | 77,35 | 72,77 | 4,58 | не придатна |
Тут значення 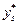знаходимо за формулою лінійної інтерполяції (9.10). Таблиця 9.2 показує, що для апроксимації вихідних даних найбільш придатна функція 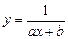. Ввівши нову змінну 
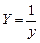, зведемо її до лінійної 
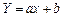. Проміжні обчислення помістимо в таблицю 9.3.
Таблиця 9.3.
| № п/п |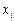 
| 
| 
| 
| 
| 
| 
|
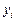
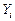
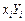
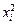
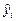
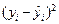
| 1 | 167 | 69 | 0,0145 | 2,4203 | 27889 | 67,6385 | 1,8537 |
| 2 | 170 | 70 | 0,0143 | 2,4286 | 28900 | 70,3127 | 0,0978 |
| 3 | 176 | 73 | 0,0137 | 2,4110 | 30976 | 76,3499 | 11,2217 |
| 4 | 178 | 78 | 0,0128 | 2,2821 | 31684 | 78,5995 | 0,3594 |
| 5 | 179 | 79 | 0,0127 | 2,2658 | 32041 | 79,7747 | 0,6002 |
| 6 | 180 | 83 | 0,0120 | 2,1687 | 32400 | 80,9856 | 4,0577 |
| 7 | 181 | 84 | 0,0119 | 2,1548 | 32761 | 82,2339 | 3,1192 |
Продовження табл. 9.3.
| 8 | 183 | 85 | 0,0118 | 2,1529 | 33489 | 84,8495 | 0,0227 |
| 9 | 184 | 86 | 0,0116 | 2,1395 | 33856 | 86,2207 | 0,0487 |
| 10 | 185 | 88 | 0,0114 | 2,1023 | 34225 | 87,6370 | 0,1318 |
| 1783 | 0,1267 | 22,5259 | 318221 | 21,5128 |
Cистема нормальних рівнянь у цьому випадку має вигляд:
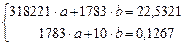
Коефіцієнти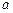 
і 
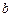цієї системи обчислюємо за формулами (9.5) і (9.6). Маємо
,
.
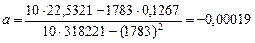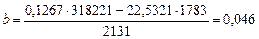Отже, шукана емпірична функція має вигляд:
.
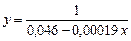Для оцінки розбіжності між емпіричними 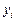і теоретичними 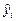даними, розрахованими за емпіричною функцією
.
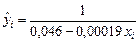підрахуємо суму квадратів відхилень (розрахунки наведені у таблиці 9.3, стовпчики 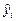і ):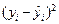
.
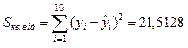Досить мале значення суми квадратів відхилень вказує на те, що емпірична функція добре апроксимує початкові дані.
Крім цього побудуємо графік емпіричної функції (рис.9.7), і на ньому відмітимо точками емпіричні значення.
Тема 9. Методи обробки експериментальних даних
Завдання 9. Підібрати емпіричну функцію для залежності між 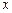та 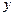, поданої таблицею. Оцінити розбіжность між емпіричними і теоретичними (обчисленими за емпіричною функцією) даними.
Варіанти завдань
| Варіант | 1 | 2 | 3 | 4 | 5 | 6 | |
|
|
|
|
|
|
|
|
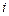
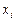
| 1 | 0,7 | 2,4 | 3,0 | 0,3 | -0,8 | 7,0 | -2,0 |
| 2 | 0,9 | 2,7 | 3,5 | 0,4 | 0,6 | 4,1 | 10,0 |
| 3 | 1,1 | 2,9 | 4,1 | 0,5 | 1,6 | 2,6 | 1,42 |
| 4 | 1,3 | 3,1 | 4,8 | 0,6 | 2,4 | 1,5 | 0,76 |
| 5 | 1,5 | 3,3 | 5,6 | 0,7 | 3,0 | 0,8 | 0,52 |
| 6 | 1,7 | 3,4 | 6,5 | 0,9 | 3,6 | 0,3 | 0,4 |
| 7 | 1,9 | 3,6 | 7,6 | 1,1 | 4,1 | -0,1 | 0,32 |
| 8 | 2,1 | 3,8 | 8,9 | 1,3 | 4,6 | -0,4 | 0,27 |
| 9 | 2,3 | 3,9 | 10,0 | 1,6 | 5,0 | -0,6 | 0,23 |
| 10 | 2,5 | 4,0 | 12,3 | 2,0 | 5,3 | -0,8 | 0,2 |
| Варіант | 7 | 8 | 9 | 10 | 11 | 12 | |
|
|
|
|
|
|
|
|
|
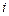
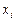
| 1 | 1,0 | 1,0 | 6,0 | 0,5 | 0,7 | 2,0 | 7,0 |
| 2 | 1,2 | 1,05 | 6,8 | 0,5 | 0,7 | 2,5 | 6,5 |
| 3 | 1,4 | 1,09 | 7,5 | 0,6 | 0,8 | 3,0 | 6,14 |
| 4 | 1,6 | 1,12 | 8,1 | 0,6 | 0,9 | 3,4 | 5,87 |
| 5 | 1,8 | 1,15 | 8,7 | 0,7 | 1,0 | 3,8 | 5,66 |
| 6 | 2,0 | 1,17 | 9,3 | 0,8 | 1,1 | 4,1 | 5,5 |
| 7 | 2,2 | 1,19 | 9,9 | 0,8 | 1,2 | 4,4 | 5,36 |
| 8 | 2,4 | 1,21 | 10,4 | 0,9 | 1,3 | 4,6 | 5,25 |
| 9 | 2,6 | 1,22 | 10,9 | 1,0 | 1,5 | 4,9 | 5,15 |
| 10 | 2,8 | 1,23 | 11,4 | 1,1 | 1,6 | 5,1 | 5,07 |
| Варіант | 1 3 | 14 | 15 | 16 | 17 | 18 | |
|
|
|
|
|
|
|
|
|
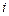
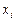
| 1 | 1,0 | 3,0 | 4,4 | 0,3 | -0,8 | 8,0 | 1,0 |
| 2 | 1,3 | 3,3 | 5,6 | 0,4 | 0,3 | 6,8 | 0,52 |
| 3 | 1,6 | 3,5 | 7,1 | 0,4 | 1,1 | 6,1 | 0,35 |
| 4 | 1,9 | 3,8 | 8,9 | 0,5 | 1,8 | 5,6 | 0,27 |
| 5 | 2,2 | 4,0 | 11,3 | 0,6 | 2,4 | 5,3 | 0,21 |
| 6 | 2,5 | 4,2 | 14,4 | 0,7 | 2,9 | 5,0 | 0,18 |
| 7 | 2,8 | 4,3 | 18,2 | 0,8 | 3,3 | 4,8 | 0,15 |
| 8 | 3,1 | 4,5 | 23,0 | 0,9 | 3,8 | 4,6 | 0,13 |
| 9 | 3,4 | 4,7 | 29,2 | 1,1 | 4,1 | 4,5 | 0,12 |
| 10 | 3,7 | 4,8 | 37,0 | 1,3 | 4,5 | 4,4 | 0,11 |
| Варіант | 1 9 | 2 0 | 21 | 22 | 23 | 24 | |
|
|
|
|
|
|
|
|
|
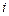
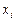
| 1 | 2,0 | 1,17 | 9,3 | 0,6 | 0,9 | 3,7 | 5,5 |
| 2 | 2,5 | 1,22 | 10,6 | 0,7 | 1,1 | 4,8 | 5,2 |
| 3 | 3,0 | 1,25 | 11,9 | 0,8 | 1,2 | 5,7 | 5,0 |
| 4 | 3,5 | 1,27 | 13,0 | 1,0 | 1,4 | 6,5 | 4,85 |
| 5 | 4,0 | 1,29 | 14,0 | 1,2 | 1,7 | 7,1 | 4,75 |
| 6 | 4,5 | 1,30 | 15,0 | 1,4 | 1,9 | 7,7 | 4,66 |
| 7 | 5,0 | 1,31 | 15,9 | 1,6 | 2,2 | 8,3 | 4,6 |
| 8 | 5,5 | 1,32 | 16,8 | 1,9 | 2,6 | 8,7 | 4,54 |
| 9 | 6,0 | 1,32 | 17,6 | 2,3 | 3,0 | 9,2 | 4,5 |
| 10 | 6,5 | 1,34 | 18,4 | 2,7 | 3,5 | 9,6 | 4,46 |
| Варіант | 25 | 2 6 | 27 | 28 | 29 | 30 | |
|
|
|
|
|
|
|
|
|
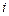
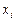
| 1 | 5,0 | 6,57 | 28,5 | 7,0 | 0,7 | 5,1 | 9,0 |
| 2 | 5,5 | 6,62 | 30,2 | 7,4 | 0,8 | 5,4 | 8,72 |
| 3 | 6,0 | 6,66 | 31,7 | 7,9 | 0,9 | 5,6 | 8,5 |
| 4 | 6,5 | 6,70 | 33,2 | 8,4 | 1,0 | 5,9 | 8,3 |
| 5 | 7,0 | 6,73 | 34,7 | 9,0 | 1,2 | 6,1 | 8,14 |
| 6 | 7,5 | 6,75 | 36,1 | 9,7 | 1,4 | 6,3 | 8,0 |
| 7 | 8,0 | 6,78 | 37,4 | 10,5 | 1,6 | 6,5 | 7,87 |
| 8 | 8,5 | 6,80 | 38,7 | 11,4 | 1,9 | 6,7 | 7,76 |
| 9 | 9,0 | 6,81 | 40,0 | 12,5 | 2,2 | 6,8 | 7,66 |
| 10 | 9,5 | 6,83 | 41,2 | 13,7 | 2,5 | 7,0 | 7,57 |