. За оптимальное значение степени многочлена следует принять то значение m, начиная с которого величина стабилизируется или начинает возрастать.
| Метод наименьших квадратов |
| Главная / Лабораторное оборудование / Приборы МУЛЬТИТЕСТ / Методы |
Общие положения
(см. рисунок). Требуется найти уравнение прямой
наилучшим образом согласующейся с опытными точками. Пусть мы нашли такую прямую. Обозначим через Из уравнения (2) следует, что
Чем меньше числа
Покажем, как можно подобрать прямую (2) так, чтобы сумма квадратов S была минимальной. Из уравнений (3) и (4) получаем
Условия минимума S будут
Уравнения (6) и (7) можно записать в таком виде:
Из уравнений (8) и (9) легко найти a и b по опытным значениям xi и yi. Прямая (2), определяемая уравнениями (8) и (9), называется прямой, полученной по методу наименьших квадратов (этим названием подчеркивается то, что сумма квадратов S имеет минимум). Уравнения (8) и (9), из которых определяется прямая (2), называются нормальными уравнениями. Можно указать простой и общий способ составления нормальных уравнений. Используя опытные точки (1) и уравнение (2), можно записать систему уравнений для a и b
Умножим левую и правую части каждого из этих уравнений на коэффициент при первой неизвестной a (т.е. на x1, x2, ..., xn) и сложим полученные уравнения, в результате получится первое нормальное уравнение (8). Умножим левую и правую части каждого из этих уравнений на коэффициент при второй неизвестной b, т.е. на 1, и сложим полученные уравнения, в результате получится второе нормальное уравнение (9). Этот способ получения нормальных уравнений является общим: он пригоден, например, и для функции
Естественно, что здесь получится система из n+1 нормального уравнения для определения величин Рассмотрим частный случай применения метода наименьших квадратов. Пусть из теории известно, что
есть величина постоянная и ее нужно определить по опытным данным (1). Систему уравнений для k можно записать:
Для получения нормального уравнения умножим каждое из этих уравнений на коэффициент при неизвестной k, т.е. на 1, и сложим полученные уравнения
отсюда
Следовательно, среднее арифметическое, полученное из опытных отношений yi/xi, дает решение поставленной задачи по методу наименьших квадратов. Это важное свойство средней арифметической объясняет ее широкое применение в практике обработки опытных данных. Пример 1 На опыте получены значения x и y, сведенные в таблицу
Найти прямую (2) по методу наименьших квадратов. Решение. Находим:
Записываем уравнения (8) и (9) |
Из Exponenta.ru
Теория
Постановка задачи приближения функции по методу наименьших квадратов ~ Нормальная система метода наименьших квадратов ~ Выбор степени аппроксимирующего многочлена
На практике часто возникает необходимость найти функциональную зависимость между величинами x и y, которые получены в результате эксперимента. Часто вид эмпирической зависимости известен, но числовые параметры неизвестны.
Ниже рассматривается решение задачи приближения многочленами таблично заданной функции по методу наименьших квадратов и по методу интерполяции.
Постановка задачи приближения функции по методу наименьших квадратов . Пусть функция y=f(x) задана таблицей своих значений: 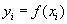 , i=0,1,-n. Требуется найти многочлен фиксированной степени m, для которого среднеквадратичное отклонение (СКО)
, i=0,1,-n. Требуется найти многочлен фиксированной степени m, для которого среднеквадратичное отклонение (СКО) 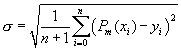 минимально.
минимально.
Так как многочлен 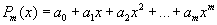 определяется своими коэффициентами, то фактически нужно подобрать набор кофициентов
определяется своими коэффициентами, то фактически нужно подобрать набор кофициентов 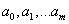 , минимизирующий функцию
, минимизирующий функцию 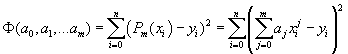 .
.
Используя необходимое условие экстремума, 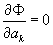 , k=0,1,-m получаем так называемую нормальную систему метода наименьших квадратов:
, k=0,1,-m получаем так называемую нормальную систему метода наименьших квадратов: 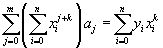 , k=0,1,-m.
, k=0,1,-m.
Полученная система есть система алгебраических уравнений относительно неизвестных 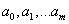 . Можно показать, что определитель этой системы отличен от нуля, то есть решение существует и единственно. Однако при высоких степенях m система является плохо обусловленной. Поэтому метод наименьших квадратов применяют для нахождения многочленов, степень которых не выше 5. Решение нормальной системы можно найти, например, методом Гаусса.
. Можно показать, что определитель этой системы отличен от нуля, то есть решение существует и единственно. Однако при высоких степенях m система является плохо обусловленной. Поэтому метод наименьших квадратов применяют для нахождения многочленов, степень которых не выше 5. Решение нормальной системы можно найти, например, методом Гаусса.
Запишем нормальную систему наименьших квадратов для двух простых случаев: m=0 и m=2. При m=0 многочлен примет вид: 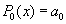 . Для нахождения неизвестного коэффициента
. Для нахождения неизвестного коэффициента 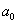 имеем уравнение:
имеем уравнение: 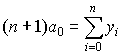 . Получаем, что коэффициент
. Получаем, что коэффициент 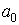 есть среднее арифметическое значений функции в заданных точках.
есть среднее арифметическое значений функции в заданных точках.
Если же используется многочлен второй степени 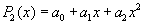 , то нормальная система уравнений примет вид:
, то нормальная система уравнений примет вид:
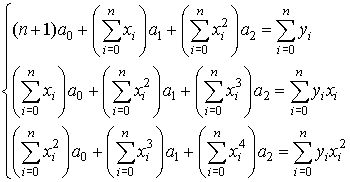

ПРИМЕР 1. Приближение функции по методу наименьших квадратов.
Предположим, что функцию f можно с высокой точностью аппроксимировать многочленом 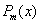 некоторой степени m. Если эта степень заранее неизвестна, то возникает проблема выбора оптимальной степени аппроксимирующего многочлена в условиях, когда исходные данные
некоторой степени m. Если эта степень заранее неизвестна, то возникает проблема выбора оптимальной степени аппроксимирующего многочлена в условиях, когда исходные данные 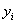 содержат случайные ошибки. Для решения этой задачи можно принять следующий алгоритм: для каждого m=0,1,2,.. вычисляется величина
содержат случайные ошибки. Для решения этой задачи можно принять следующий алгоритм: для каждого m=0,1,2,.. вычисляется величина
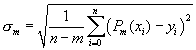 . За оптимальное значение степени многочлена следует принять то значение m, начиная с которого величина
. За оптимальное значение степени многочлена следует принять то значение m, начиная с которого величина 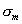 стабилизируется или начинает возрастать.
стабилизируется или начинает возрастать.
ПРИМЕР 2. Нахождение оптимальной степени многочлена.
Определение параметров эмпирической зависимости. Часто из физических соображений следует, что зависимость 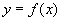 между величинами хорошо описывается моделью вида
между величинами хорошо описывается моделью вида 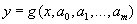 , где вид зависимости g известен. Тогда применение критерия наименьших квадратов приводит к задаче определения искомых параметров
, где вид зависимости g известен. Тогда применение критерия наименьших квадратов приводит к задаче определения искомых параметров 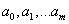 из условия минимума функции:
из условия минимума функции: 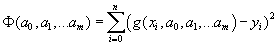 .
.

ПРИМЕР 3. Вывод нормальной системы уравнений для нахождения параметров эмпирической зависимости.
Если зависимость от параметров 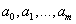 нелинейна, то экстремум функции
нелинейна, то экстремум функции 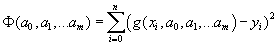 ищут методами минимизации функций нескольких переменных.
ищут методами минимизации функций нескольких переменных.
Пример 1. Приближение функции по методу наименьших квадратов.
Пусть функция задана таблицей своих значений:
| x | -3 | -1 | 0 | 1 | 3 |
| y | -4 | -0.8 | 1.6 | 2.3 | 1.5 |
Приблизим функцию многочленом 2-ой степени. Для этого вычислим коэффициенты нормальной системы уравнений:
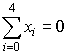 ,
, 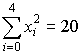 ,
, 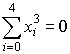 ,
, 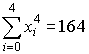
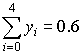 ,
, 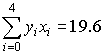 ,
, 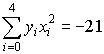
Составим нормальную систему наименьших квадратов, которая имеет вид:
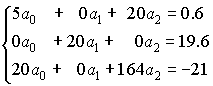
Решение системы легко находится: 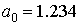 ,
, 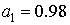 ,
, 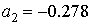 .
.
Таким образом, многочлен 2-ой степени найден: 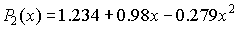 .
.
Теоретическая справка

Пример 2. Нахождение оптимальной степени многочлена.
| Решение примера в среде пакета Mathcad | 
| Теоретическая справка |
| Решение примера в среде пакета Mathematica | 
| |
| Решение примера в среде пакета Matlab | 
|

Пример 3. Вывод нормальной системы уравнений для нахождения параметров эмпирической зависимости.
Выведем систему уравнений для определения коэффициентов 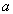 и
и 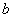 функции
функции 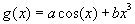 , осуществляющей среднеквадратичную аппроксимацию заданной функции
, осуществляющей среднеквадратичную аппроксимацию заданной функции  по
по 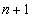 точкам. Составим функцию
точкам. Составим функцию 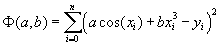 и запишем для нее необходимое условие экстремума:
и запишем для нее необходимое условие экстремума:
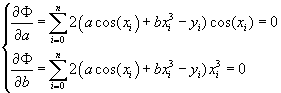
Тогда нормальная система примет вид:
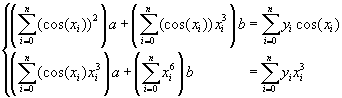
Получили линейную систему уравнений относительно неизвестных параметров и, которая легко решается.
Самостоятельно
Задача 1.
Построить приближение таблично заданной функции по методу наименьших квадратов многочленами 0-ой, 1-ой и 2-ой степеней.
| x | -2 | -1 | 0 | 1 | 2 |
| y | 9.9 | 5.1 | 1.9 | 1.1 | 1.9 |
Построить графики функции и найденных многочленов.
Задача 2.
Функция y=a/x+b задана таблицей своих значений.
| x | 0.1 | 0.2 | 0.5 |
| y | 10.22 | 5.14 | 2.76 |
Найти параметры a и b по методу наименьших квадратов Указание. Предварительно свести задачу к линейной, сделав замену: t=1/x. Тогда функция y приближается многочленом 1-ой степени a t+b.
Задача 3.
Вывести нормальную систему уравнений для определения параметров a, b, c функции g(x)=a sin(x)+b cos(x)+c , осуществляющей среднеквадратичную аппроксимацию таблично заданной функции y(x).









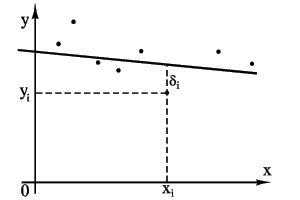
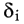 расстояние опытной точки от этой прямой (измеренное параллельно оси y).
расстояние опытной точки от этой прямой (измеренное параллельно оси y).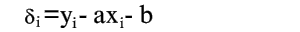
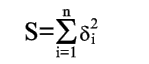
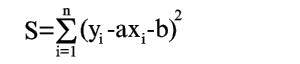
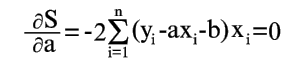
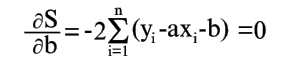
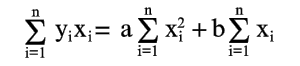
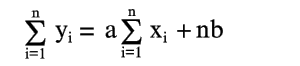
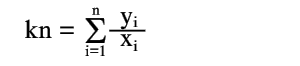
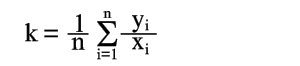
 xi=21,
xi=21,