2 раз. Необходимо показать учащимся, что пример у 3 можно про*

Дата: 2025-06-14; Просмотры: 1

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

2 2 I

читать по-разному: у умножить на 3, у увеличить в 3 раза, найти!

22 I

произведение у и 3; множители у и 3, найти произведение. После!

2 о 6 '

решения примера уЗ=у следует сравнить произведение и пер-

6 ' 2 ~ 2 6 ₀

выи множитель: у больше у в 3 раза, •=• меньше у в 3 раза.

Надо решать примеры и с неизвестным числителем или знаме­нателем в первом множителе вида: -~--2=-г, т=г-2=-я-.

Можно предложить и более трудные примеры вида:

. а , 4 1 ,-, 3 П г-, 2

¹ - а -⁴= Ъи ' ^а = Г > П'^П=5

2. Дробь тг увеличить в 3 раза.

Деление дроби на целое число дается в следующей последо­вательности:

1.Деление дроби на целое число без предварительного сокра­
щения.

2. Деление смешанного числа на целое число без предваритель­
ного сокращения.

3. Деление с предварительным сокращением.

Учащимся необходимо показать и такие случаи деления дроби или смешанного числа на целое, когда предварительное сокраще­ние облегчает процесс выполнения действия. Например:

4Ж2 315Ш5

5-²⁼7^-⁼5' ³4-^{9 =} Т"^{:9 =} 4^⁼Т2-

1 3

314

На основе наблюдений и конкретной деятельности учащиеся

н'мнодятся к выводу: при делении дроби на целое число доли

1.ПЮВЯТСЯ мельче, число же долей не изменяется. Например,

| гни взять половину яблока и разделить эту половину на 2 рав-

ц.к' части (-я- : 2 ] , то получится по -т яблока. Записываем: -к\2=-^.

Каждый ученик должен самостоятельно половину круга (полоски, Отрезки) разделить на 2 равные части и записать результат деле-

ния.

Далее рассматривается деление, например, -^ на 3 равные

2 2

Части: -^:3=к- Учащиеся видят, что получились при делении девя­тые доли, а число их не изменилось. Сравниваются числитель и знаменатель частного и делимого: знаменатель увеличился в 3 раза, а числитель не изменился. Отсюда можно сделать вывод: чтобы разделить дробь на целое число, нужно знаменатель умно­жить на это число, а числитель оставить тот же. На основе правила решается пример: 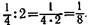Затем на предметах уча-

щиеся должны еще раз показать процесс деления и убедиться, что пример решен верно.

Деление дроби на целое число необходимо сопоставить с умно­жением дроби на целое число, решая взаимно обратные примеры вида 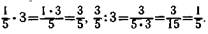При этом следует сравнить

произведение и частное соответственно с первым множителем и делимым. Это надо для того, чтобы учащихся подвести к обобще­нию: при умножении дроби на целое число произведение во столь­ко раз больше первого множителя, сколько единиц содержится во втором множителе. Аналогичный вывод нужно сделать и для част­ного.

Деление смешанного числа на целое дается по аналогии со вторым способом умножения смешанного числа на целое, напри­мер: 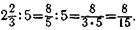Смешанное число обращается в непра-

вильную дробь и деление производится по правилу деления дроби на целое число.

Наиболее сильных учащихся нужно познакомить и с особыми случаями деления. Если целая часть смешанного числа нацело делится на делитель, то смешанное число не обращается в непра-

315

вильную дробь, например: 2-^'.2=\-^. Нужно делить сначала

часть, результат записать в частное, затем делить дробную част

2 22

правилу деления дроби на целое число: 12^:3=47^=4-^. В

случае деление смешанного числа нужно показать на предметиц пособиях. После изучения всех четырех действий с обыкновений ми дробями предлагаются сложные примеры со скобками и порядок действий.