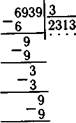2. Умножение и деление на однозначное число.
3. Умножение и деление на круглые десятки, сотни и тысячи.
4. Умножение и деление на двузначные и трехзначные числа:
а) умножение и деление двузначного числа на двузначное;
б) умножение и деление трехзначного числа на двузначное (в
частном число десятков равно сначала 1, а затем 2 и т. д.);
в) умножение и деление четырехзначного числа на двузначное
(число сотен в частном сначала равно 1, затем 2 и т. д.);
г) деление четырехзначного числа на двузначное, когда число
сотен в делимом меньше, чем в делителе, и т. д.
Для лучшей отработки приемов осуществления этих действий, их дифференцировки, установления взаимосвязи между действиями на каждом этапе изучения действий сначала отрабатываются приемы умножения, а затем деления, действия сопоставляются,
229
показывается их взаимосвязь. Учащиеся знакомятся также с п| веркой действий.
После первоначального знакомства с алгоритмом умножени» деления необходимо дать достаточное количество вариативных |_ ражнений, для того чтобы учащиеся научились применять его к различным числам. Затем учащиеся учатся закреплять алгоритм и разных ситуациях, сначала под руководством учителя, а потом и самостоятельно.
2. Умножение и деление разрядных чисел на ^позначное число начинается с повторения этих действий [уже известными учащимся числами — умножаются и делятся: ) десятки (30x3, 80x4, 90:3); б) сотни (700x2, 800:4). Затем рассматриваются устные случаи умножения и деления единиц тысяч: 3000-2, 9000:3. Действия с этими числами сопоставляют-| си с действиями над простыми единицами:
| 9:3=3 9 тыс.:3=3 тыс. |
3-2=6
3 тыс.-2=6 тыс.
| и деление разрядных 20 000:4 800 000:4 |
Умножение и деление многозначных чисел на однозначное число
Последовательность выполнения действий:
1. Подготовительные упражнения.
2. Умножение и деление разрядных чисел на однозначное
число.
3. Умножение и деление многозначных чисел на однозначные
без раздробления и превращения разрядных единиц (12 432x2,
69 396:3).
4. Умножение и деление многозначных чисел на однозначные с
раздроблением и превращением разрядных единиц сначала в
одном, а затем в двух и более разрядах (2743-2, 42 696:3).
5. Особые случаи умножения и деления, в которых нули стоят
в середине или на конце множимого (3840 «3), делимого
(75 048:3, 42 360:3) или получаются в частном (75 130:5).
1. Подготовительные упражнения необходимы для повторения и обобщения имеющихся знаний учащихся о действиях умножения и деления, а также для подготовки их к более сознательному восприятию нового материала.
Необходимо повторить с учащимися, что действие умножения — это нахождение суммы одинаковых слагаемых. Поэтому полезны упражнения на замену произведения суммой одинаковых слагаемых и наоборот:
8.3=8+8+8; 20+20+20+20=20-4.
Повторяется также табличное умножение и деление, умножение единицы и нуля (1x7, 29x1, 0x3, 43x0), деление единицы и нуля (1:1, 0:8), деление на единицу (17:1). Учащиеся вспоминают названия компонентов действий умножения и деления и их результатов.
230
Аналогично объясняется умножение чисел в пределах 100 000 и 1 000 000.
30 000 • 3 300 000 - 2
Приемами устных вычислений выполняются действия умножения и деления и над круглыми числами: 15 000:5, 12 000-2, 350 000:7, 24 000-2. Действия с числами указанных выше видов выполняются устно и включаются, как правило, на уроках математики в устный счет.
3. Умножение и деление многозначных чисел на однозначное число без раздробления и превращения не представляют собой ничего нового по сравнению с выполнением этих действий в пределах 1000. Поэтому эти действия также следует рассматривать как подготовительные к следующему, более трудному этапу. Нужно повторить, как подписываются числа при записи примеров в столбик, требовать подробных объяснений, затем объяснения свертываются (разрядные единицы не называются):
|
|
| 413 х 3 1239 |
..2243
* 2
4486
Далее учащиеся решают примеры на умножение, а затем и на деление с раздроблением и превращением разрядных единиц.
231
Умножение многозначного числа на однозначное
Подбираются для решения случаи с постепенным нарастание трудности: сначала с переходом через разряд в одном, в двух, затем и в нескольких разрядах.
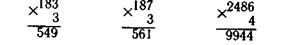
Наконец, решаются примеры на умножение, в которых первым множитель имеет нули в середине или на конце (особые случаи)
Опыт и специальные исследования показывают, что в условиях вспомогательной школы целесообразно бывает сохранить единую, привычную для учащихся форму записи умножения в столбик даже в том случае, когда первый множитель оканчивается нулями:
| ,24000 |
| X |
| X |
,24 080
168 000 120 400
При записи примеров с первым множителем, оканчивающимся! нулями, второй множитель можно подписывать под первой значащей цифрой справа:
,24000
| ,24 080 |
| ,2 408 тыс. |
.,24 тыс.
| X |
| X |
Х 7
| 168 000 |
| 12 040 дес. |
168 тыс. 120 400
Покажем объяснение случая 24 080 х 5. В числе 24 080 содер-, жится 2408 десятков. Умножаем их на 5, получаем 12 040 десятков или 120 400.
Такое объяснение оказывается доступным не всем, а только наиболее хорошо успевающим по математике умственно отсталым учащимся.
Учитель должен выбрать единый вычислительный прием, единую форму записи и пользоваться ими во всех случаях.
Деление многозначного числа на однозначное
При делении необходимо примеры подбирать так, чтобы высший разряд делимого делился на делитель (был больше его). На таких примерах удобнее всего закрепить предварительную прикидку числа цифр в частном, о которой учащиеся уже получили представление при делении чисел в пределах 1000. 232
I
Например, берем 5 тысяч и делим на 4, в частном получим
четырехзначное число.
| 5548 "4 | 4 |
| 1387 |
| 15 "12 |
Деля 5:4, в частном берем по 1, проверяем: 1x4=4. Из 5 вычитаем 4, остаток 1. Сносим сотни. Делим 15 сотен на 4. Берем по 3 и т. д. Частное 1387. Делим проверку: 1387x4.
| 34 "32 |
| 28 "28 |
Затем подбираются примеры, в которых высший разряд делимого не делится нацело на делитель 12 575:5 (один десяток тысяч не делится на 5). Тогда на 5 делим 12 единиц тысяч. В частном будет четырехзначное число. Ставим 4 точки в частном, начинаем делить 12 ед. тысяч на 5 и т. д. Необходимо работать в этот период над закреплением алгоритма деления. Чтобы ученики лучше запомнили последовательность рассуждений при выполнении этого действия, полезно использовать схему, в которой это подробно излагается: 1) прочитай и запиши пример; 2) выдели первое неполное делимое; 3) определи количество цифр в частном и поставь на их месте точки; 4) раздели неполное делимое и запиши полученное число в частное; 5) умножь это число на делитель, чтобы узнать, какое число ты разделил; 6) вычти, чтобы узнать, сколько еще единиц осталось разделить; остаток должен быть меньше делителя; 7) остаток вырази в единицах низшего разряда и прибавь к нему единицы такого же разряда делимого; 8) деление так же продолжай до полного решения примера; 9) сопоставь частное и делимое; частное должно быть меньше делимого; 10) проверь ответ действием
умножения.
Этой схемой учитель пользуется при объяснении деления, учит ею пользоваться учащихся. Сначала учащиеся читают по схеме каждое задание и отвечают. Затем задание читается ими про себя, а ответ произносится вслух. Наконец, учащиеся пользуются этой схемой самостоятельно, учитель может помогать учащимся лишь наводящими вопросами.
Особое внимание следует уделить таким случаям деления, в которых нули получаются в середине или на конце частного. Например: «Разделим 3840 на 4. 3 тысячи на 4 не делятся. Берем 38 сотен и делим их на 4. В частном получится трехзначное число. Поставим в частном 3 точки. 38 сотен разделим на 4, получим по 9 сотен. Умножим 9 сотен на 4, получим 36 сотен. От вычитания получим 2 сотни — это 20 десятков, 20 десятков да
233
еще 4 десятка, всего 24 десятка. Делим 24 десятка на 4. Возьмем по 6, умножим 6 на 4, получим 24. О единиц разделим на 4. получим 0.
|
|
| Т046~ |
| 355" |
Разделим 6276 на 6; 6 единиц тысяч будем делить на 6. Возьмем по 1. В частном получится четырехзначное число. Ставим 4 точки 1 ед. тыс. умножим на 6, получим 6. Проверим вычитанием, все ли тысячи разделились. Остатка нет. Делим 2 сотни на 6, 2 сотни не де лятся на 6, поэтому на месте сотен пишем в частном 0. 27 десятком делим на 6. Возьмем по 4». И т. д. При делении многозначного числл на однозначное рассматриваются и случаи деления с остатком, например 2487:7. Важно постоянно обращать внимание учащихся на то, что оста ток должен быть меньше делителя.
2 (ост.)