Методика изучения табличного умножения и деления
В практике работы школы VIII вида получила распространение 'дующая система изучения действий умножения и деления она требует глубокого научного обоснования и дополнитель-|Ых экспериментальных исследований):
1.Ознакомление с умножением как сложением одинаковых
!Лвгаемых.
2. Ознакомление с делением на равные части.
3. Составление таблицы умножения числа 2.
4. Составление таблицы деления на 2 (рассматривается толь-
Ко деление на равные части).
б. Составление таблицы умножения в пределах 20.
6. Составление таблицы деления в пределах 20 (деление на
равные части).
7. Практическое знакомство с переместительным законом ум
ножения.
8. Сопоставление умножения и деления как взаимно обратных
действий.
9. Изучение умножения и деления в пределах 100. Составле
ние таблиц умножения и деления. Практическое знакомство с
переместительным законом умножения.
10. Деление с остатком.
11.Деление по содержанию (практическое деление предметных
множеств).
12. Сопоставление деления на равные части и деления по
содержанию в практической деятельности и при решении простых
задач.
13. Умножение на единицу и единицы. Деление на единицу.
14. Нуль как компонент умножения. Нуль как делимое. ..)
При обучении умножению и делению перед учителем стоит
сложная задача — раскрыть смысл каждого арифметического действия на конкретном материале. Необходимо добиваться, чтобы на основе действий с конкретными предметами учащиеся смогли сделать доступные им выводы, обобщения, отдифференцировать действие умножения от сложения и в то же время установить связь, существующую между этими действиями, чтобы они осознали, что умножение — это сложение одинаковых слагаемых.
163
^"»
ОБУЧЕНИЕ ТАБЛИЧНОМУ УМНОЖЕНИЮ И ДЕЛЕНИЮ В ПРЕДЕЛАХ 20
Впервые в 3-м классе учащиеся школы VIII вида знакомятся < новыми арифметическими действиями умножением и делением, составляют, заучивают таблицы умножения и деления чисел 2, .1, 4, 5 с ответами, не превышающими число 20. Лучшему осознании' смысла действия умножения способствует подготовительная р та: счет равными группами предметов, а также счет по 2, 3, до 20, С этой целью учитель готовит наглядные пособия, разда ный Материал. Такими пособиями служат учебные принадлежи > ти, природный материал, игрушки, изображения предметов в вю<' трафаретов, разнообразные рисунки и т. д.
Причем желательно объединять предметы, которые встречай ся группами в жизненных условиях. Например, соединять варе ки, перчатки, носки в пары, яйца — в десятки, пальцы рук в группу по 5, колеса автомобиля — по 4, ножки табуретки — по 3 и т. д.
Например, учитель говорит:
— Ребята, вы будете кататься на лыжах. Каждому из вас
нужно надеть варежки. Сколько варежек нужно одному ученику?
Постройтесь у доски (учитель вызывает 5 человек). Пусть каждый
возьмет по паре варежек. Считаем вместе, хором, сколько всего
варежек взяли ученики: 2, 4, 6, 8, 10.
— За каждой партой в нашем классе сидят по 2 ученика.
Пересчитаем всех учеников в классе. Чтобы быстрее сосчитать,
будем считать по 2.
— Нужно сложить в корзину все яблоки и сосчитать, сколько
яблок в корзине. Чтобы быстро сосчитать, будем брать сразу по 2
яблока и считать: 2, 4, 6, .... 18, 20. Сколько всего яблок? Сколь
ко раз взяли по 2 яблока?
На этот вопрос ученики не могут ответить. Поэтому при счете парами других предметов надо, чтобы один ученик считал по 2, а другой — сколько раз взяли по два. К доске выходят 2 ученика. Первый ученик берет из коробки по 2 карандаша и считает: 2, 4, .... а второй считает, сколько раз первый ученик взял по 2 карандаша.
Счет ведется не только по 2, но и другими равными числовыми группами. Например, учитель ставит несколько игрушечных машин и дает детям задание: «Сосчитаем, сколько колес у этих машин. Сколько колес у одной машины? Как будем считать, чтобы быстро сосчитать колеса у всех машин: по 1 или по 4?» «4, 8, 164
|», — считают дети. «Если будет еще одна машина, то сколько пес еще надо прибавить?» Следует спросить у детей, какие едметы удобно считать парами, по 5, по 10. Если ученики не дут ответа на этот вопрос, то учитель должен ответить сам.
Ученикам предлагается задача:
«Девочка собрала цветы и поставила их в 3 вазочки по 5 штук. |осчитаем, сколько цветов собрала девочка (на наборном полотне вставлена табличка с рисунками ваз)». Дети считают: 5, 10, 15.
Затем учитель просит по этому рисунку составить пример: 5+5+5=15. Для этого он выставляет числовые фигуры, по которым учащиеся должны самостоятельно составить пример и решить его.
В этот период полезно работать с дидактическим материалом. Сначала учащиеся отсчитывают равные группы предметов, а потом и таблички с изображением равных групп предметов. Например, при счете по 3 они берут в руку каждый раз по 3 палочки (кружочка).
Можно дать также задания: раскрасить клеточки тетради или обвести по 2, по 3 клеточки; нарисовать круги, палочки, треугольники по 2, по 3, по 4, по 5 или раскрасить готовые; составить рисунки к примерам вида 3+3+3=9; по карточкам и по рисункам составить таблички сложения; составить примеры на сложение по рисунку.
Для счета равными группами используются одинаковые монеты.
Подобные упражнения, проводящиеся систематически, подготовят учащихся к запоминанию по существу ответов табличного умножения в пределах 20.
Понятие об умножении как сложении равных слагаемых учащиеся получают на первом уроке. Необходимо показать целесообразность замены сложения умножением, познакомить со знаком умножения (х, •) и с записью действия в строчку. В качестве наглядных пособий используются предметные множества и картинки с изображением предметов, объединенных в равные группы (рис. 12).
Например: «Пересчитайте варежки, связанные парами». Дети считают по 2: 2, 4, б, 8, 10 (рис. 13). Учитель спрашивает, сколько варежек связано вместе. Запишем так, как считали: 2+2+2+2+2 = 10. Сколько пар варежек? (Пять.) Сколько всего варежек? (Десять.) В этом примере сложение можно заменить другим действием — умножением и записать пример короче. Ска-
165
Рис. 12
зать можно так: «По 2 взять 5 раз, получится 10, а записать т.:к 2-5=10».
Так же ведется счет парами, например, вишенок, нарисованных парами на карточках; результат счета записывается сначала ело жением, а потом умножением:
2+2+2+2=8 2x4=8
Рис. 13
Учитель спрашивает: «Какое число записывается первым при умножении? (Слагаемое). Какое число записывается вторым? (Число 4.) Что оно обозначает?» (Число слагаемых.)
Упражнения в счете двойками, тройками проводятся и на других наглядных пособиях. Производится замена сложения умножением.
Полезны задания с дидактическим материалом: «Взять по 2 кубика 3 раза. Записать это действие сложением, заменить сложение умножением». (2+2+2=6, 2x3=6.)
Необходимо и без дидактического материала произвести замену действия сложения умножением и наоборот: 166
3+3+3+3+3=3x5 2x7=2+2+2+2+2+2+2
это сложение
.)то позволит сделать вывод, что умножение Ьииных слагаемых.
Таблица умножения составляется по постоянному множимому, тапы знакомства с табличным умножением числа 2:
1. Счет предметов по 2 до 20 (каждый ученик ведет счет на
Ьидактическом материале: отсчитывает по 2 желудя, листочка,
(Свадрата и т. д.).
2. Счет изображений предметов по 2 на рисунках или число-
||ых фигурках и составление примеров на сложение.
3. Замена сложения умножением и чтение таблицы умноже-
[ния.
На первом уроке, посвященном этой теме, разбираются примеры:
2+2=4 2+2+2=6 2+2+2+2=8
Здесь число 2 повторяется слагаемым несколько раз. В первой строке число 2 повторяется 2 раза, во второй — 3 раза, в третьей — 4 раза. Рациональнее не записывать каждый раз сумму, состоящую из двух, трех, четырех двоек, а указать, сколько раз надо взять по 2, т. е. заменить сложение одинаковых слагаемых
I умножением.
' Как подвести учащихся к этой мысли, разберем на примере с использованием дидактического материала. Можно взять и веточки, на каждой из которых по 2 листочка. «По скольку листочков на ветке? Сколько раз по 2 листочка? Какие числа складывали? Сколько раз складывали? Сколько получилось? Если по 2 (листочка) взять 4 раза, получится 8 (листочков). Это можно записать так: 2x4=8. Вместо слова «взять» записываем знак х (умножить)».
В целях усвоения и закрепления знаний проводятся упражнения на замену действия сложения умножением и наоборот:
| 2+2+2=2-3; |
2x5=2+2+...
Учащиеся должны уметь проиллюстрировать пример на умножение рисунком, составить по рисункам примеры на сложение и умножение. Затем такую же работу выполнить самостоятельно по индивидуальным карточкам.
167
На следующем уроке составляется таблица сложения. Ок»< ние заменяется умножением числа 2 на числа 5, 6, 7. На трет! уроке составление таблицы умножения числа 2 заканчивает (2x8, 2x9, 2x10). Теперь учащиеся учатся читать приме) «Два умножить на девять» и т. д.
Далее учащиеся упражняются в чтении таблицы умножен! замене умножения сложением равных слагаемых и наоборот, < ставлении рисунков к примерам на умножение. Таблицу умножг ния числа 2 они заучивают наизусть.
У каждого ученика должна быть карточка с таблицей умножг ния числа 2. Все должны знать, что 2 — это слагаемое (если пример на умножение заменяется примером на сложение), а 5 -число слагаемых. Упражнения по замене сложения равных слагас мых умножением и наоборот помогут учащимся осознать значениг 1-го и 2-го множителей. Название компонентов действия умножения при изучении умножения в пределах 20 учитель употребляет в своей речи, но не требует знания их названий от учащихся.
При составлении с учащимися таблицы умножения любого числа и при ее заучивании необходимо обратить их внимание на то, что ответ последующего примера больше предыдущего на столько единиц, сколько их в 1-м множителе (рис. 14).
Учитель спрашивает: «Сколько пар вишен в верхнем ряду? Сколько пар вишен в нижнем ряду? На сколько пар вишен меньше в верхнем ряду, чем в нижнем? Как, не считая вишни в нижнем ряду, узнать, сколько их?»
2+2+2+2=2x4= 8 2+2+2+2+2=2x5=10
|
|
| Рис. 14 |
Во втором случае ответ увеличился на 2, так как добавили две вишни, т. е. еще одну двойку.
168
Рис. 15
Во втором случае ответ увеличился на 2, так как добавили две цини, т. е. еще одну двойку.
Эту закономерность необходимо подчеркивать при заучивании таблицы умножения всех чисел. Это поможет учащимся быстрее пучить таблицу. К тому же, если какой-либо табличный ответ ученик не может вспомнить, но помнит ответ предыдущего или последующего примера, он сможет этим помочь себе.
Для лучшего осознания смысла умножения, а также для запоминания таблицы полезны такие упражнения:
1) Составить по рисунку 15 примеры.
2) Вставить нужные числа:
| ПхП=8 |
| 2хП=6 |
| 2х2=П |
Пх6=12
Чтобы учащиеся научились дифференцировать действия сложения и умножения, полезно предлагать такие упражнения:
1) 2+2+2+2=8. Можно ли в этом случае сложение заменить
умножением? Почему?
2+1+2+3=8. Можно ли в этом случае сложение заменить умножением? Почему?
2) Рассмотреть рисунок 15 и вставить нужные знаки.
Подобные упражнения заставляют умственно отсталых учащихся понять, что не во всех случаях сложение можно заменить умножением, осознать, что умножение — это сложение одинаковых слагаемых. Подобные упражнения имеют не только обучающее и развивающее, но и коррекционное значение.
С умножением чисел 3, 4, 5 в пределах 20 учащиеся знакомятся аналогично, опираясь на счет предметов (их изображений) равными группами. Составляются таблицы сложения равных чисел. Сложение равных чисел заменяется умножением.
Но уже при изучении таблицы умножения числа 3 нужно обратить внимание на то, что в изученных таблицах есть примеры с одинаковыми ответами. Учащиеся должны сами отыскать примеры с одинаковыми ответами на индивидуальных карточках, обвести их цветными карандашами одного цвета. Учитель предлагает
169
|
|
выписать первую пару примеров (2x3=6, 3x2=6) и сравнить ставя перед учащимися такие вопросы: «Какой ответ в пример. Какие числа умножали? Какое число умножают в первом прт ре? (То же во втором.) На какое число умножают в перв< примере? (То же во втором.) В чем сходство этих примеров? I1. чем их различие?»
Чтобы сделать вывод о переместительном свойстве умножении, ограничиться рассмотрением только примеров нельзя. Это свойп во вводится после рассмотрения ряда рисунков с изображение v предметов или самих предметов и подсчета их общего количесть т. е. с помощью широкого применения дидактического материал Учитель просит всех учеников взять по 2 палочки 3 раз. положить их парами и сказать, сколько всего палочек. Каком пример на умножение можно составить? (2x3=6.)
|
|
Затем он просит взять по 3 палочки 2 раза, положить их пи три и сказать, сколько палочек всего, какой пример на умножение можно составить, изменилось ли количество палочек. Рассмотрим рисунок 16 и ответим на вопросы: Сколько яблок в ряду? Сколько рядов по 2 яблока?
Сколько всего яблок? Как записать? (2x3=6.)
Сколько яблок в столбце? Сколько столбцов по 3 яблока?
Сколько всего яблок? Как записать? (3x2=6).
Изменилось ли количество яблок, когда считали их по 2, а потом по 3?
| Рис. 16 |
Значит, 2x3=3x2, т. е. от перестановки чисел (множителей) в примерах на умножение ответ (произведение) не изменится. Учитель в своей речи употребляет слова множители, произведение.
Путем замены действия умножения сложением следует еще раз показать учащимся, что результаты при вычислении остаются равными:
2-3=2+2+2=6 3-2=3+3=6
Рассмотрения только одного случая недостаточно, чтобы сделать вывод о переместительном свойстве умножения. 170
Надо показать учащимся, что подобные рассуждения можно провести для любых двух
О^-^ чисел, но взять уже не те примеры, в кото-
Г } рых они подметили одинаковые ответы, а
^_^^ любые другие. Например, можно сделать к
Г ) С \ примеру 3-5=15 рисунок (рис. 17). ^— —^ Сначала считаем по 3 кружочка, располо-
О/"\ женных в 5 рядов. Всего 15 кружочков.
V__ / Затем считаем по 5 кружочков, расположен-
*х~ч /—ч /—ч ных в 3 столбца, всего тоже 15 кружков. () () () Значит, 3-5=5.3.
На этих фактах отдельные учащиеся могут
рис 17 самостоятельно сделать вывод: от перемены
мест множителей произведение не меняется. Для того чтобы, применяя этот закон, учащиеся не оторвались от его наглядной основы, можно время от времени предлагать им составлять рисунок, на котором удобно показать сущность пере-местительного закона умножения.
В дальнейшем, при составлении последующих таблиц умножения, учитель опирается не только на счет равными группами предметов, равными числами и на составление таблицы сложения, но и на переместительный закон умножения.
ОБУЧЕНИЕ ТАБЛИЧНОМУ ДЕЛЕНИЮ В ПРЕДЕЛАХ 20
;• '^
В школе VIII вида действие деления рассматривается независимо от действия умножения. Только тогда, когда дети хорошо усвоят сущность деления, деление сопоставляется с умножением, устанавливается взаимосвязь между этими двумя действиями. Опыт показывает, что вывод деления из умножения без объяснения сущности самого процесса деления оказывается непонятным умственно отсталым учащимся.
Известно, что существует два вида деления: деление на рав ные части и деление по содержанию. Встает вопрос, с каким видом деления раньше знакомить учащихся школы VIII вида.
В практике обучения математике школьников с нарушением интеллекта сложилась традиция начинать изучение действия деления с деления на равные части. Учащиеся на конкретном материале (операции над предметными множествами) знакомятся с делением на равные части.
171
Действия умножение и деление изучаются параллельно, т после изучения умножения числа 2 изучается деление на 2 ные части, эти два действия сопоставляются, устанавливав связь между ними. Далее изучается умножение числа 3 в пр< лах 20 и соответствующие ему случаи деления на 3 равные ча и т. д. Случаи деления на 5, б, 7, 8, 9 даются на основе уста? ления взаимосвязи деления с умножением. (Это операция нах дения одного из множителей по известному произведению и др\ тому множителю.)
После изучения деления на равные части (все случаи — 3 и класс) учащиеся знакомятся с' делением по содержанию при решг нии задач (3-й класс). В конкретных жизненных ситуациях и с помощью решения задач показывают сходство и различие двух видов деления>1 —,•»
Смысл действия деления на равные части может быть понят умственно отсталыми школьниками только на операциях с пред метными множествами. Каждый ученик должен неоднократно не только наблюдать, но и самостоятельно проделывать операцию деления на равные части элементов различных предметных множеств. Сначала работа проводится на предметах, трафаретках, а затем и на изображениях предметов (в виде рисунков), на аппликациях и т. д. У каждого ученика должен быть счетный ящик или конверт с предметами и их изображениями.
Учитель создает определенную жизненную ситуацию: «Мама принесла из магазина 4 апельсина. У мамы двое детей — Коля и Саша. Она отдала апельсины Коле и предложила разделить их между двумя мальчиками. Как Коля разделил апельсины?»
К доске учитель вызывает двух учеников. Один из них делит апельсины. Выясняется, что разделить апельсины на две группы можно по-разному: можно дать Коле 1 апельсин, а Саше 3; можно дать Саше 1 апельсин, а Коле 3; можно Коле и Саше дать по 2 апельсина, т. е. разделить апельсины поровну на две части.
Далее учитель предлагает разложить (разделить) б карандашей поровну в два стаканчика и показывает, что делить нужно по одному: один карандаш положить в первый стаканчик, один — во второй и т. д. Делить надо до тех пор, пока не останется ни одного карандаша.
В процессе деления на равные части конкретных предметов мы сознательно рекомендуем исключить одну операцию — отобрать сразу количество предметов, соответствующее числу равных час-172
на которое делится множество предметов. Операция мыслен-установления взаимно однозначного соответствия между чис-предметов, которые надо сразу взять, и числом частей, на 1орые делится число, чрезвычайно затрудняет процесс деления ||>| равные части даже предметных совокупностей.
Диалогично показываем практически деление на 3, 4, 5 равных |1п> к'й (поровну), а каждый учащийся повторяет деление на рав-части в работе на партах. Учащиеся при делении конкрет-|и.|'. предметов записывают примеры в тетради с помощью цифр и |>пфметических знаков. Вводится знак (:) и запись действия деле-Цпм 4:2=2, 6:2=3, 8:4=2, 10:5=2.
Дети учатся читать и записывать эти действия.
После общего ознакомления с действиями умножения и деленном на равные части можно переходить к составлению таблиц умножения и деления, начиная с таблицы умножения числа 2, а потом деления на две равные части и т. д.
2:2 = 1. Рассуждения проводятся так: «Возьмем два яблока. Разделим их поровну на два — разложим поровну в две вазы. Смотрите, как нужно делить. Одно яблоко кладем в первую вазу, одно — во вторую. Все ли яблоки разделили (разложили)? Сколько яблок в каждой вазе?» Подойти к записи можно так: «Сколько было яблок? (2.) Запишем число 2. Что делали с яблоками? (Делили.) Слово разделить обозначается «:» (две точки, которые ставятся одна под другой). На сколько равных частей делили? (На две равные части.) Запишем число 2. Сколько получили? (По одному.) Запись 2:2 = 1 читать нужно так: два разделить на две равные части, получится по одному».
Учащимся предлагается отсчитать по два кружочка и разделить их на две равные части (разложить на наборном полотне, положить на два квадрата разного цвета).
В тетрадях ученики рисуют два кружочка и делят их на две равные части вертикальной прямой. (Делают это учащиеся по образцу, данному на доске.) Записывают пример 2:2 = 1.
Затем делят 4 предмета на две равные части и записывают: 4:2=2. После составления таблицы деления на две равные части учащиеся приобретут некоторый навык деления на равные части (по одному). При ознакомлении с делением на три равные части учитель показывает, что из всех предметов, которые делим, надо взять 3 предмета и делить, раскладывая их, например, в стаканчики по одному. Так составляются таблицы деления на три, четыре,
173
пять равных частей в пределах 20. Каждый пример таблицы дс.. ния сопоставляется с соответствующим примером таблицы ум г жения и устанавливается их взаимосвязь. Самостоятельно эт взаимосвязи умственно отсталые дети установить не могут. Так сопоставление поможет учащимся заучить таблицу умножения деления.
ОБУЧЕНИЕ ТАБЛИЧНОМУ УМНОЖЕНИЮ В ПРЕДЕЛАХ 100
В 3-м классе повторяется табличное умножение в пределах 1'0 и заканчивается изучение всего табличного умножения и делении По-прежнему много внимания уделяется наглядной основе и счету равными группами и числами. Однако результат умножения к примерах, где второй множитель меньше первого (например, 6x2, 6x3, 6x4, 6x5), надо записывать на основе знания учащимися переместительного закона умножения. Составив ответы, обяза тельно надо дать на замену действия умножения сложением ран ных слагаемых. Ответы от сложения соответствующих им приме ров на умножение сравниваются. Время от времени можно пред лагать учащимся составить рисунок к примеру на умножение.
Надо добиваться того, чтобы ученики могли получить забытый ответ к примеру на умножение, заменив умножение сложением равных слагаемых или прибавив к известному предыдущему ответу число, которое умножаем. Так, если ученику дан пример 6x9 и он забыл ответ, однако помнит, что 6x6=36, тогда к 36 он прибавляет по 6: 36+6=42 (это 6x7), 42+6=48 (это 6x8), 48+6=54 (это 6x9); значит, 6x9=54.
Приведем фрагмент урока, на котором учащиеся знакомятся с таблицей умножения числа 6.
«Посчитаем шестерками до 60 в прямом порядке. Посчитаем, отсчитаем от 60 по 6.
Знаете ли вы, что посуду группируют в сервизы по 6 предметов? Например, столовый сервиз состоит из 6 глубоких тарелок, 6 мелких больших и 6 мелких маленьких тарелок. Так же продают наборы столовых приборов: 6 ножей, 6 вилок, 6 ложек. Сколько в столовом сервизе тарелок, если в нем 6 тарелок больших и 6 маленьких? (Показ рисунка с тарелками по 6 в ряд.) Каким действием это можно узнать? (6+6=12.)
Вспомним, сколько будет, если 3x6. Поменяем местами сомножители: 6x3=18.
174
I Продолжим составление таблицы дальше: 6x4? Как можно Лиги ответ к этому примеру? Поменяем местами множители: iv I, =24, значит, 6x4=24. Проверим, правильно ли мы нашли и* I. Каким действием можно заменить умножение? Запишем:
• I =6+6+6+6=24.
| I |
Решим пример 6x5 сначала перестановкой сомножителей: К 5=5x6, 5x6=30, значит, 6x5=30. Заменим действие умно-гния сложением: 6x5=6+6+6+6+6=30». I Па фрагменте данного урока показано, как переместительный 1кон умножения использовался при знакомстве учащихся с новы-|И случаями умножения.
В тех случаях, когда второй множитель равен или больше _ервого (6x6, 6x7, 6x8, 6x9, 6x10), для нахождения ответов |ельзя использовать прием, основанный на знании переместитель-,р1ого закона умножения. Ответ отыскивается с помощью составления таблицы сложения равных слагаемых с опорой на счет равных групп предметов: |6x6=36
6X7=42 6X8=48 6X9=54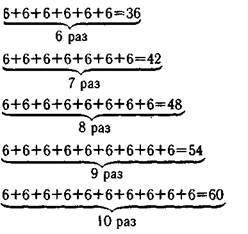 
6X10=60
С распределительным законом умножения учащиеся школы VIII вида не знакомятся.
Учитель должен обратить внимание на то, что ответ каждого последующего примера может быть получен из предыдущего путем прибавления 6 (единиц множимого).
При составлении таблиц умножения учим учащихся опираться на использование переместительного свойства умножения, а также на наблюдение за изменением произведений в строчках таблиц умножения: произведение, полученное в последующей
175
строчке (например, 5x6=30) равно произведению в предыдумн1 строчке (5x5=25) плюс число, которое умножается (5). Прош можно произведение двух чисел записать в обобщенном виде:
ахЬ=л-'(Ь-1)+а.
С помощью вышеназванных свойств табличного умножения со ставляются таблицы умножения чисел 7, 8, 9.