Задание 4 «Пересечение поверхностей»
Содержание задания
Задание состоит из двух задач.
Задача 1
Построить линию пересечения призмы и сферы.
Задача 2
Построить линию пересечения двух цилиндров.
Графическая работа выполняется на двух форматах А3. Задача решается в трех проекциях. Варианты задач даны в таблицах 5,6. Размеры на чертежах не проставляются. Перед выполнением задания необходимо изучить теоретический материал по заданной теме и ответить на контрольные вопросы.
Секущие плоскости и линии проекционной связи проводятся тонкими сплошными линиями. При вычерчивании проекций геометрические тела считать непрозрачными. Линии определяющие полный очерк геометрической поверхности в местах наложения проекций показывать сплошной тонкой линией. Плоскости следует обозначать прописными буквами греческого алфавита, точки пересечения линий – арабскими цифрами. При решении задач проводят большое количество секущих плоскостей для более точного построения линии пересечения, но при окончательной обводке чертежа рекомендуется сохранить лишь те, которые определяют опорные точки и несколько промежуточных. Для этих точек на чертеже должны быть сохранены и линии проекционной связи.
В графе 1 основной надписи чертежа записывается шифр ИГ00. 01.5. 01.00.001 (где 01-номер варианта, 001-три последние цифры в зачетке).
На рисунках 10,11,12,13 приведены примеры выполнения и оформления задания 4.
Алгоритм решения
Задача 1
Плоскость каждой грани призмы в пересечении с поверхностью сферы дает свой тип линий - это будут участки плоских кривых второго порядка (эллипса и окружности). Эти три кривые соединяются между собой в замкнутую кривую.
Для построения линии пересечения используется метод секущих плоскостей. В качестве секущих плоскостей используются фронтальные плоскости уровня (Ф1, Ф2…). Эти плоскости в пересечении с призмой дают прямоугольники, а со сферой - окружности. В пересечении окружностей с соответствующими прямоугольниками получаем точки искомой линии пересечения.
Следует учесть, что если в пересечении участвует проецирующая поверхность (призма или цилиндр), то линия пересечения на одной из проекций известна сразу: она совпадает с проекцией основания проецирующей поверхности. В данном примере горизонтальная проекция линии пересечения совпадает с горизонтальной проекцией очерка основания призмы.
1.Построение начинаем с обозначения характерных (опорных) точек линии пересечения. В первую очередь определяем точки пересечения ребер призмы с поверхностью сферы (1), затем точки пересечения очерковых образующих сферы с гранями призмы (3,6).
2. Определяем количество и место положения промежуточных точек. Число промежуточных точек должно быть достаточным для точного построения эллипсов. Для построения окружности промежуточные точки не требуются. Чтобы не загромождать чертеж, промежуточные точки допускается цифрами не обозначать.
3. Находим фронтальные проекции выбранных точек. Для нахождения фронтальной проекции точки 1 вводим секущую плоскость Ф (Ф1), которая рассекает сферу по окружности радиуса R. Горизонтальная проекция окружности совпадает с линией плоскости, на фронтальной плоскости проекций окружность проецируется в натуральную величину. В пересечении этой окружности с ребром А получаем фронтальную проекцию точки 1 (12). Аналогичным образом строим все остальные точки, последовательно вводя плоскости Ф,Ф1…
4. По двум имеющимся проекциям точек строим их профильные проекции, последовательно соединив которые, получим профильную проекцию линии пересечения.
5. Видимость линии пересечения на фронтальной плоскости проекций определяем по сфере, т.е. линия пересечения, лежащая в видимой части сферы (части эллипсов) будут видны, а часть эллипсов и окружность, принадлежащая грани АВ не видны и изображаются линией невидимого контура. Обводим очерки поверхностей. У призмы ребро С(С2) полностью видимое, а ребра А(А2) и В(В2) видны соответственно до точек 1(12). Очерковый главный меридиан сферы обводим линией видимого контура до точки 3 (32).
6. Определяем видимость линии пресечения на профильной плоскости проекций.
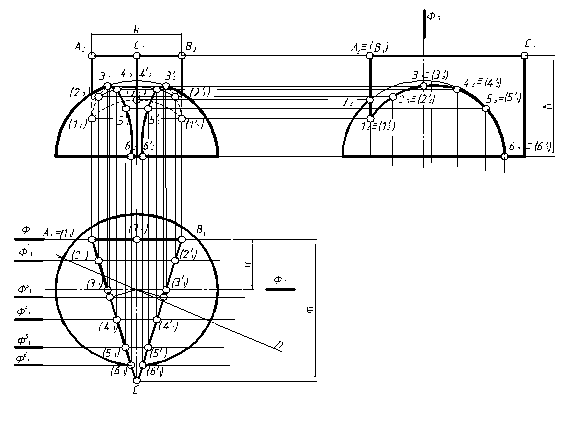
Рисунок 10- Пример решения задачи 1 задания 4
Таблица 5 –Варианты задачи 1 задания 4
| № варианта | D | n | m | k | h |
| 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 80 | 30 | 70 | 60 | 60 |
| Продолжение таблицы 5 | |||||
| 1 | 2 | 3 | 4 | 5 | 6 |
| 2 | 90 | 45 | 85 | 70 | 65 |
| 3 | 95 | 35 | 90 | 50 | 70 |
| 4 | 85 | 30 | 88 | 60 | 65 |
| 5 | 92 | 50 | 46 | 100 | 60 |
| 6 | 88 | 28 | 80 | 70 | 60 |
| 7 | 86 | 30 | 80 | 60 | 60 |
| 8 | 90 | 35 | 35 | 80 | 65 |
| 9 | 92 | 32 | 90 | 60 | 65 |
| 10 | 85 | 30 | 55 | 70 | 65 |
| 11 | 80 | 35 | 80 | 60 | 65 |
| 12 | 90 | 45 | 95 | 70 | 60 |
| 13 | 85 | 35 | 80 | 40 | 65 |
| 14 | 80 | 40 | 80 | 50 | 62 |
| 15 | 86 | 36 | 70 | 96 | 70 |
| 16 | 82 | 32 | 82 | 68 | 64 |
| 17 | 90 | 40 | 90 | 80 | 68 |
| 18 | 88 | 40 | 80 | 50 | 70 |
| 19 | 86 | 0 | 43 | 96 | 65 |
| 20 | 80 | 30 | 40 | 90 | 60 |
| 21 | 90 | 30 | 80 | 80 | 65 |
| 22 | 92 | 0 | 60 | 92 | 68 |
| 23 | 88 | 30 | 100 | 35 | 62 |
| 24 | 85 | 35 | 80 | 40 | 60 |
| 25 | 80 | 30 | 90 | 90 | 64 |
| 26 | 84 | 25 | 80 | 40 | 60 |
| 27 | 86 | 44 | 94 | 60 | 55 |
| 28 | 88 | 40 | 84 | 70 | 65 |
| 29 | 90 | 0 | 45 | 90 | 65 |
| 30 | 85 | 35 | 70 | 100 | 65 |
Задача 2
Линия пересечения двух цилиндров - пространственная кривая. Цилиндры - это проецирующие поверхности, один из них занимает горизонтально проецирующие положение, другой профильно проецирующее, таким образом положение линии пересечения на П1 и П3 известно сразу и совпадает с очерками оснований этих цилиндров.
1. Построение начинаем с обозначения характерных (опорных) точек линии пересечения. В первую очередь определяем точки пересечения очерков пересекающихся поверхностей, точки 1 и 4, которые так же будут являться точками перемены видимости на плоскостях проекций.
2. Так как цилиндры проецируются перпендикулярно горизонтальной и профильной плоскостям проекций - точки их пересечения совпадают с проекциями цилиндров на этих плоскостях. Выбираем промежуточные точки произвольно, на равном расстоянии друг от друга по окружности на горизонтальной плоскости. Определяем проекции этих точек на профильной плоскости проекций, используя базовую плоскость – фронтальную плоскость уровня.
3. Находим фронтальные проекции точек линии пересечения. Для этого проводим горизонтальные и вертикальные линии связи, на пересечении которых получим искомые проекции точек линии пересечения двух цилиндров на фронтальной плоскости проекций. Соединяем полученные точки лекальной кривой.
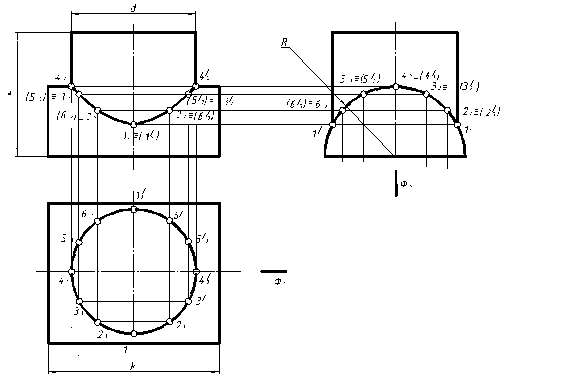
Рисунок 11-Пример решения задачи 2 задания 4
Таблица 6- Варианты задачи 2 задания 4
| № варианта | R | d | h | k |
| 1 | 45 | 80 | 80 | 110 |
| 2 | 40 | 90 | 85 | 105 |
| 3 | 42 | 88 | 85 | 105 |
| 4 | 45 | 85 | 85 | 110 |
| 5 | 42 | 95 | 86 | 115 |
| 6 | 40 | 45 | 80 | 105 |
| 7 | 45 | 80 | 85 | 110 |
| 8 | 44 | 94 | 90 | 105 |
| 9 | 40 | 45 | 90 | 108 |
| 10 | 45 | 85 | 88 | 100 |
| 11 | 40 | 90 | 80 | 105 |
| 12 | 45 | 90 | 94 | 110 |
| 13 | 45 | 80 | 90 | 105 |
| 14 | 35 | 80 | 80 | 100 |
| 15 | 44 | 95 | 90 | 115 |
| 16 | 45 | 85 | 85 | 105 |
| 17 | 40 | 90 | 85 | 100 |
| 18 | 42 | 90 | 88 | 115 |
| 19 | 45 | 85 | 86 | 110 |
| 20 | 35 | 80 | 88 | 100 |
| 21 | 40 | 85 | 80 | 115 |
| 22 | 45 | 85 | 85 | 110 |
| 23 | 40 | 88 | 95 | 110 |
| 24 | 44 | 95 | 85 | 115 |
| 25 | 45 | 80 | 90 | 105 |
| 26 | 35 | 80 | 85 | 100 |
| 27 | 40 | 80 | 90 | 105 |
| 28 | 45 | 85 | 88 | 110 |
| 29 | 35 | 75 | 85 | 100 |
| 30 | 42 | 88 | 84 | 110 |
Контрольные вопросы
1. Сформулируйте правило построения линии взаимного пересечения поверхностей многогранников.
2. Сформулируйте правило построения линии взаимного пересечения многогранника с поверхностью вращения.
3. Сформулируйте правило построения линии взаимного пересечения поверхностей вращения.
4. Сущность метода вспомогательных плоскостей.
Библиографический список
1 ЕСКД. Общие правила выполнения чертежей : сб. [Текст] / - М.: Изд-во стандартов, 1991.-160 с.
2. Буланже, Г.В. Инженерная графика. Проецирование геометрических тел
[Текст] / Г.В.Буланже, И.А. Гущин, В.А. Гончарова-М.: Высш. шк., 2003.-184 с.
3. Боголюбов, С.К. Индивидуальные задания по курсу черчения [Текст] / С. К. Боголюбов - М.: Высш. шк., 2004.- 368 с.
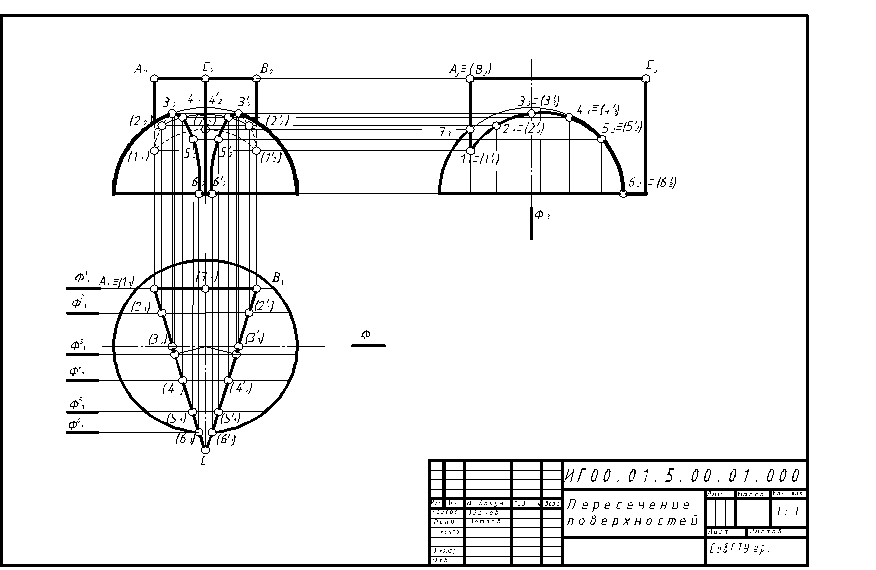
Рисунок 12 -Образец выполнения задачи 1 задания 4
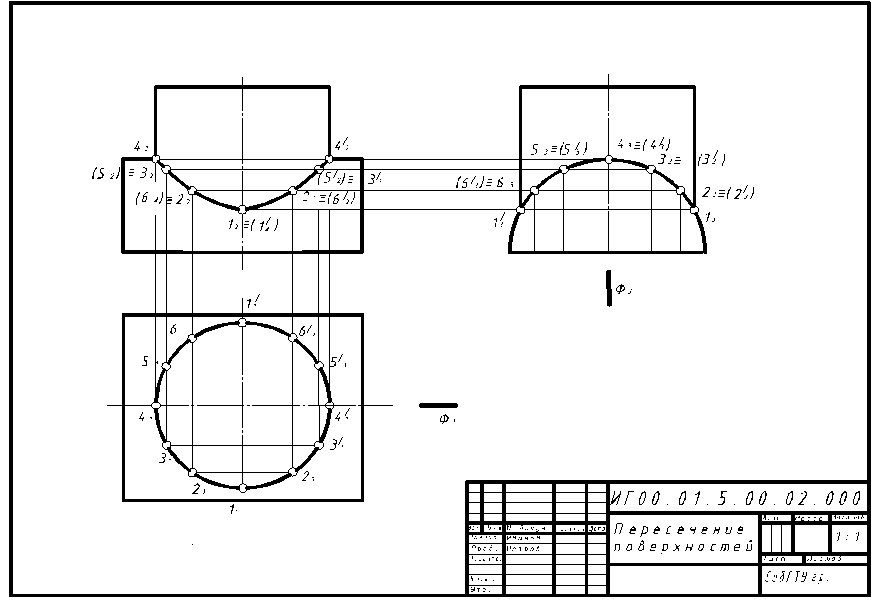
Рисунок 13-Образец выполнения задачи 2 задания 4
Приложение А
(справочное)
Перечень ключевых слов
алгоритм парабола
видимость элементов пересечение
взаимное положение перпендикулярность
вращение плоскости проекций
гипербола поверхность
горизонталь призма
комплексный чертеж развертка
линии уровня сечения
масштаб способы проецирования
меридиан параллельность
методы преобразования способ прямоугольного
комплексного чертежа треугольника
метод замены сфера
плоскостей проекций точки (конкурирующие,
метод вращения опорные, характерные)
многогранники фигура сечения
направление взгляда цилиндр
натуральная величина экватор
ось проекций эпюр Монжа
отрезок очерк
Приложение Б
(справочное)
Обозначения и условности в тексте и на чертежах
А, В, С … или 1, 2, 3… - точки в пространстве обозначаются прописными буквами латинского алфавита;
а, в, с… - линии (прямые и кривые) в пространстве – строчными буквами латинского алфавита;
h – горизонтальная, f – фронтальная, p – профильная прямые уровня;
Г – горизонтальная, Ф – фронтальная, Y - профильная плоскости уровня, S - проецирующие плоскости в пространстве обозначаются прописными буквами греческого алфавита;
a, b,g - углы в пространстве – строчными буквами греческого алфавита;
П – плоскости в поле проекций – прописной греческой буквой с подстрочным индексом: П1 – горизонтальная, П2 – фронтальная, П3 – профильная плоскости проекций. Остальные плоскости проекций – П4, П5, П6… Пn.
А¢, А¢¢, а¢, а¢¢, S¢, S¢¢ - последовательность геометрических элементов в пространстве – теми же буквами, но с надстрочными индексами. Проекции точек, линий, плоскостей, поверхностей, углов на комплексном чертеже обозначаются теми же буквами, что и в пространстве, но с добавлением подстрочного индекса 1, 2, 3, 4 …n, соответствующего плоскости проекций: на плоскости П1 – А1; П2 – А2; П3 – А3 … Пn – Аn.
А°, а° – не проекционные элементы на комплексном чертеже – теми же буквами, но с надстрочным индексом ноль.
x, y, z, s – оси проекций в пространстве;
`А, `S, `а – новые положения геометрических элементов после вращения или параллельного перемещения – теми же буквами, но с одной чертой наверху после первого вращения, с двумя после второго.
Обозначение отношений между геометрическими элементами:
= или º совпадают, результат действия, равны;
// - параллельны;
^ - перпендикулярны;
°/ - скрещиваются;
Î - принадлежит, является элементом;
Ì - включает, содержит;
È - объединение;
Ç - пересечение.
Приложение В
(справочное)








