Задание 3 «Сечение поверхностей плоскостями»
Содержание задания
Задание состоит из двух задач.
Задача 1
Построить три проекции пирамиды с призматическим вырезом.
Задача 2
Построить три проекции прямого кругового конуса с призматическим вырезом.
Графическая работа выполняется на одном формате А3.. Варианты задач даны в таблицах 3,4. Размеры на чертежах не проставляются. Перед выполнением задания необходимо изучить теоретический материал по заданной теме и ответить на контрольные вопросы. В графе 1 основной надписи чертежа записывается шифр ИГ00. 01.4. 01.00.001 (где 01-номер варианта, 001-три последние цифры в зачетке).
На рисунках 6,7,8,9 приведены примеры выполнения и оформления задания.
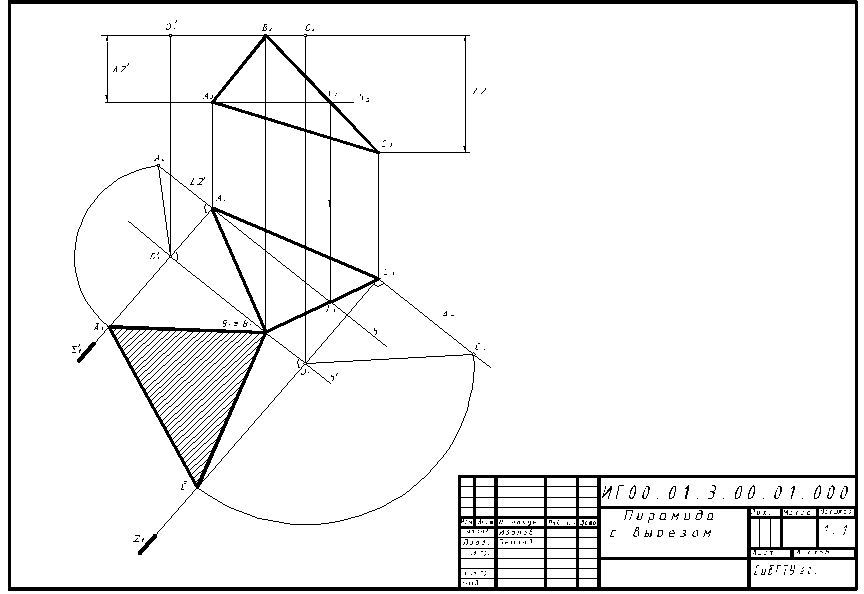
Рисунок 5-Образец выполнения задания 2
Алгоритм решения
Задача 1
1. Cтроим три проекции пирамиды в тонких линиях.
2. Определяем каким количеством секущих плоскостей образован вырез. В данном примере вырез образован тремя секущими плоскостями, которые в пересечении с пирамидой дают ломаные линии.
3. Определяем характерные точки - точки пересечения секущих плоскостей с ребрами пирамиды 1(12), 2(22), 3(32), 4(42), 7(72), 8(82); линию пересечения плоскостей между собой 5(52), 6(62).
4. Находим горизонтальные проекции точек 1(11)и 2(21) по линиям связи, а точек 3(31), 4(41), 5(51), 6(61), 7(71), 8(81) методом секущих плоскостей.
5. Соединяем последовательно полученные точки с учетом видимости. Т.к. на горизонтальной плоскости проекций видны все точки, лежащие на боковой поверхности пирамиды, то соединяем линией видимого контура точки 2(21)-4(41)-6(61)-8(81)-1(11) и 2(21)-3(31)-5(51)-7(71)-1(11). Между точками 5(51)и 6(61) проводим линию невидимого контура, которая получается в пересечения двух секущих плоскостей. На профильной плоскости проекций видимыми будут все линии пересечения. Линией невидимого контура проводим только часть ребра С.
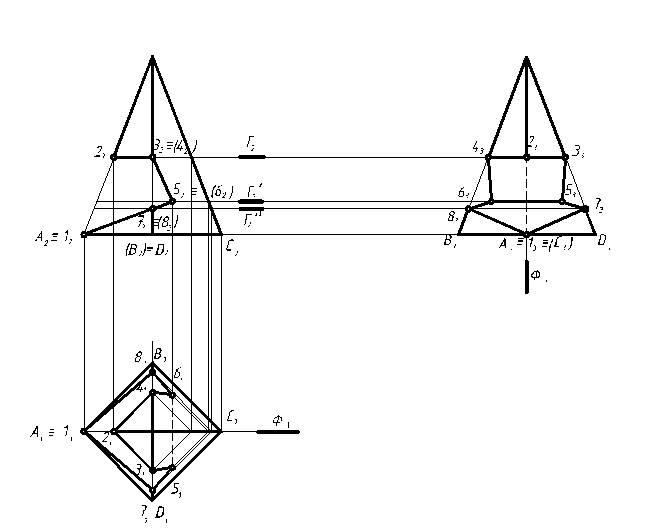
Рисунок 6 –Пример решения задачи 1 задания 3
Задача 2
1. Строим три проекции конуса в тонких линиях.
2. Определяем, каким количеством плоскостей образован вырез, и какая фигура получается в пересечении поверхности с этими плоскостями. В данном примере вырез образован тремя секущими плоскостями, которые в пересечении с конусом образуют гиперболу, окружность и эллипс.
3. Определяем точки пересечения секущих плоскостей с очерковыми образующими и основанием конуса-1(12), 6,7 (62º72),8 (82),13,14 (132º142). Кроме этих точек определяем промежуточные точки для построения гиперболы и эллипса.
4. Находим горизонтальные и профильные проекции названных точек методом секущих плоскостей. В качестве секущих плоскостей используются горизонтальные плоскости уровня (Г2,…). В результате пересечения этих плоскостей с конусом получаются окружности.
5. Соединяем последовательно полученные точки с учетом видимости. Т.к. на горизонтальной проекции видны все точки, лежащие на боковой поверхности конуса, то соединяем линией видимого контура точки 11-31-51-71 и -61-41-21-11 (части эллипса), 71-81-61 (часть окружности), 131-81 и 141-81 (ветви гиперболы). Между точками 6,7 (61,71) проводим линию невидимого контура, которая получается в результате пересечения секущих плоскостей.
6. На профильной плоскости проекций видимыми будут точки 73-53-33-13-23-43-63 (эллипс), 133-143. Линия 73-83-63 , в которую проецируется окружность, а также часть гиперболы от точки 8 (83) к точкам 9 (93) и 10 (103) и дальше проводим линией невидимого контура. Левую и правую образующие конуса обводим сплошной основной линией от вершины до точек 7(73) и 6 (63).
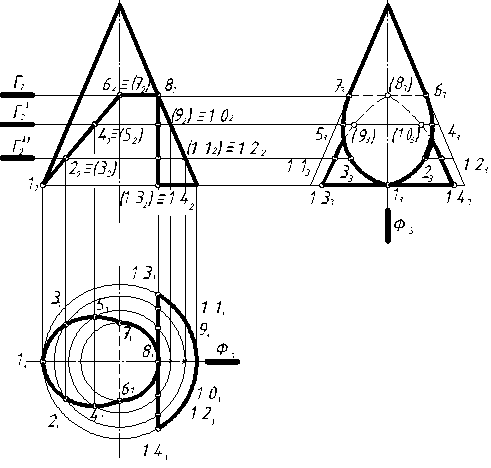
Рисунок 7-Пример решения задачи 2 задания 3
Контрольные вопросы
1.Что называется многогранником?
2 Что является сечением поверхности многогранника плоскостью?
3.Что называется поверхностью вращения?
4. Укажите основные свойства поверхностей вращения?
5. Назовите методы нахождения точек на поверхностях вращения, многогранниках.
6. Какие фигуры могут быть получены при рассечении плоскостью кругового цилиндра, конуса, сферы? В каких случаях эти поверхности рассекутся по графически простым линиям?
7. Что представляет собой вырез? Чем можно задать необходимую форму выреза?
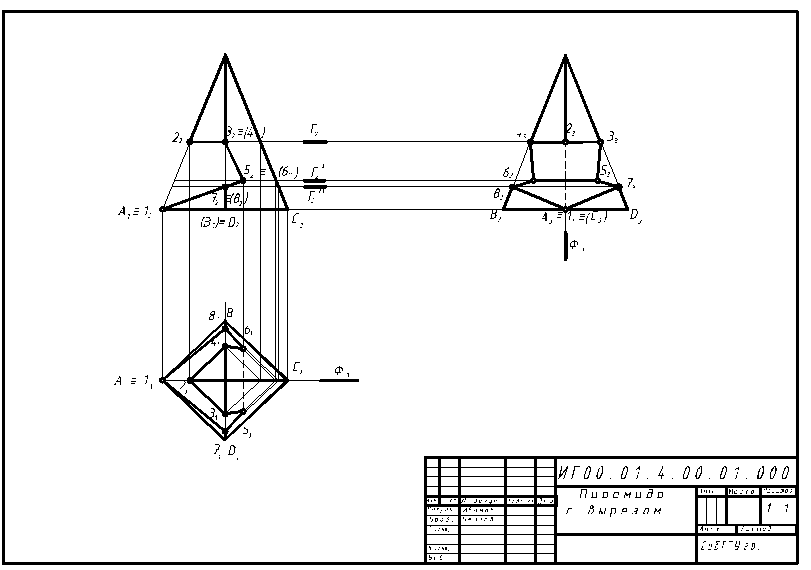
Рисунок 8 Образец выполнения задачи 1 задания 3
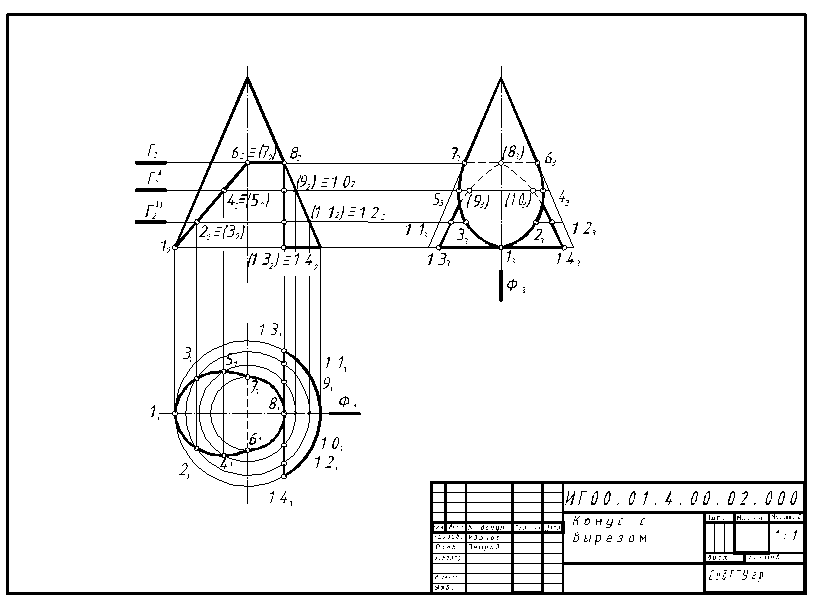
Рисунок 9-Образец выполнения задачи 2 задания 3
Таблица 3-Варианты задачи 1 задания 3
| № варианта | Условие задачи | № варианта | Условие задачи |
| 1 | 2 | 3 | 4 |
| 1 | 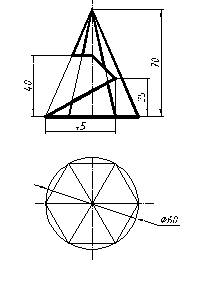
| 4 | 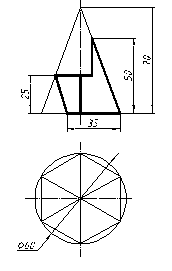
|
| 2 | 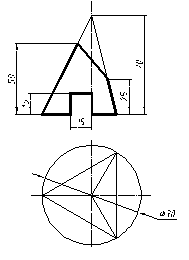
| 5 | 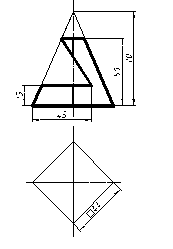
|
| 3 | 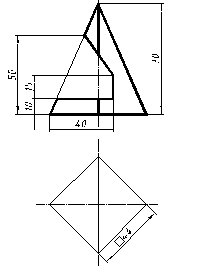
| 6 | 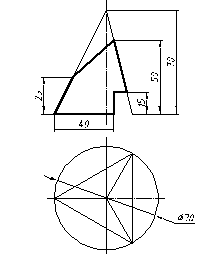
|
Продолжение таблицы 3
| 1 | 2 | 3 | 4 |
| 7 | 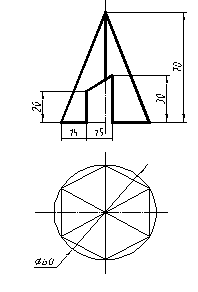
| 10 | 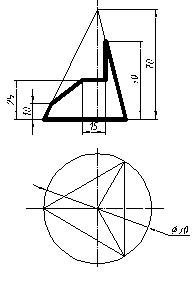
|
| 8 | 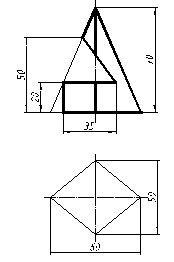
| 11 | 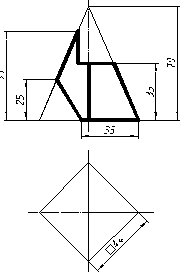
|
| 9 | 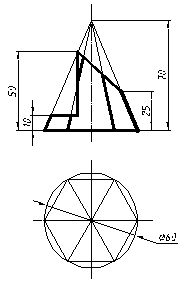
| 12 | 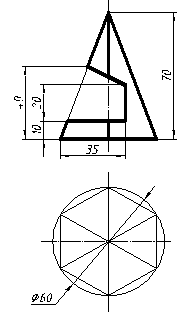
|
Продолжение таблицы 3
| 1 | 2 | 3 | 4 |
| 13 | 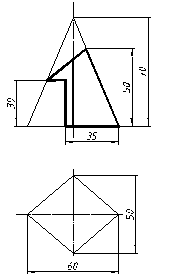
| 16 | 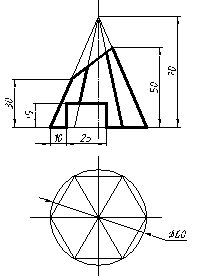
|
| 14 | 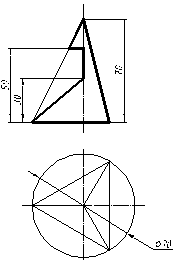
| 17 | 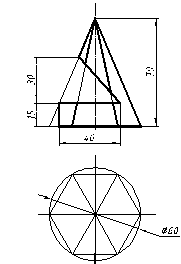
|
| 15 | 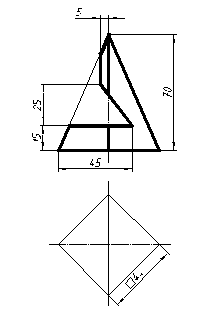
| 18 | 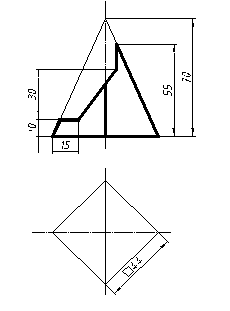
|
Продолжение таблицы 3
| 1 | 2 | 3 | 4 |
| 19 | 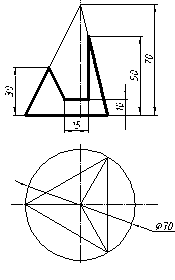
| 22 | 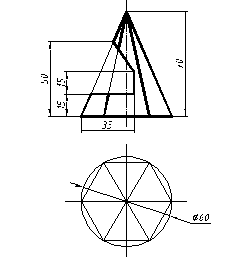
|
| 20 | 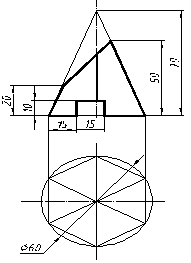
| 23 | 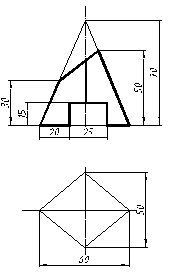
|
| 21 | 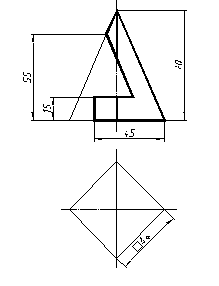
| 24 | 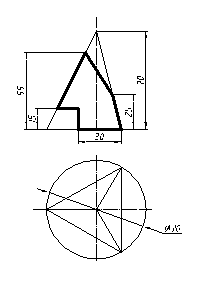
|
Продолжение таблицы 3
| 1 | 2 | 3 | 4 |
| 25 | 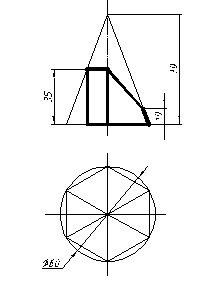
| 28 | 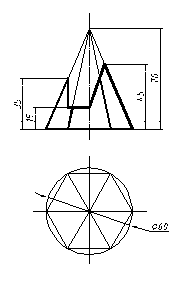
|
| 26 | 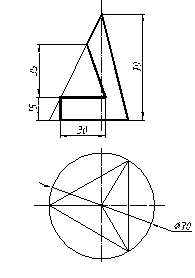
| 29 | 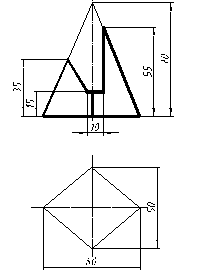
|
| 27 | 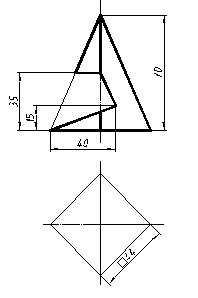
| 30 | 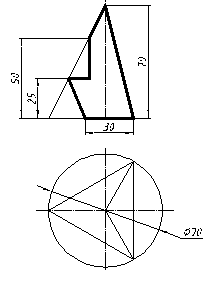
|
Таблица 4- Варианты задачи 2 задания 3
| № варианта | Условие задачи | № варианта | Условие задачи |
| 1 | 2 | 3 | 4 |
| 1 | 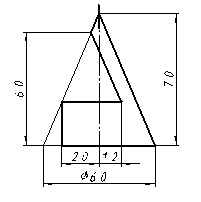
| 5 | 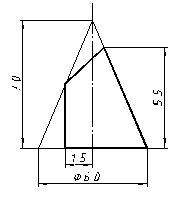
|
| 2 | 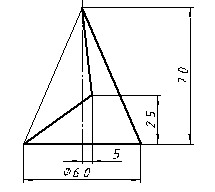
| 6 | 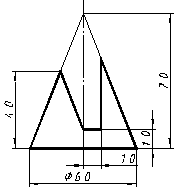
|
| 3 | 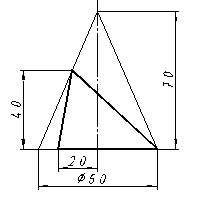
| 7 | 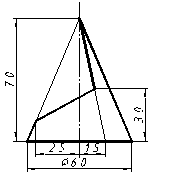
|
| 4 | 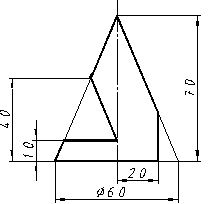
| 8 | 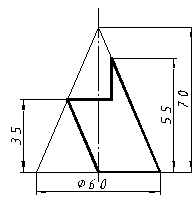
|
Продолжение таблицы 4
| 1 | 2 | 3 | 4 |
| 9 | 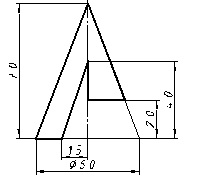
| 13 | 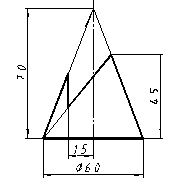
|
| 10 | 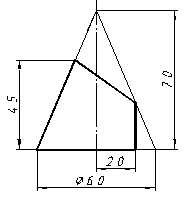
| 14 | 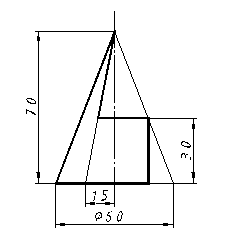
|
| 11 | 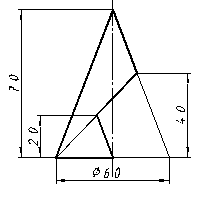
| 15 | 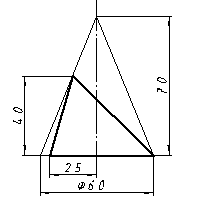
|
| 12 | 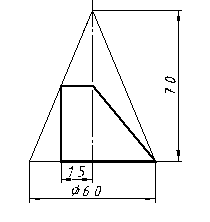
| 16 | 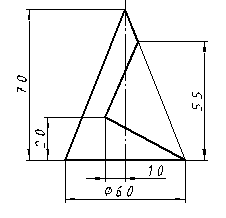
|
Продолжение таблицы 4
| 1 | 2 | 3 | 4 |
| 17 | 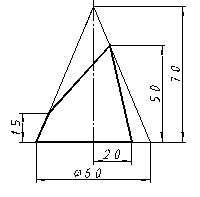
| 21 | 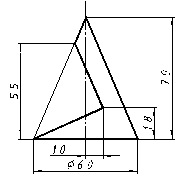
|
| 18 | 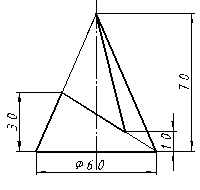
| 22 | 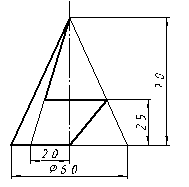
|
| 19 | 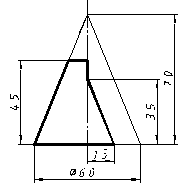
| 23 | 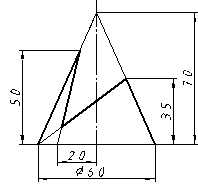
|
| 20 | 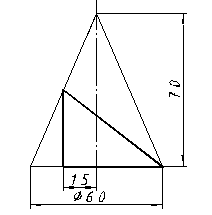
| 24 | 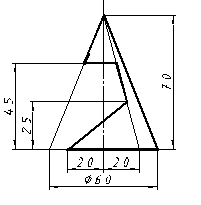
|
Продолжение таблицы 4
| 1 | 2 | 3 | 4 |
| 25 | 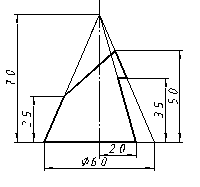
| 28 | 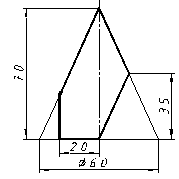
|
| 26 | 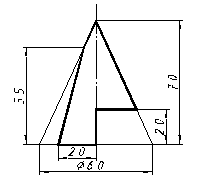
| 29 | 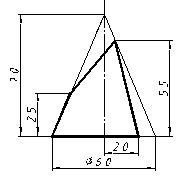
|
| 27 | 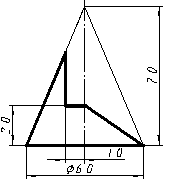
| 30 | 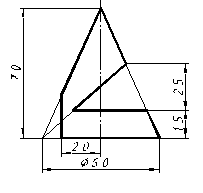
|








